“计数方法”解决问题策略的学习进阶研究

陈瑞华

【摘 要】在澄清知识本质的基础上，基于教学目标细化，从画图、列表、递推推理三个角度对三节“计数方法”课进行解决问题策略的学习进阶比较研究，理解教材编排的意图，提出进一步完善教学的建议。

【关键词】计数方法 解题策略 学习进阶

“计数方法”的学习内容与我们的日常生活密切相关，小学数学中涉及“计数方法”的学习内容有哪些？它解决问题的策略有哪些？笔者拟借鉴国际教育领域中先进的“学习进阶”理论，对北师大版小学数学教材的相关内容进行系统的研究，为进一步优化教学提出合理的建议。

一、教材简介

在北师大版小学数学教材中，涉及“计数方法”的课有三节：三年级上册“搭配中的学问”，四年级上册“数图形的学问”和六年级上册“比赛场次”，它们同属“数学好玩”板块，都是“综合与实践”领域的学习内容。

（一）三年级上册“搭配中的学问”简介

教材创设了搭配服装、营养配餐、去动物园的路线三个具有现实意义的情境，先通过摆一摆、说一说经历有序思考的实践活动，进而引导学生用图、符号表示对象，用连线表示搭配进行有序思考。在此基础上用图、符号、连线方法解决营养配餐问题，进而用符号、连线解决去动物园的路线问题。在实际教学中，学生通常能用加法或乘法表示列举的结果，通过比较三个问题的共性，对解决搭配问题的数学模型有所感悟。

（二）四年级上册“数学图形的学问”简介

教材先引导学生把“鼹鼠钻洞”的实际情境抽象成线段和其上的点，通过有序思考解决问题，并用加法表示结果。菜地旅行引导学生用点表示站点，线段表示路线，借助图形直观引导学生通过有序思考数线段解决单程票的问题。通过站点数递增的练习、递推策略的运用帮助学生感悟数图形中蕴含的规律。

（三）六年级上册“比赛场次”简介

教材呈现10个学生两两比赛的场次安排问题，引导学生通过画图、列表、连线的方法寻找规律，体会“从简单情形开始寻找规律”解决问题的必要性，进而利用这一策略解决问题；借助递推策略感悟蕴含其中的规律；运用“从简单情形开始寻找规律”的策略解决联络方式问题。

二、教学内容的知识背景分析

（一）教学内容的知识背景概述

“计数方法”的基础是所谓的“计数原理”，包括加法原理和乘法原理。加法原理是分类计数，乘法原理是分步计数。

排列组合是组合学最基本的概念，所谓排列，就是指从给定的n个元素中取出m个元素进行排序，计算公式：，是乘法原 理的直接应用。组合则是指从给定的n个元素中取出指定m個元素，不考虑排序，计算公式：。即先计算排列，再除掉重复计数。

（二）教学内容的知识背景分析

1.“搭配中的学问”与“乘法原理”

“搭配中的学问”本质上是“乘法原理”。以教材搭配服饰为例，第一步选帽子，有2种选法；第二步选裤子，有3种选法，一共有2×3种方法，也可以用加法或乘法表示搭配结果，即3+3、2+2+2或2×3，但教材中这样的列式是基于加法和乘法的运算意义的，并没有进行“加法原理”“乘法原理”抽象。

2.“数图形的学问”与“排列”

“鼹鼠钻洞”问题与通常的“数线段”问题有着本质的不同。“数线段”问题本质上是排列问题，如线段上有5个点（包含两端），两个点确定一条线段，先定一个点有5种方法，再定一个点有4种方法，一共有5×4种方法，即20条线段，由于同一条线段被重复计数，所以实际有20÷2=10条线段。“鼹鼠钻洞”问题虽然也可以用5×4÷2计算，5×4是“往返路线”的种数，“除以2”的原因是问题只要求考虑“单程”计数，但教材中在处理这个问题时只用了有序列举找规律，没有进行“排列”的意义与方法抽象。

3.“比赛场次”与“组合”

“比赛场次”本质是“组合问题”，即从一个集合中取两个元素组合。但教材呈现的处理方式上是用了有序列举的方法寻找规律，基于有序列举的方式让学生进行感受递推的方法，体会“从简单的情形寻找规律”解决问题的策略，并没有进行“组合”的意义与方法抽象。

三、解决问题策略的学习进阶

三节课中涉及的主要解题的策略包括画图、列表格递推推理。

（一）画图策略的学习进阶分析

三节课中画图策略的基本出发点是用点表示集合中的元素，用线表示元素间的关系。

在“搭配中的学问”中，学生运用不同的图形或字母来表示帽子和裤子、用连线表示搭配的方法解决问题；在解决去动物园的路线问题时，也用到了连线画图的方式来解决问题。

在“数图形的学问”中，相对于前一课两个集合间的画图连线解决问题，本课在一个集合的元素间画图连线解决问题——按出发点的不同来计数，相对来说更容易混淆，也更难一些。

在“比赛场次”中学生的画图策略比较多样，包括线段图、连线图等。

综合来看，三个课时在画图这一策略方面存在着明显的学习进阶，从只用一种画图的策略到运用多种画图的策略，是有一定的进阶上升的。

（二）列表策略的学习进阶分析

在“搭配中的学问”内容中，教材没有应用列表的策略来解决问题。

在“数图形的学问”中，教材也没有应用列表的策略解决问题。

但通过列表解决问题的策略在教材中还是有所体现的，如三年级下册的“有趣的推理”中就有相关的内容（见图1）。

“比赛场次”中教材呈现的列表策略就比较多样，既可以在表格中利用示意图的方式寻找规律，也可以在表格中利用连线图的方式寻找规律，还可以在表格中用数线段图的方式来寻找规律。利用从简单情形开始，寻找一般的规律，充分体会递推的必要性。

综合来看，三个课时在列表这一策略上的进阶安排是有所不足的。

（三）“递推推理”策略的学习进阶分析

递推是序列计算中的一种常用算法，是基于前一项的推理答案，结合下一步的推理，得到新的序列答案的过程。“搭配中的学问”并没有出现递推推理，下面着重分析后两节课。

1.“数图形的学问”的递推推理进阶分析

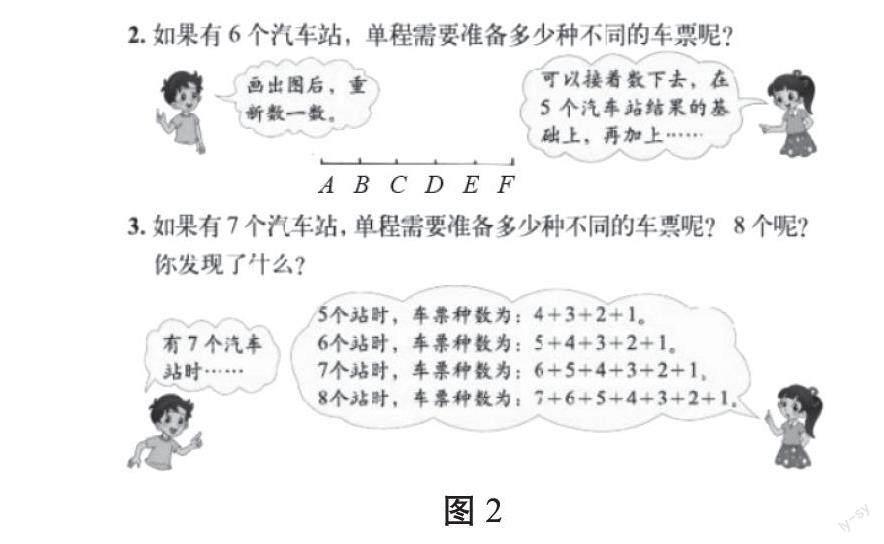
本课学习是学生第一次接触递推推理。教材是在练习中出现递推方法的提示的（见图2）。通过操作，学生发现只要添加新加的这个站点跟原有站点的票数就可以了。

从递推推理的动手操作到算式表示和意义解释是学习的进阶。在解释算式意义的基础上，引导学生寻找站点数与加法中加数的关系，进而对这种关系进行意义解释：每增加一个站点，增加的票数就是站点总数减1，因为新站点与自身不需要票，所以要减1，可利用这种关系列式解决问题。

2.“比赛场次”的递推推理进阶分析

本课的递推推理是借助“退”的策略引出的：解决10个学生比赛场次问题比较复杂，所以要“从简单的开始”思考问题，寻找规律解决问题。递推推理的展开利用了列表、数线段、连线等多种策略，每增加一人比赛，用一个点或增加表格的行和列表示，并用不同颜色的符号标示出来，便于学生清晰地看出递推推理的过程，找出递推推理后一项与前一项的关系。不同于“数图形的学问”中加数依次递减的加法，本课采用了加数依次递增的加法算式，更切合递推推理的特点，意义解释也更为合理。

综合两个课时的教材研究，从“数图形的学问”直接呈现，到“比赛场次”中基于“退”的策略的自主运用，从单一策略到多种策略，从递减算式到递增算式，是一个明显的进阶过程。但是，递推推理从“教”到“用”，间隔两年，后续学习显然难以唤醒以往经验，教师就要联系学生的生活实际展开教学。

四、纵向研究的教学启示与建议

（一）主要解题策略的教学启示与建议

在“搭配的学问”中，教材呈现的解题策略是画图和连线，缺少列表的解题策略，建议增加列表的解题策略，让学生更好地体会乘法原理在搭配问题中的应用。例如，在解决去动物园的路线问题时可以呈现这样的解决方法：从学校到少年宫有A、B两条路，从少年宫到动物园有C、D、E三条路，第一步可以从“列”选，有2种选择，如先选A，第二步选“行”，有3种选择，再选B，重复第二步（见表1）。当然也可以先行后列。这样设计更利于学生感悟乘法原理。

在“数图形的学问”中，教材中呈现的也只有一种解题策略——画线段图，实际上也可以应用列表的策略来解决问题。例如，在一条线段上有A、B、C、D共4个端点，问：一共有多少条线段？由于两个端点决定一条线段，可以列出表2。有序列举分两步：先选一个端点，再选一个端点，A与B组合了，B就不用跟A组合了，由此出现了递减的现象。

从“比赛场次”目前的教学来看，很少有学生采用列表的策略，如果有了前面两节课教学改进的铺垫，采用这一策略的学生人数比例可能会增加。

（二）“递推推理”的教学启示与建议

“搭配的学问”在教材中并没有递推推理的内容，建议安排增加一顶帽子或增加一条裤子让学生思考更多的搭配方式，通过推理找到增加后的搭配数量与增加前的数之间的关系，渗透递推推理的思想。

“数图形的学问”的递推推理是在增加站点的过程中实现的，缺乏线段增加条数与端点个数的关系总结，教师如果能加强算式的意义解释，可以帮助学生更好地发现与解释规律。

針对“比赛场次”，教材中呈现了更加完善的递推推理，但是学生在解决问题时一般不用这种推理方式，更多的是关注问题本身的答案，运用以往的经验孤立地解决问题。引入递推推理需要更多地发挥教师的主导及提示引领作用。

五、需要进一步研究的问题

在小学阶段，“计数方法”虽有所体现，但学生主要是基于示意图、列表格、连线的解题策略的有序列举积累活动经验，然后运用加法或乘法的意义列式计算，对加法原理和乘法原理以及排列和组合思想方法的体验不深。为此，笔者以为需要进一步加强下列问题的研究：（1）如何基于有序列举，根据“计数原理”和排列组合的基本概念展开更加结构化的教学，使学生更好地积累结构化的活动经验？（2）排列组合的思想方法是否需要在小学阶段渗透？在教学中应该渗透到哪一步？如何渗透？