推算作图法在方格作图中的应用

殷素文

【摘 要】小学阶段的方格作图是指在已有的方格图中，按照长度、面积或平移旋转等要求作出图形。本文源于一次课堂上的教学意外，思考并提炼出推算作图法，可以在原有常规思维方法的基础上，用探索、逆向思维的实践方式，挖掘方格图中隐藏的点和线，解决了一些常规作图无法实现的特殊作图问题，拓展了作图方法。

【关键词】方格作图 推算作图法 隐藏

一、案例引入，“催生”推算作图法

课堂上讨论一题：

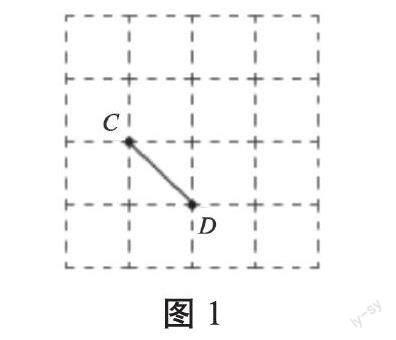
图1中的小方格是边长为1厘米的正方形。以CD为一条边，画出一个三角形CDF，使三角形CDF为等腰三角形，且面积为1平方厘米。则符合条件的点F共有（ ）个。

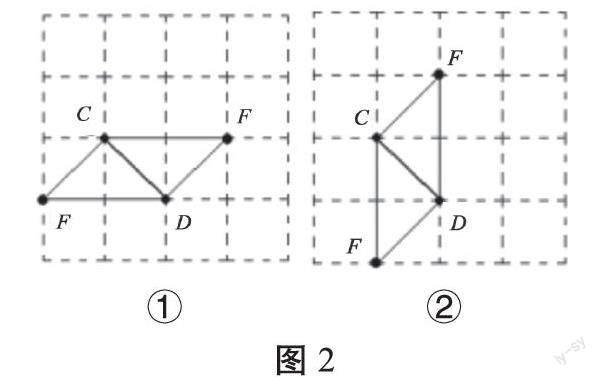
课堂上先独立完成，再小组讨论，最后交流讨论得出4种作图方法：以CD为腰，底在横线上有两种画法（见图2①）；以CD为腰，底在竖线上有两种画法（见图2②）。并用三角形面积公式进行检验。

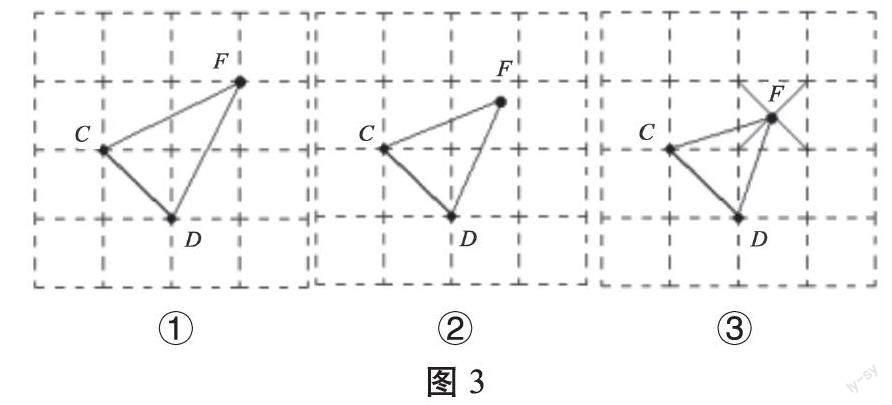
少顷，学生1举手说还有一种方法，教师邀请其上讲台。学生1画出点F并连线（见图3①）并说明：以CD为底，另两条为腰，这样三角形面积也是1平方厘米。

许多学生投来了诧异的目光，教师追问：“是1平方厘米吗？”经讨论得出三角形CDF的面积是1.5平方厘米，显然点F的位置不符合题目要求。（用包含三角形CDF的边长为2厘米的大正方形面积，减去里面的其他3个小三角形面积。这里意外地复习巩固了不规则图形的另一种求面积方法）这时学生2说：“可以的！”便快速跑到讲台上，修改了点F的位置（见图3②）并说明：以CD为底，只要把高变矮些，面积就可以是1平方厘米。很多学生表示认同，教师问：“点F的位置在哪儿呢？随手一画肯定不行。”教室里出现了支支吾吾的声音，但又没有人举手，讨论仿佛又回到了原点：答案只有4种！？“老师，我能找出点F。”学生3随即冲上讲台，再次修改点F的位置（见图3③）并说明：点F是1小格的中心，三角形CDF的高是图3①中高的2/3，面积也就是1平方厘米。其他学生向学生3投来惊奇的目光，教室里安静了下来，教师表扬3个学生，并给予奖励。显然，图3③的三角形CDF的底和高同为厘米，虽然此三角形面积在小学阶段无法计算，但沿着上述思路，可以很容易推算出三角形CDF的面积。这样点F的位置比原先又多了2种（另一点在以CD为对称轴，已知点F的对称位置，即CD的左下方）。这里把后两种寻找点F位置的方法且称为“推算作图法”。

二、灵活运用，“演绎”另一种精彩

上面例子中用推算作图法找点F位置与前4种有着明显的不同。前4种是紧扣三角形的面积公式，脑海中思考的是：（底）×（高）÷2=1（平方厘米），要用合适的底和高进行计算，底和高的大小被限定在整数范围之内；推算作图法先假设CD是三角形的底，以点F的合理位置为思维起点，思维更加倾向于有效推理，三角形CDF底和高不计入，在寻找点F的过程中先出错，再融错。可见，推算作图法包含的先假设，再融错的理念与解决“鸡兔同笼”的问题时用的方法（可以先假设全是鸡，发现腿的数量变少了，查找原因是“兔子惹的祸”，兔子的数量“暴露”了，鸡的数量也就出来了）有异曲同工之妙。推算作图法有其特有的优点，在实际操作中可充分加以利用。下面举几个例子说明推算作图的“拿手绝活”。

例1：在方格图中画出面积分别为2平方厘米、5平方厘米的正方形。（小方格是边长为1厘米的正方形，下同）

如图4①，左下角实线表示的正方形面积是2平方厘米，向右上方拓展，可以得到面积为4平方厘米、6平方厘米的新长方形。

如图4②，正方形的面积为5平方厘米（思考及作图方法可参考后文举例），同样也可以画出面积为8平方厘米、10平方厘米的正方形。

例2：在方格图中画出面积为7平方厘米的平行四边形（高和底都大于1厘米）。

由于高和底的條件限制，使得乘法口诀里得数是7 的口诀派不上用场了。但通过推算作图法的思维，可以尝试寻找6.□×1.□=7的可能性，或者是2.□×3.□=7的可能性。通过尝试与推算，就可以得出图5中的两种面积同为7平方厘米的平行四边形。从上面的例子可以看出，推算作图法不局限于整数类型的计算作图，从可能性的角度出发，尝试并推算猜测的作图方法是否存在，思维更灵活，更具挑战性，得出的结果也更加“出人意料”。

三、有容乃大，“升级”方格图的认识

对图3，大家也许会觉得似乎哪里不太对劲，下面笔者就来谈一谈对方格图的进一步认识。

如图6①，图中的点和线其实只是对已有方格的部分描摹，使之更加清晰，这些直观存在的点和线，也是我们平时直接利用的。

图6②中的线段是将方格中任意两点连接产生的，这种隐藏的线，虽然它们的长度不是整厘米数，但是结合直角三角形斜边与直角边的大小关系，学生很容易判断出它们的大小范围，这将有助于学生选取合适的长度用于下一步猜想。比如要画一个面积为5平方厘米的正方形，它的边长应取2厘米到3厘米之间，这样的边在哪儿呢？在一步步地引导、推算中，学生体会到成功的快乐。用这种隐藏的“暗线”解决问题，有时含金量更高，说明“暗线”也可加以利用。

图6③是通过简单的连线产生的“暗点”，这种“暗点”精确地表示某一固定位置，也是方格图自身特点所赋予的特征。如果学生用简单、快捷的方法找出这些隐藏的点（保留作图痕迹），并且这些点在运用中具有准确的数学含义，能解决实际的问题，就说明它有利用价值，也有其存在的理由。这样看来方格图只是我们作图的一个参照系，在这个参照系中快速建立起来的“暗线”和“暗点”同样也是这个参照系的一部分，可以作为参照物来使用，等待我们去发掘、利用。悦纳这样的“暗线”与“暗点”将使作图的世界更加精彩。

四、包容会通，不“拘泥”效率第一

过去，我们的课堂教学都紧紧围绕着课前设定的教学目标来开展，把能否完成教学目标作为一节课是否成功的重要标志。而这一预设的教学目标又大多以教师对教育教学的认知为基础，把既定的线性课堂教学过程作为参考路线，对学生“节外生枝”的想法包容度不够，课堂教学变成了教师“引”、学生“跟”，学生很难跳出教师预设的思维框框。课堂上的意外在一定程度上还原了学生在学习过程中的真实想法，它脱离了教学的预设目标，但它体现了学生对学习中可能性的另一种探索。教师不能因为课堂时间的限制等因素，把教学时效放在首位，而忽视了学生学习过程中探索精神的培养。正是由于课堂上学生敢闯、敢试、敢辩，才打开了方格作图的另一扇窗，发掘出了方格图中的隐藏条件，用推算的方法实现了作图“自由”。推算作图法扩展了方格作图的外延，引领我们进入了一个“不规则”的世界。或许推算作图法的“能效比”并不占优势，但它拓宽了学生的视野，培养了学生敢于估测、尝试的精神，学生思维的质量高，过程曲径通幽，结果回味无穷。也许推算作图法与一般计算作图法的结合才是方格作图的完美呈现。