一种用于医疗EEG数据集的联邦遗传算法

陈海宇

（肇庆医学高等专科学校公共卫生学院，广东肇庆 526070）

0 引言

随着数字化在社会和经济等各个方面的不断普及，导致产生的数据量不断增加.在处理用户生成的敏感数据时，如何保护用户的隐私不被泄露是一个重要问题，也就是说，用户不希望其他人对其拥有的机密信息进行分析，从而得出任何结论［1］.联邦学习的提出，加强了用户的隐私保护，为解决此问题提供了一种有效方法［2］.

医疗领域是联邦学习的一个重要应用领域［3］.每个医疗机构可能拥有大量的患者数据，但是基于这些独立数据，不足以构建并训练出性能良好的预测模型，进而更好地服务于医疗工作.针对这个问题，医疗机构之间共享数据，可以极大地帮助开发自动化诊断工具，从而有效解决这个问题.但是这些患者数据都属于私人信息，医院有义务保护患者的隐私，再加上法律法规的约束，阻碍了机构之间的数据共享［4］.联邦学习的应用可以帮助医疗行业的不同机构，在不共享患者数据的情况下，联合训练机器学习模型［5，6］.

为了解决全局模型的学习问题，联邦学习的主流方式如下［7，8］：首先，根据问题的先验知识，构建一个基础的神经网络结构，用户利用某种梯度下降的方法训练局部模型；然后，服务器端聚合各局部模型参数，完成全局模型的更新.这个过程经过多次迭代，最终实现神经网络的训练.联邦平均算法是一种典型的联邦学习算法，在解决聚合问题时具有很好的效果，但这种方式仍然面临着一些威胁［9，10］.例如，当攻击者获得了全局模型，并劫持了用户的局部模型更新梯度时，就可以倒推出用户的部分隐私数据.为了进一步加强用户的隐私保护，差分隐私、安全多方计算等方法被应用到联邦学习算法中［11］.虽然这些方法很有效，却给联邦学习带来了更大的计算压力和通信开销.

最近，研究人员提出了一种新颖的方法［12］，其主要思想如下：结合遗传算法的相关知识，在不使用梯度的情况下训练全局模型，该算法将从单个用户到服务器的数据传输减少到单个适应度值.通过这种方式，用户不需要上传模型的梯度信息，进而提高了数据的安全性.在该算法的实验中，使用卷积神经网络对脑电波EEG（electroencephalography）信号进行分类，验证了遗传算法应用于联邦学习的可行性.本文基于该算法，使用改进的遗传算法对模型进行优化，并与该算法进行了比较.

1 具体模型

1.1 神经网络模型结构

全局模型的结构对于联邦学习的实际表现至关重要.针对上述问题，选择专门为脑电图预测问题设计的文献［13-15］中介绍的浅卷积网络.该网络的核心是3个卷积层，旨在识别信号中的特征信息.前两个卷积层之后是一个池化层，随后是第三个卷积层.在这一层的输出上，应用批处理归一化，然后添加了带有sigmoid激活函数的全连接输出层.

1.2 目标函数

为了使适应度在遗传训练中最大化，选择负均方误差（NMSE），计算方法如式（1）所示：

结合NMSE进行适应度的评价，原始的单目标优化问题就转换为优化神经网络中w的值，使得计算出的NMSE值最大化，如下式所示：

在本文中，个体的生成，即选择、交叉和变异发生在中央服务器的一个集中位置.系统的连接节点通过评估不同的设置来参与优化.一个个体的适应度可以通过对局部适应度值的加权平均来计算.

2 基于改进遗传算法的问题求解过程

在本节中，将描述求解问题时不同阶段采用的特定方法.

（1）编码

使用直接编码方式对上述介绍的神经网络进行编码，模型中的连接权重等参数使用实数进行编码.例如，对于具有30个卷积核的卷积层，卷积核的大小为1×25时，对应的编码采用30×1×25的矩阵进行实数编码.

（2）种群初始化

开始时，创建一个初始种群，其中每个个体随机初始化模型的权重.从初始种群开始，沿着计算适应度-选择-交叉-突变循环迭代.

（3）交叉操作

交叉方式决定了从父代生成新个体的方法，从种群中随机选择两个父代个体，用于生成子代.下面介绍了4种交叉的方式：

（a）对半混合：这种交叉方式实现起来比较简单，通过将第一个父代个体的基因前半部分与第二个父代个体的基因后半部分结合在一起，构成子代的基因型，使用式（3）表示：

其中，n为个体基因向量的长度，并且a=(a1,a2,…,an)，b=(b1,b2,…,bn)代表了两个父代的基因向量，1 ≤i≤n.

（b）交错混合：在这种方式中，来自两个父代的基因向量通过交错赋值的方式，来创建后代向量，如下式所示：

其中，n为个体基因向量的长度，a和b代表两个父代基因向量.

（c）均值混合：在这种交叉方式中，取两个父代个体的基因向量在相同位置上的平均值，创建子代的基因向量，可以表示为下式：

其中，n为个体基因向量的长度，a和b代表两个父代基因向量.

（d）卷积核交叉：这种交叉的方式，较上述3种有着本质上的不同，特点是保留了部分父代个体的模型信息.在每个卷积层中，有多个卷积核/过滤器.这些卷积核对数据进行特征提取，保存着关键的模式信息，从而帮助神经网络更好地学习数据集.类似地，在全连接层中，神经元的输入权重也描述了前一层的某些模式.卷积核交叉通过将父代基因向量中每一层的卷积核随机混合，生成子代个体的基因型.这种方式保证了交叉过程中卷积核的完整性，使得神经网络的模式信息得到保留，表达式如式（6）所示：

其中，num_channel为个体基因向量中卷积核的个数，a和b代表两个父代基因向量，channel_i表示第i个卷积核，μ为取值范围在0-1之间的随机数.

前3种交叉方式，实现过程比较简单.由于没有考虑到神经网络的结构和卷积核的学习模式，在一些实验中模型的收敛性能较差.卷积核交叉方式是一种更高层次的方法，用来作为遗传神经网络的交叉方式，具有很高的适用性.在自然界中，遗传也是一种更高层次的基因混合，而不是有机分子的低层次混合.因此，父母的特征是完整的，它与遗传学的相似之处可以概括为：DNA 代表了网络的权值，而基因则代表的是卷积核.本算法采用了卷积核交叉来进行交叉操作.

（4）变异

交叉操作本质上是父代个体的交叉组合，在此基础上，使用变异操作增加产生新个体的潜力，可以进一步扩大算法的搜索空间，找到适应度更高的个体.为了定义变异算子，首先需要定义变异基因的数量和这些基因上的改变量.对于前者，使用一个概率值来确定个体基因中每个值的变异概率；后者是一个浮点值，用于确定对每个变异基因的变化量.下面介绍两种执行变异操作的方法：

（a）通过偏移量变异：这种方式，通过对产生变异的节点添加一个随机值，完成变异的操作.在具体的实现中，使用到的偏移量是取值范围在[-mutation_rate,mutation_rate]之间的一个随机值，mutation_rate表示变异概率.

（b）通过乘法进行变异：在这种变异方式中，对产生变异的节点与一个随机值相乘.在具体的实现中，乘法因子取值范围是在之间的一个随机值.

在本文的实验中，选择第二种变异算法.

（5）选择

通过对当前种群基于适应度函数值进行排序，得到候选种群.选择种群中适应度函数值最高的n-1个个体，并在种群中余下的个体间随机选择一个，共同组成下一代种群.这样做的原因是可以增加种群的多样性，改善遗传的方向.

（6）精英保留策略

为了防止种群个体在遗传过程中发生遗传衰退的现象，在本算法中，加入了覆盖法［6］作为种群更新的策略.覆盖法的算法流程如下：

Step 1：计算当前子代个体的适应度，根据适应度值降序排列当前子代种群中的个体.

Step 2：根据一定的覆盖比率，将当前子代种群中的前ReN个体替换为精英个体.

其中ReN的大小可以根据种群规模的大小进行自适应的变化.计算公式如下式：

其中，ReN是当前子代种群中的个体，Rreplace是种群覆盖比率，sizepop为当前子代的种群规模.精英保留策略是精英遗传算法的特有策略，可以有效地防止遗传倒退现象的发生，同时加快搜索效率.

3 仿真实验

在本节中，仿真实验所用电脑配置如下：64 位Windows 操作系统，处理器为八核Intel Core i5-9300H CPU@2.40 GHz，内存为24 GB，并使用python进行了仿真实验.

3.1 数据集

在实验中，使用了脑电波（EEG）数据集［13］.该EEG数据集对122个受试者分别进行了120个刺激实验.受试者包括两类：酗酒者与正常对照组.在每个实验中，向受试者展示一张或两张Snodgrass和Vanderwart图片集中的图像，接收到刺激后，对他们的脑电波进行采样，然后根据受试者所属的类别对脑电波图像进行标签的标记.因此，所建立的模型的任务是，根据受试者的脑电图，预测受试者属于两类人群的哪一类.

3.2 实验参数设置

本实验中使用的神经网络结构使用如下设置［14］：输入的数据维度为（64，256，1），输出的类别为两类：酗酒者与对照组.采用的神经网络具有3个卷积层，第一个卷积层具有30个卷积核；后面的两个卷积层分别具有10个和2个卷积核，并且在第二个卷积层与第三个卷积层之间加入了一个平均池化层；最后是一个全连接层，采用softmax函数进行分类.

遗传算法中的种群大小设置为50，考虑到本算法中没有使用梯度进行模型更新，使得模型收敛的速度较慢，迭代次数设为3 000，保证模型最后能够收敛到一个稳定的水平.交叉采用了卷积核交叉算法，变异操作中的变异概率设为0.01.

过拟合是深度学习中经常出现的问题，避免过拟合的主要思想是，在模型的训练期间，不要把整个数据集一次性分配给模型学习.在每一次迭代中使用训练数据的子集进行训练，训练集的子集可以每次迭代更改一次，也可以保持几次迭代不变.通过这种方法，可以有效地避免模型训练后产生过拟合问题.

本实验中为了避免过拟合，在遗传联邦学习的每一代中，随机选择数据集整体的一个子集，对当前种群的适应度进行评估.

3.3 实验结果与分析

在服务器上，保留一个验证集，在每一代中，计算并存储当前一代中最适合的模型精度，使用本文带有精英保留策略的遗传算法对该问题进行优化.同时，为了对比本文算法的效果，在相同的参数设置下，使用遗传算法对该问题进行优化.结果如图1和表1所示.

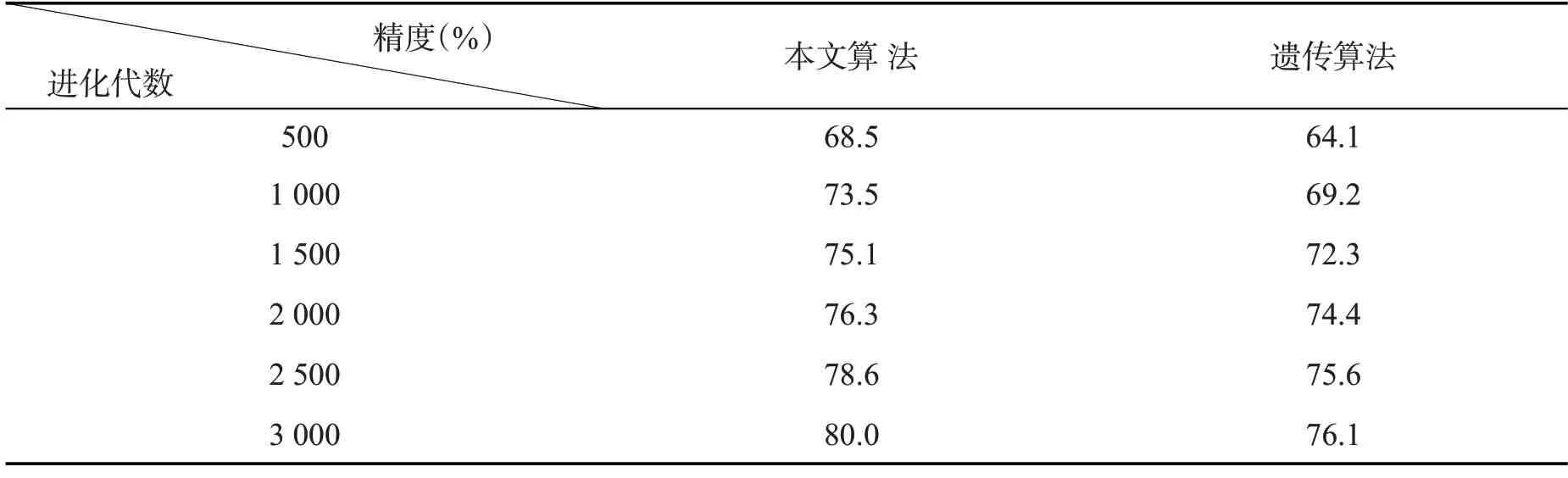
表1 相关算法模型精度对比

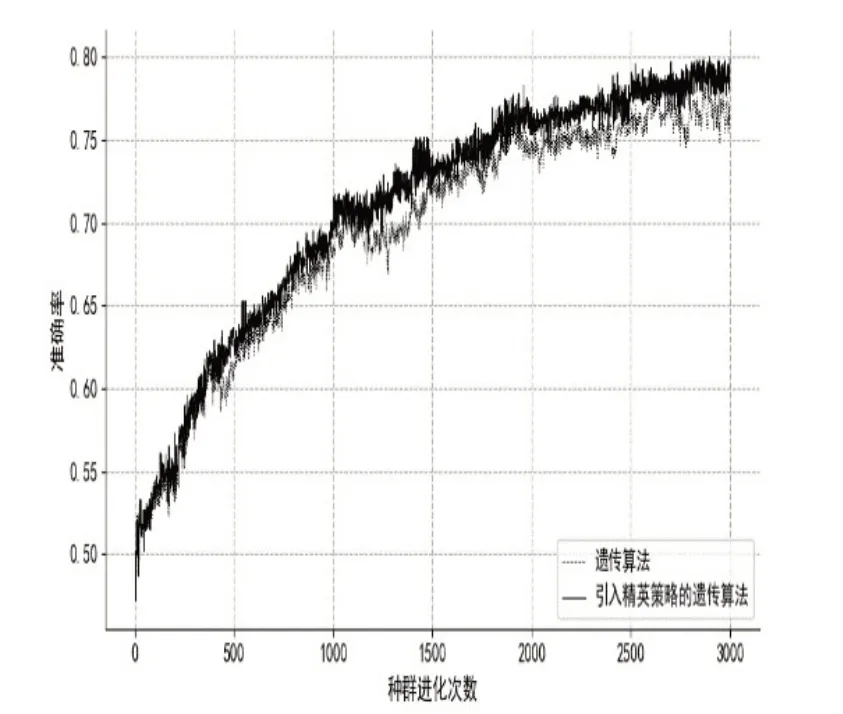
图1 模型精度

使用两种优化算法，得到的种群的适应度函数值变化曲线如图2和表2所示.

表2 相关算法模型适应度对比

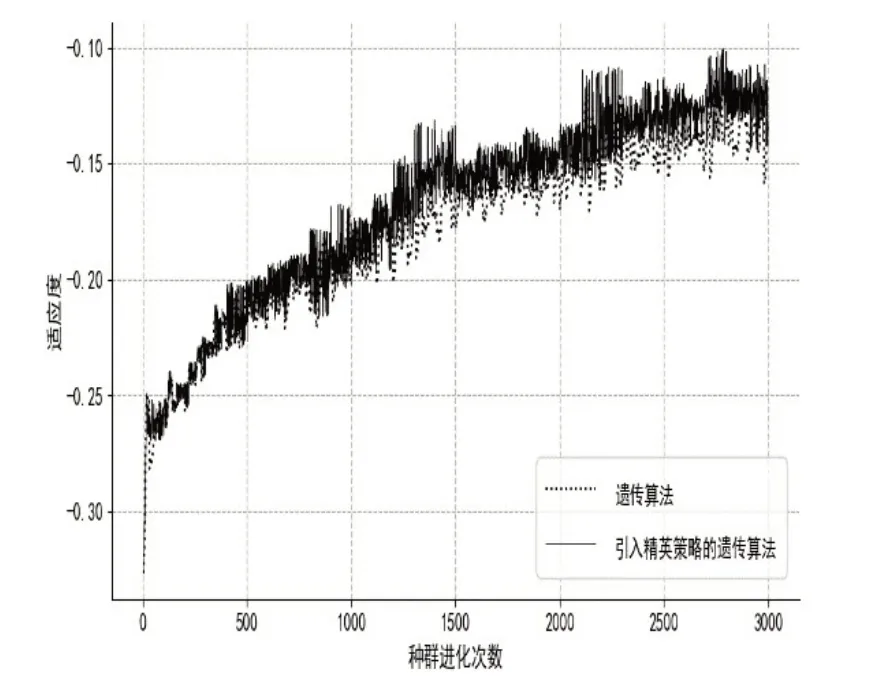
图2 模型适应度

根据图（1）和图（2）可以观察到本算法收敛是缓慢但稳定的.相较于遗传算法，本文提出的算法具有更好的搜索性能.从一个完全随机的状态下，该算法能够达到80%的模型训练精度.虽然这低于深度神经网络学习的平均水平，但考虑到模型的更新过程中没有使用梯度，而是使用了遗传算法的适应度值作为代替，这仍然是一个很好的结果.

4 结论

联邦学习结合遗传算法的一个优势是，客户端传输到服务器的数据更少.虽然本文算法收敛速度要慢一些，但由于只公开了模型的一个适应度函数值，而无需传输模型的梯度信息，从而提高了数据的安全保障能力.本文算法实际上是通过牺牲一定的学习速度来保护数据的隐私，因此，对于一些特殊应用场景有着较大的优势.比如：对于来自医疗机构的数据，学习过程的通信开销并不是最重要的，而保持用户数据的隐私才是至关重要的.实验结果表明，本文算法较好地保障了医疗数据的隐私安全，具有一定的应用价值.