菲涅尔衍射积分的角谱算法

韩佳成,郭文雅,赵亚楠,杨丽君,王颖,张素恒

(河北大学 物理科学与技术学院,河北 保定 071002)

菲涅尔衍射积分公式是标量衍射公式的近似,可以计算傍轴区域的衍射光场分布[1-3],广泛应用于数字全息[4-6]、光学图像加密[7-9]、光束整形[10-13]等领域.而在一般情况下,菲涅尔衍射积分并不存在解析解,需要借助于数值算法求解[14-15].角谱算法是一种常用的数值计算方法,它基于菲涅尔衍射的线性空间平移不变性,利用离散傅里叶变换将物光场分布与系统脉冲响应函数的卷积运算转换为物光角谱与系统传递函数的乘积运算,大大降低了计算的复杂度.得益于线性系统理论和快速离散傅里叶变换,角谱算法概念清晰,应用方便,并且具有较高的计算效率,因而受到广泛关注.

尽管已有文献分别对数值计算菲涅尔衍射积分时二次相因子的采样间隔[16-19]、物光矩阵的零填充[20-22]以及窗口尺寸计算[23-26]等因素进行了大量的讨论.然而在角谱算法的具体实施过程中,这些因素相互依赖、彼此关联,它们共同决定了数值计算的正确性与计算精度,因此,需要从整体的角度统一梳理这些因素的相互关系,澄清有关问题,以确保角谱算法的正确实施.

本文首先从空间滤波的角度详细阐明了角谱算法的具体实施过程,澄清了理想采样条件的来源,指出理想采样条件是角谱算法获得正确结果的前提条件.按照理想采样条件,采样间隔反比于计算窗口尺寸,对采样间隔的限制会影响到计算窗口尺寸的选择.清晰解释了离散傅里叶变换的循环卷积会引入卷绕误差,指出选取较大的计算窗口尺寸相当于进行零填充可以有效避免卷绕误差,还明确给出了循环卷积与线性卷积相等的区域.详细列出了影响计算窗口尺寸选取的因素,给出了计算窗口尺寸的选取依据.这些方法和依据将有效地避免角谱算法应用过程中所遇到的问题,从而保证计算的正确性与计算精度.然后,采用角谱算法数值计算了高斯光束照明余弦光栅的菲涅尔衍射场.数值解与解析解的对比表明,当满足理想采样条件并正确选取计算窗口尺寸时,角谱算法可以达到非常高的计算精度.最后还采用角谱算法仿真了单透镜相干成像实验,进一步展示了角谱算法的应用过程.

1 菲涅尔衍射的角谱算法

1.1 菲涅尔衍射角谱公式

在无限大不透明衍射屏上开有一长、宽分别为Wx、Wy的矩形衍射窗,物体分布于衍射窗内,以衍射窗中心为原点建立坐标系,如图1所示.当单色相干光场照明衍射屏时,其后距离为z的观察屏上的光场分布由菲涅尔衍射积分公式给出[25],见式(1).

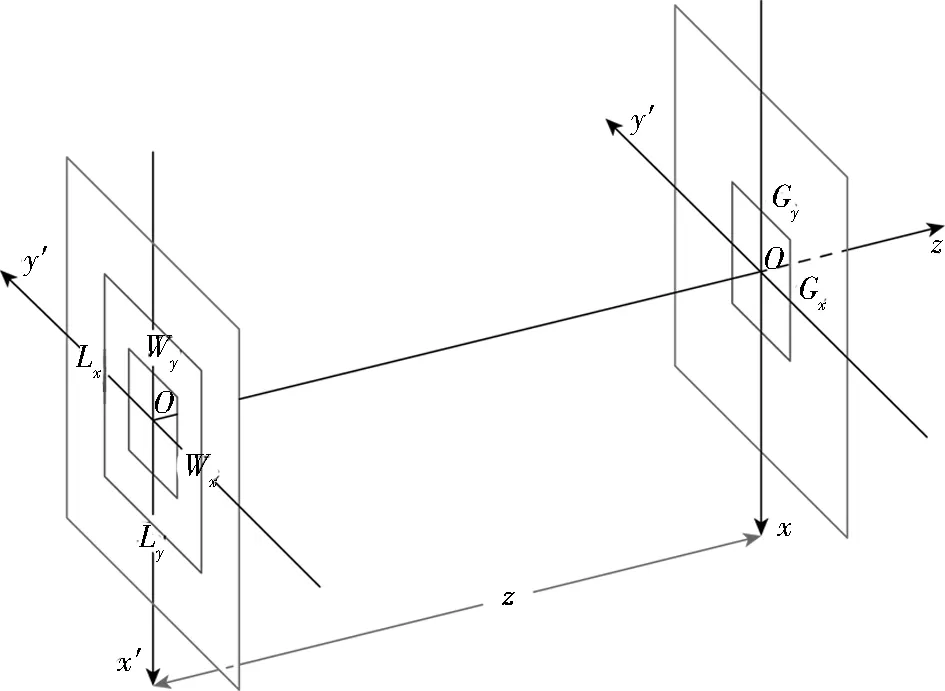
图1 菲涅尔衍射坐标系示意Fig.1 Coordinate system of the Fresnel diffraction

(1)

其中,U0(x′,y′)和U(x,y)分别为衍射屏后表面物光场复振幅与观察屏上衍射光场复振幅,λ为波长,k为波数,对整个衍射屏后表面进行积分.exp(jkz)为光场纵向传播引起的相位延迟,它在整个观察屏上均匀分布,下文略去该相位因子.

若将菲涅尔衍射看成一个光学系统,衍射屏后表面作为系统的输入面,观察屏作为系统的输出面,并且该系统的输入输出关系由式(1)给出的卷积积分描述,于是菲涅尔衍射可看成一个线性空间平移不变系统,其脉冲响应函数为

(2)

这时菲涅尔衍射公式可表示为卷积形式,即

U(x,y)=U0(x,y)*h(x,y),

(3)

其中,*为卷积运算符.若从空间滤波的角度来理解菲涅尔衍射,衍射屏后表面的物光场经滤波器滤波后即得到观察屏上的衍射光场.

对于空间滤波系统,还可以在频谱域中讨论输入输出关系.在标量衍射理论中,光场分布的空间频谱又称为角谱.于是衍射屏后表面上物光场的角谱A0(ξ,η)与观察屏上衍射光场的角谱A(ξ,η)分别为

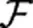
(4)

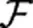
A(ξ,η)=A0(ξ,η)H(ξ,η),

(5)

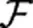
H(ξ,η)=exp[-jπλz(ξ2+η2)].

(6)

利用式(5)得到观察屏上光场的角谱A(ξ,η)后,再进行傅里叶逆变换即可计算出观察屏上的衍射场分布

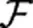
(7)

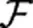
1.2 菲涅尔衍射角谱公式的离散化

在数值计算菲涅尔衍射场时,需要对式(7)进行离散化.首先在衍射屏后表面以原点为中心选取一长、宽分别为Lx、Ly的计算窗口,使其包含衍射窗,如图1所示.然后再以采样间隔δx、δy沿x′、y′对计算窗口内的物光场进行采样,得到计算窗口内物光的采样矩阵

(8)

其中,各采样点的坐标分别为

(9)

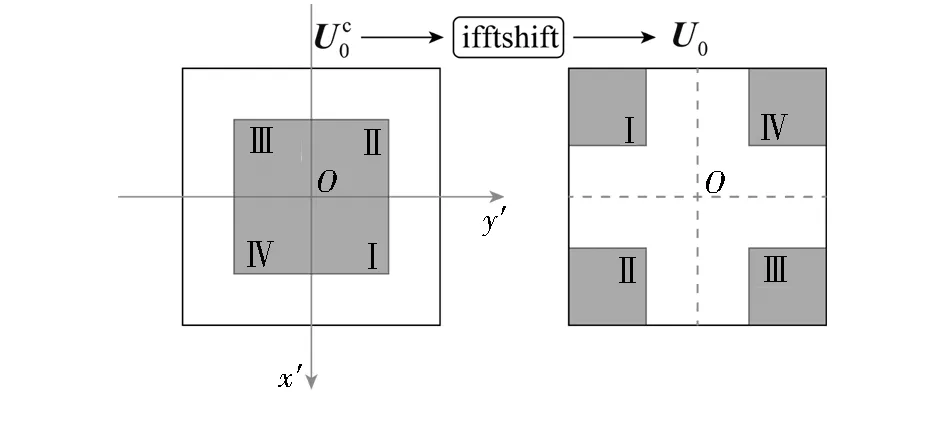
图2 利用ifftshift操作将坐标原点从矩阵中心移至左上角Fig.2 Shifting the origin from the center of the matrix to the top left corner through the ifftshift operation

(10)

其中,坐标取值分别为

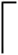
(11)

对物光矩阵U0进行离散傅里叶变换得到物光角谱矩阵

A0=FFT2{U0},

(12)

其中,FFT2{·}代表二维快速离散傅里叶变换.物光角谱矩阵各取样点的坐标

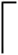
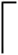
(13)

由离散傅里叶变换的性质可知,对于采样间隔为δ、长度为M的离散序列,其离散频谱序列的采样间隔为1/Mδ.因此,物光频谱矩阵A0在谱频空间沿ξ与η方向的采样间隔分别为

(14)

按照物光角谱矩阵所决定的采样间隔(式(14))与采样点坐标(式(13))对衍射系统传递函数H(ξ,η)进行采样,得到传递函数的采样矩阵

(15)

然后将物光角谱矩阵A0与传递函数矩阵H代入式(7),可计算出观察平面上的衍射场分布矩阵

Uw=IFFT2{A0∘H},

(16)

其中,IFFT2{·}代表二维快速离散傅里叶逆变换,∘代表Hadamard乘积.但直接逆变换得到的衍射场分布矩阵Uw的坐标原点位于矩阵左上角,需要通过fftshift操作,将坐标原点移至矩阵的中心,即

(17)

调整后的坐标分别为

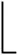
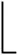
(18)

这种数值计算菲涅尔衍射积分的方法称为角谱算法.

1.3 理想采样条件

利用角谱算法数值计算菲涅尔衍射积分时,间接涉及对传递函数进行采样.从式(6)可以看出,传递函数由单位振幅的二次相因子构成,不是带限函数.在整个频谱平面上,采样总无法满足采样定理的要求.但在数值计算时,仅对有限频率范围内的传递函数进行采样.由式(13)、(14)可知,沿ξ与η两个方向对传递函数采样的频率范围分别为

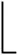
(19)

其中,M=Lx/δx,N=Ly/δy.2009年VOELZ等[18]采用局域空间频率的概念证明只有当空域采样间隔满足

δx=λz/Lx,δy=λz/Ly,

(20)

传递函数H(ξ,η)的采样矩阵H(u,v)才与计算窗口内脉冲响应函数h(x,y)的采样矩阵h(m,n)互为离散傅里叶变换对,并称式(20)为理想采样条件.值得一提的是,在理想采样条件下,角谱算法与脉冲响应函数法[18]完全等价.

理想采样条件是确保角谱算法获得正确结果的前提条件,下述讨论均以理想采样条件为基础.考虑到理想采样条件,传递函数的采样矩阵可表示为

H(u,v)=exp[-jπ(u2/M+v2/N)],

(21)

其中,各取样点的坐标分别为

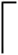
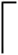
(22)

1.4 循环卷积与卷绕误差

利用角谱算法数值计算菲涅尔衍射积分时,会受到离散傅里叶变换带来的循环卷积的影响.按照离散傅里叶变换的循环卷积定理,式(16)可以表示为

Uw=U0○*h,

(23)

其中,○*代表循环卷积.h=IFFT2{H}为计算窗口内脉冲响应函数的采样矩阵,其中各采样点坐标取值由式(11)给出.由式(23)可知,计算得到的衍射光场分布矩阵Uw为计算窗口内的物光采样矩阵U0与脉冲响应函数采样矩阵h的循环卷积.然而,实际观察屏上衍射光场分布U应为U0与h的线性卷积,即

U=U0*h.

(24)

循环卷积与线性卷积的差常称为卷绕误差.

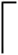
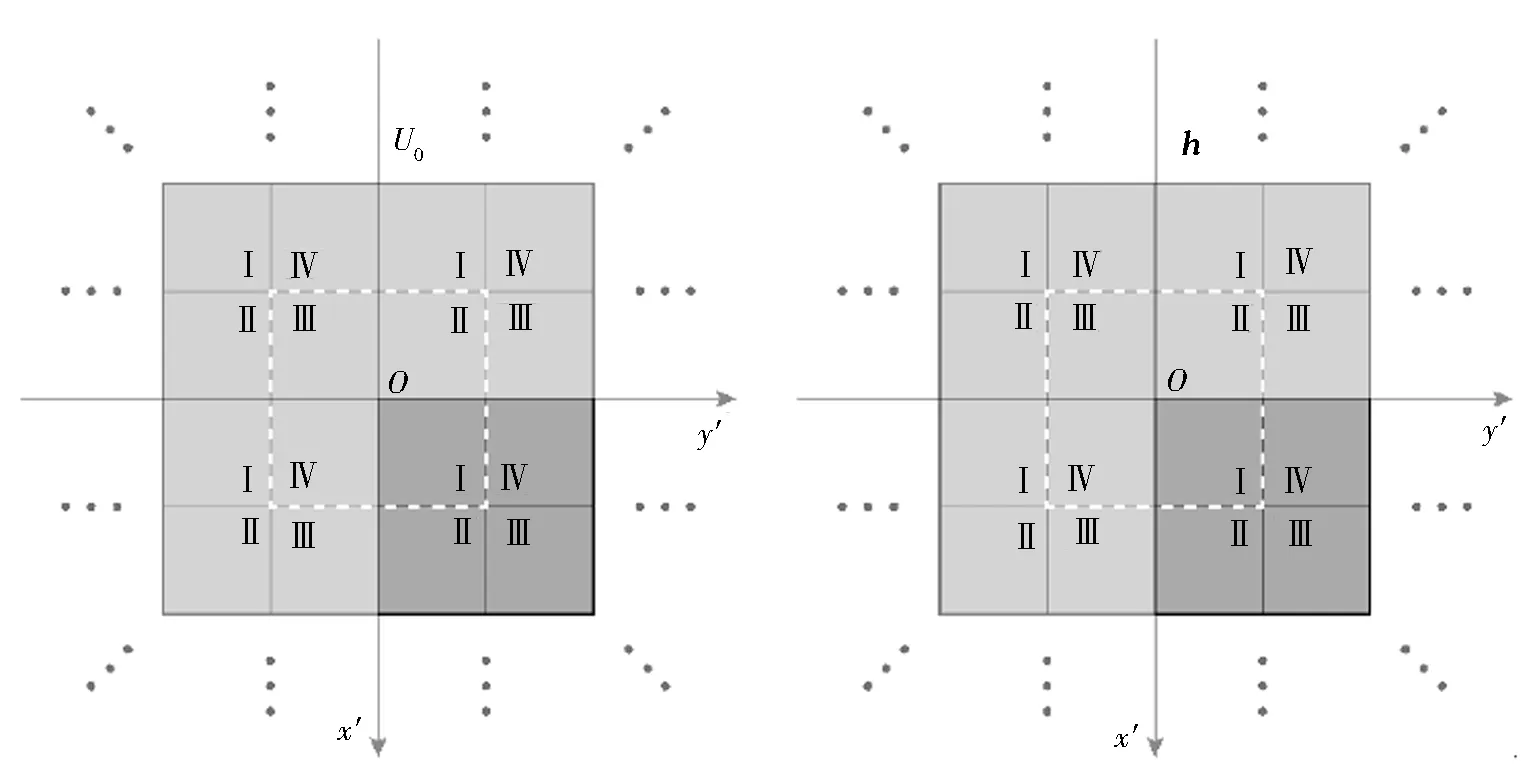
图3 计算窗与衍射窗尺寸相同时周期延拓后的U0和hFig.3 Period extended U0and h when the sizes of the calculation window and diffraction window are the same

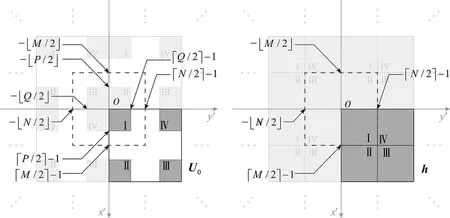
图4 计算窗大于衍射窗尺寸时周期延拓后的U0和hFig.4 Period extended U0and h when the calculation window size is larger than the diffraction window size

(25)

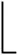
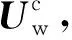
(26)

1.5 计算窗口尺寸的选择

在利用角谱算法计算菲涅尔衍射时,有多种因素影响计算窗口尺寸的选取.计算窗口尺寸的选取主要考虑到以下因素:

1)计算窗口尺寸应满足理想采样条件(式(20)),在衍射距离确定的情况下,计算窗口尺寸与采样间隔并不独立.对采样间隔的限制会影响到计算窗口尺寸的选取.对衍射窗内物光场采样应满足采样定理,即采样间隔应满足

1/δx≥Bx, 1/δy≥By,

(27)

其中,Bx、By分别为物光场沿x′、y′的带宽.考虑到理想采样条件,要求计算窗口尺寸满足

Lx≥λzBx,Ly≥λzBy.

(28)

2)若观察窗的尺寸为Gx、Gy,以z轴与观察面的交点为中心,如图1所示.经采样后,观察窗内采样点坐标集合为

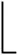
(29)

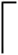
Lx≥Wx+Gx,Ly≥Wy+Gy.

(30)

若要得到完整的衍射场,需要观察窗的尺寸最小[22],

Gx=Wx+λzBx,Gy=Wy+λzBy.

(31)

这时计算窗口的尺寸应满足

Lx≥2Wx+λzBx,Ly≥2Wy+λzBy.

(32)

3)计算窗口的尺寸越大,采样点越多.在理想采样条件下,计算窗口内沿x′、y′的采样点数分别为

(33)

为了减小计算量,Lx和Ly应取在式(30)的下限附近,并使式(33)得到的M、N恰好为整数,这也方便计算.

2 数值仿真实验

2.1 高斯光束照明余弦光栅的菲涅尔衍射

高斯光束照明无限大二维余弦光栅时的菲涅尔衍射积分具有解析解.这时可以将数值计算结果与采样后的解析解进行比较,来检验数值算法的计算精度.

在图1中的衍射窗内放置一个二维余弦光栅,沿z轴正向传播的基模高斯光束从衍射屏左侧垂直入射到该余弦光栅上,且高斯光束的束腰正好位于光栅所在平面,则衍射屏后表面上的光场分布可表示为

f0(x′,y′)=e-π(x′2+y′2)/α2cos(2πξ0x′)cos(2πη0y′),

(34)

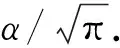
f(x,y)=[fξ0(x)+f-ξ0(x)][fη0(y)+f-η0(y)]/4,

(35)

其中,fξ(x)的具体形式为

fξ(x)=Kξexp[-π(x-λzξ)2/σ2]exp[j2π(κqx2+κlξx)],

(36)

其中,

由于照明基模高斯光束的能量几乎全部位于-2α≤x′≤2α,-2α≤y′≤2α,因此可以认为衍射窗尺寸为Wx=Wy=W=4α时,观察屏上的衍射场分布基本不变,仍可由式(35)来描述.

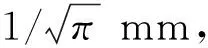
(37)

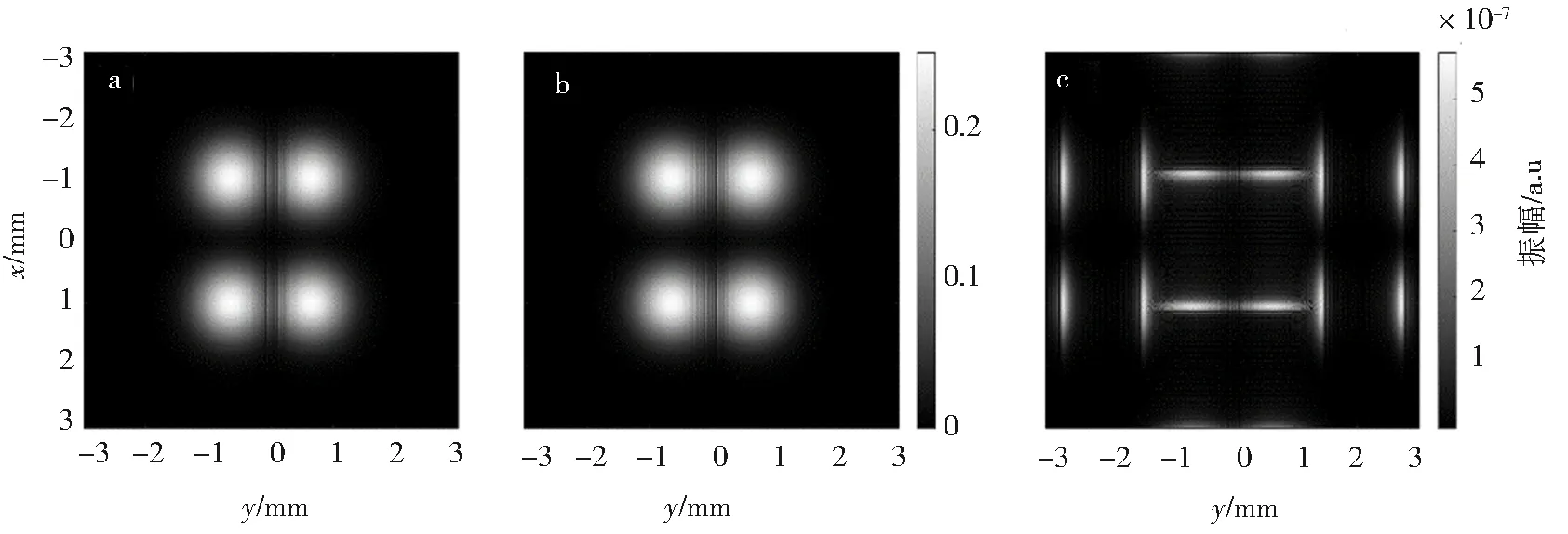
a.数值解U的振幅分布;b.解析解f的振幅分布;c.数值解与解析解差值E的模值分布图5 高斯光束照明余弦光栅的菲涅尔衍射图样Fig.5 Fresnel diffraction pattern of Gaussian beam illuminating cosine grating

为了定量描述数值计算误差,选用均方信噪比RSN作为评价标准,其定义为

RSN=10 lg(∑mn|f(m,n)|2/∑mn|E(m,n)|2),

(38)

其中求和对于矩阵中所有元素进行.根据该定义,数值计算结果U相对于解析解f的均方信噪比为RSN=116.7 dB.当采用理想采样间隔和适当的计算窗口时,角谱算法的性能十分优异.该仿真实验展示了解析物体经历单次菲涅尔衍射的计算过程.

2.2 单透镜相干成像

通常采用菲涅尔衍射分析成像过程.下面采用角谱算法数值仿真理想薄透镜的相干成像过程.如图6所示,理想薄透镜的焦距F=40 mm,其光瞳为边长d=5 mm的正方形,物面与像面分别位于透镜前后2倍焦距处.在物面上,物体放置于物面上边长W=4 mm的正方形衍射窗内,衍射窗的中心与光轴重合.波长为λ=500 nm的单色平面波正入射照明物体,透过物体的光波先后经过2次菲涅尔衍射后到达像面.

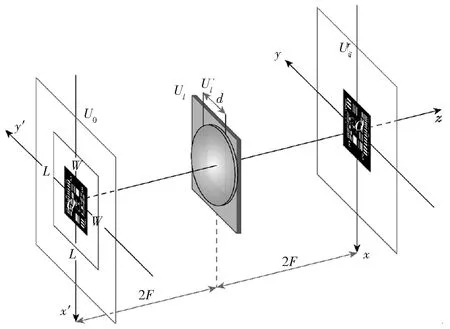
图6 单透镜相干成像示意Fig.6 Schematic diagram of single-lens coherent imaging

仿真物体为USAF-1951分辨率测试板(局部)以δ=4 μm的采样间隔采样后得到的P×Q=1 000×1 000像素的图像,如图7a所示.按照理想采样条件,当采样间隔δ=4 μm时,计算窗口需要取边长L=2λF/δ=10 mm的正方形,其中采样点数为M×N=2 500×2 500.因此,首先需要将图7a所示图像四周零填充至2 500×2 500像素,作为物光采样矩阵U0.利用角谱算法可以计算出透镜前表面光场采样矩阵Ul.由于计算窗的边长L=10 mm,衍射窗的边长W=4 mm,在计算出的透镜前表面的衍射场分布矩阵Ul中未受卷绕影响的区域为L-W=6 mm的正方形.而透镜的光瞳为边长d=5 mm的正方形,因此,在透镜光瞳内是正确的衍射场.

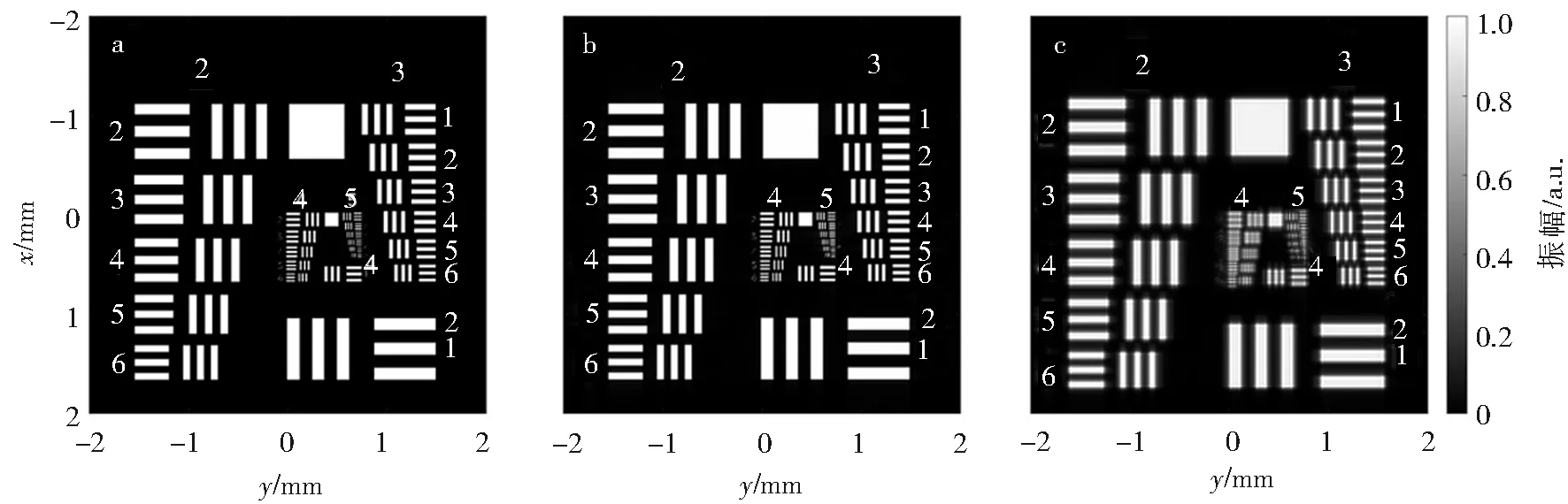
a.离散物体图像;b.等大成像仿真结果的振幅分布;c.轻微离焦成像仿真结果的振幅分布图7 单透镜相干成像中离散物体图像与数值仿真结果Fig.7 Discrete object image and numerical simulation results in single-lens coherent imaging

透镜的复振幅透过率为

T(x,y)=exp(-jk(x2+y2)/2F)rect(x/d)rect(y/d),

(39)

其中,rect代表矩形函数.对透镜光瞳内的透过率函数以采样间隔δ=4 μm进行采样,采样矩阵记为

(40)

其中,λF/δ2=1 250,各取样点的坐标为

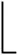
(41)

其中,R=d/δ=1 250.

考虑到像面位于透镜后2F处,计算窗口尺寸仍需取为L=10 mm.因此,需要将透镜的采样矩阵四周零填充至2 500×2 500像素,再与透镜前表面的衍射场分布矩阵进行Hadamard乘积,得到透镜后表面的光场分布矩阵U′l.再次利用角谱算法可以计算出像面上光场采样矩阵Ui.对像面光场采样矩阵Ui进行裁剪,仅保留中心1 000×1 000的矩阵元素,即为物体的像,如图7b所示.为了便于比较,图7b展示的是旋转180°之后的像.

若将像面向后移动2 mm,即像面到透镜的距离z=82 mm.这时计算窗口尺寸需要取为L=λz/δ=10.25 mm,其中采样点数为M×N=2 563×2 563.这就需要将透镜前表面的衍射场分布矩阵Ul和透镜透过率函数的采样矩阵T均四周填充至2 563×2 563,再进行Hadamard乘积得到透镜后表面的光场分布矩阵U′l.然后利用角谱算法,计算出像面光场分布采样矩阵Ui.最后对像面光场采样矩阵Ui进行裁剪,仅保留中心1 000×1 000的矩阵元素,即为物体轻微离焦的像,如图7c所示.同样,图7c展示的也是旋转180°之后的像.

由图7可以看出,利用角谱算法可以准确地数值仿真不同像距下的单透镜相干成像实验.仿真实验展示了离散物体经历级联菲涅尔衍射的计算过程.单透镜相干成像仿真实验的源程序参见开源仓库[28],以便参考.

这里通过衍射追迹的方法仿真了物体在相干照明下经过有限孔径的理想薄透镜的成像情况.然而在非相干照明下,无法通过菲涅衍射直接计算物光场在成像系统中的传播情况.但这时可以通过菲涅尔衍射计算出成像系统的相干传递函数,进而得非相干成像系统的光学传递函数,然后再利用光学传递函数得到像的强度分布[29].

3 结论

详细讨论了菲涅尔衍射积分的角谱算法,给出了算法的实施过程,澄清了理想采样条件、卷绕误差产生的原因和影响范围以及计算窗口尺寸的选取依据等相关问题.高斯光束照明余弦光栅的衍射仿真实验和单透镜相干成像仿真实验表明,按照本文给出的依据和过程执行计算,可以有效地避免应用角谱算法时出现错误,保证数值计算精度.

角谱算法和单次傅里叶变换算法[26]是2种常用的基于离散傅里叶变换的计算菲涅尔衍射积分的数值算法.在相同条件下,2种算法的计算精度基本相同,但是由于角谱算法需要进行2次离散傅里叶变换和1次矩阵Hadamard乘积运算,而单次傅里叶变换算法需要进行1次离散傅里叶变换和2次Hadamard乘积运算.因此,角谱算法花费的时间较长.以2.1节中高斯光束照明余弦光栅衍射场计算为例,角谱算法花费的时间约为单次傅里叶变换算法的1.47倍.

角谱算法基于空间滤波模型,概念比较清晰,直观地给出了卷绕误差产生的原因和影响范围.在单次傅里叶变换算法中,卷绕误差同样存在.本文给出的避免卷绕误差的方法同样适用于单次傅里叶变换算法,为从事衍射计算相关领域的研究人员提供了一个简明参考.