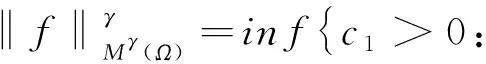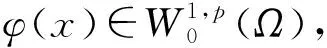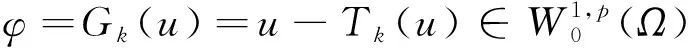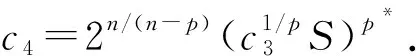一类非线性椭圆问题解的正则性

2023-06-17黄苗苗赵雪漪冯贺平

河北大学学报（自然科学版） 2023年3期

关键词：椭圆型将式有界

黄苗苗,赵雪漪,冯贺平

(1.汉江师范学院数学与计算机科学学院,湖北十堰 442000;2.湖北大学应用数学湖北省重点实验室,湖北武汉 430062;3.河北软件职业技术学院智能工程系,河北保定 071002)

设Ω为Rn(n≥2)中的有界开子集.考虑椭圆型方程的边值问题

(1)

其中,a(x,s,ξ):Ω×R×Rn→Rn和f(x,s,ξ):Ω×R×Rn→R为Carathéodory函数,对几乎所有的x∈R和所有的(s,ξ)∈R×Rn,有

a(x,s,ξ)·ξ≥α|ξ|p-k1(x)-γ1|s|θp,

(2)

|a(x,s,ξ)|≤β|ξ|p-1+k2(x)+γ2|s|n(p-1)/(n-p),

(3)

|f(x,s,ξ)|≤γ3|ξ|p-1+k3(x)+γ4|s|θ(p-1),

(4)

其中,1

k1(x)∈LT(Ω),k2(x)∈Lp′(Ω),k3(x)∈Lm(Ω),m>(p*)′,

T=[1-(1-(p*)′/m)p′/(p*)′]-1,(p*)′=(np/(n-p))′=np/(np-n+p).

(5)

为了得到椭圆型边值问题(1)在条件(2)、(3)、(4)下解的正则性,需要Marcinkiewicz空间Mγ(Ω)(也称弱Lebesgue空间)的定义,它是调和分析中的一个重要的空间,在偏微分方程解的正则性理论中应用广泛.Marcinkiewicz空间Mγ(Ω)的性质见文献[1].

定义1设γ>0,Marcinkiewicz空间Mγ(Ω)由所有满足下列条件的可测函数g:Ω→R组成:存在常数c1>0使得

g*(t)=meas{|g|>t}≤c1/tγ,∀t>0.

(6)

g∈Mγ(Ω)的范数定义为

显然,当γ>1,0<ε≤γ-1时,有

Lγ(Ω)⊂Mγ(Ω)⊂Lγ-ε(Ω).

(7)

注意到,在条件(3)和(4)下,式(7)中的积分是有限的.

非线性椭圆型方程解的正则性问题已经得到了广泛的研究,见文献[2-12],但多数考虑的椭圆型问题(1)的右端函数f只与x有关.本文考虑更复杂的一种情况,椭圆型问题(1)的右端函数f不仅与x有关,还与u(x)及Du(x)有关[13].在这种情况下,经典的Stampacchia引理[14-16]不能再使用,为了克服这个困难,需要使用推广的Stampacchia引理[17],Gao等[18]给出了稍微不同的结果,形式更为简单.

引理1设c2,α,β,k0为正常数,0≤θ<1.设函数φ:[k0,+∞)→[0,+∞)非增,且对任意k0≤k

φ(h)≤c2kθα[φ(k)]β/(h-k)α.

(8)

i) 若β>1,则存在k*>0,使得φ(k*)=0;

ii) 若β=1,则对任意k≥k0,有φ(k)≤φ(k0)exp{1-[(k-k0)/τ]1-θ},其中τ=max{k0,c2e2θα(1-θ)α};

iii)若0<β<1,则对任意k≥k0,有

下面给出本文的主要结果.

i) 若m>n/p,则u∈L∞(Ω);

ii) 若m=n/p,则存在正常数λ,使得eλ|u|1-θ∈L1(Ω);

iii) 若(p*)′