甘油连续生物歧化过程的参数辨识与非线性分析

张菁朔,徐恭贤

(渤海大学 数学科学学院,辽宁 锦州 121013)

收稿日期：2022-09-06

基金项目：国家自然科学基金资助项目(11101051);辽宁省自然科学基金资助项目(20180550839);辽宁省教育厅科学研究项目(LJ2020015)

第一作者：张菁朔(1998—),女,辽宁阜新人,渤海大学在读硕士研究生,主要从事最优化方法与应用研究.

E-mail:3480740062@qq.com

通信作者：徐恭贤(1976—),男,辽宁庄河人,渤海大学教授,博士,主要从事最优化方法与应用研究.

E-mail:gxxu@bhu.edu.cn

现如今,甘油生物歧化为1,3-丙二醇过程的参数辨识、最优控制等[1-3]生化问题受到了学者们的广泛关注.为提高1,3-丙二醇的产率,修志龙等[4]研究了以甘油为原料的连续发酵和间歇发酵过程,应用动力学模型证明了多稳态现象的发生.王宗涛[5]通过实验得到的数据及生化反应原理,建立了连续微生物发酵动力学系统的参数辨识模型.李晓红等[6]研究了微生物间歇发酵动力学系统,采用不可微优化理论得到了问题最优解.宫召华等[7]应用离散化方法将所求问题转化,并应用改进的粒子群算法求解参数.王冬妮[8]针对连续发酵生产1,3-丙二醇,建立了分数阶微生物发酵模型以及分数阶参数辨识优化问题.文献[9-11]针对微生物间歇发酵过程的动力学系统建立了不同的参数辨识优化模型,采用不同的方法求解参数值.文献[12]研究了甘油代谢过程的非线性系统的多目标优化问题.文献[13]研究了甘油生物合成1,3-丙二醇和2,3-丁二醇的最新工艺,从而使产率最大化.

在对甘油连续生物歧化过程的非线性系统进行研究时,本文采用新方法,将甘油连续生物歧化为1,3-丙二醇过程的GMA-系统稳态方程作为稳态约束,建立参数辨识优化模型,应用MATLAB序列二次规划算法[14]求解模型的最优参数值.将得到的结果与已有文献结果和应用LINGO最小二乘法求解的结果进行了比较证明方法的可行性.将辨识出的参数值回代到GMA-系统中,计算了平衡点.采用了符号化实根隔离法[15]求解出系统所有的平衡点.另外,利用线性化方法[16]对平衡点的稳定性进行了研究,并讨论了不同操作条件下的平衡点的稳定性.

1 甘油生物歧化动力系统

基于文献[17],甘油连续生物歧化为1,3-丙二醇过程的动力学系统描述如下:

(1)

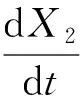
(2)

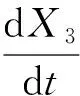
(3)

(4)

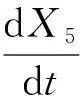
(5)

其中,t为发酵时间,X∈R5,X1为生物量,μ和D分别为细胞比生长速率和稀释速率,CS0和X2分别为初始甘油浓度和反应过程中残余甘油浓度,X3、X4、X5分别为细胞外产物1,3-丙二醇、乙酸和乙醇的浓度,qS为底物甘油的比消耗速率,qPD、qHAc、qEtOH分别表示1,3-丙二醇、乙酸和乙醇的比生成速率,μ、qS、qPD、qHAc、qEtOH表达式如下:

(6)

qS=p1+μ/p2+p3X2/(X2+p4),

(7)

qPD=p5+μp6+p7X2/(X2+p8),

(8)

qHAc=p9+μp10+p11X2/(X2+p12),

(9)

qEtOH=qS[p13/(p14+DX2)+p15/(p16+DX2)],

(10)

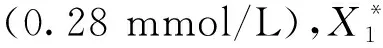
令X6=0.28+X2,X7=1-X2/2 039,X8=1-X3/939.5,X9=1-X4/1 026,X10=1-X5/360.9,X11=X2+p4,X12=X2+p8,X13=X2+p12,X14=DX2+p14,X15=DX2+p16,可以得到如下GMA-系统形式:

(11)

(12)

(13)

(14)

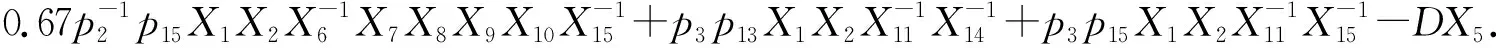
(15)

下面定义:

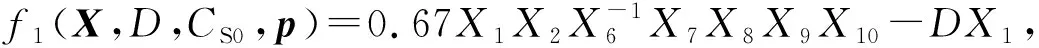
f6(X,D,CS0,p)=0.28+X2,f7(X,D,CS0,p)=1-X2/2 039,

f8(X,D,CS0,p)=1-X3/939.5,f9(X,D,CS0,p)=1-X4/1 026,

f10(X,D,CS0,p)=1-X5/360.9,f11(X,D,CS0,p)=X2+p4,

f12(X,D,CS0,p)=X2+p8,f13(X,D,CS0,p)=X2+p12,

f14(X,D,CS0,p)=DX2+p14,f15(X,D,CS0,p)=DX2+p16.

根据文献[17]的实验结果,可以得出1组经验参数值,本文将其视为参数的初始值,具体如下:

p0=(2.2,0.008 2,28.58,11.43,-2.69,67.69,26.59,15.5,-0.97,33.07,

5.74,85.71,0.025,0.06,5.18,50.45)T.

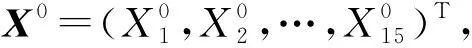
(16)

其中,Pad为R16中的有界闭集,由此可以得到系统(16)的如下性质:

性质1设p∈Pad,Pad为R16中的有界闭集,则函数fi(X(t),D,CS0,p)在区间[t0,tf]上连续可微,即fi∈C1([t0,tf];R15),且fi关于p∈Pad连续.

性质2若p∈Pad,则非线性动力学系统(16)存在唯一解X(·;p),且X(·;p)在Pad上关于p连续.

对于X0,定义系统(16)的解集S(X0)为

S(X0):={X(·;p)∈C([t0,tf];R15)|X(·;p)为系统(16)对应p∈Pad的解}.

(17)

根据允许集Pad定义,Pad为R16中的有界闭集,从而为紧集.由性质1和性质2可知,从p∈Pad到X(·;p)∈S(X0)的映射是连续的.可以得到如下性质:

性质3集合S(X0)是C1([t0,tf];R15)中的紧集.

2 参数辨识优化模型

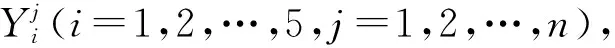
qS(Xj,p)≥0,j=1,2,…,n,qPD(Xj,p)≥0,j=1,2,…,n,qHAc(Xj,p)≥0,j=1,2,…,n,

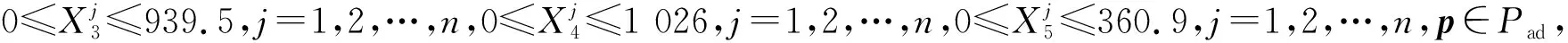
性质4甘油连续发酵过程GMA-系统的参数辨识优化模型存在最优解p*,即存在p*∈Pad,使得对于任意p∈Pad,都有J(p*)≤J(p).

3 参数辨识结果

本文选取文献[17]中21组实验稳态数据.为求解参数辨识优化模型中的参数,选用最优化算法中的序列二次规划算法[14],令Pad={p∈R16|pa∈[0,100],pd∈[-100,0],a=1,2,3,4,6,7,8,10,…,16,d=5,9}.参数辨识结果如表1所示,计算值误差对应表2的本文方法误差.此外,本文还建立了以动力学系统(1)～(5)等号右端的平方和为目标函数的参数辨识优化模型进行对照,并应用LINGO软件最小二乘法求解得到的参数辨识结果如表1所示,计算值误差对应表2的LINGO计算误差.表2为本文方法误差和已有文献的误差的比对结果,其中误差函数的数学定义式如下:

表1 参数辨识结果

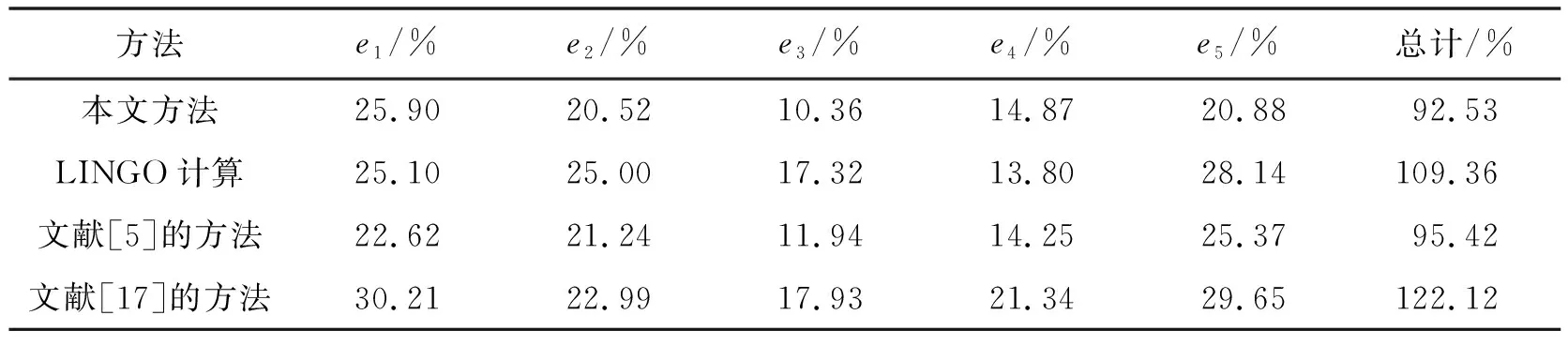
表2 误差比较

(18)

通过表2的误差比较可知,应用甘油连续生物歧化过程的GMA-系统,建立以模型计算值与实验测量值误差最小为目标函数的参数辨识优化模型产生的浓度误差小于已有文献[5,17]的计算误差.

4 系统平衡点的数值计算

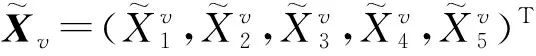
(19)

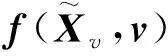
性质5对任意的v=(CS0,D)∈Vad,系统至少存在1个平衡点.

图1为GMA-系统中的生物量X1、甘油浓度X2、1,3-丙二醇浓度X3、乙酸浓度X4和乙醇浓度X5在稀释速率D为0.1 h-1、0.2 h-1和0.3 h-1时的计算结果.当稀释速率D不变时,随着初始甘油浓度CS0增大,GMA-系统的平衡点个数发生了变化.以稀释速率D为0.1 h-1的情况为例,随着CS0逐渐增大,生物量X1、甘油浓度X2、1,3-丙二醇浓度X3、乙酸浓度X4、乙醇浓度X5先是出现了1个平衡点,接着出现了2个平衡点.

a.生物量X1;b.甘油浓度X2;c.1,3-丙二醇浓度X3;d.乙酸浓度X4;e.乙醇浓度X5图1 不同稀释速率下的平衡点计算结果Fig.1 Calculation results of equilibrium points at different dilution rates

5 系统平衡点的稳定性分析

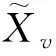
(20)

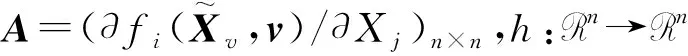
(21)

(22)

(23)

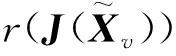
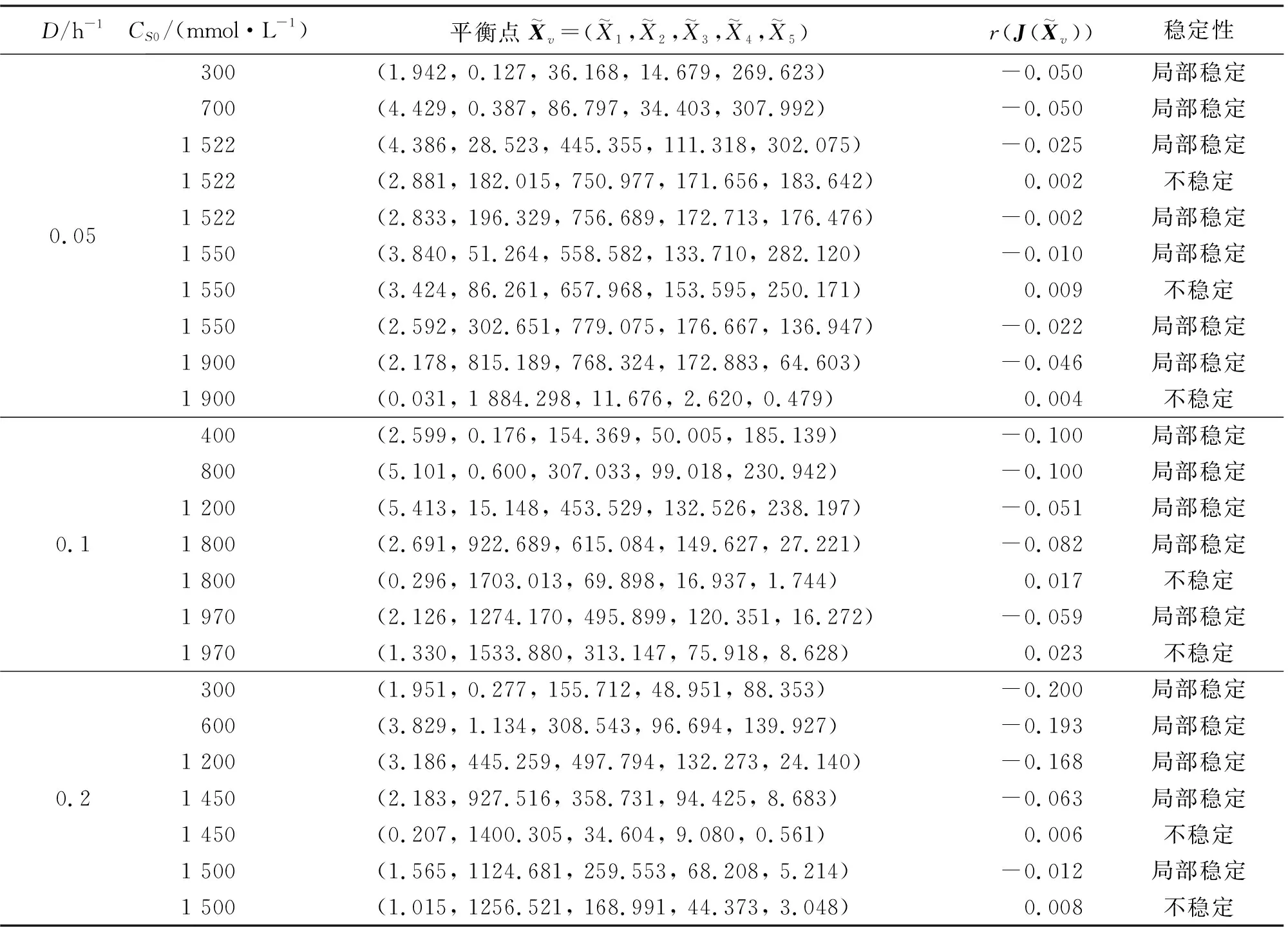
表3 不同D和CS0情况下的平衡点数值解及其稳定性

6 结论

针对甘油连续歧化为1,3-丙二醇过程的非线性GMA-系统进行了研究,构建了包含甘油连续发酵过程GMA-系统的稳态方程为约束的非线性参数辨识优化问题.与已有的参数估计方法和应用LINGO最小二乘法求出的参数相比,本文应用序列二次规划算法得到的最优参数值误差更小.针对GMA-系统进行了非线性分析,通过第1步求解出的参数值,根据符号化实根隔离法求解出不同操作条件下生物系统的全部平衡点,给出了不同稀释速率下的平衡点分布情况.应用几乎线性系统的稳定性理论分析了GMA-系统平衡点的稳定性,选取了3种不同稀释速率下的平衡点的数值进行了稳定性分析.