液氢中固空枝晶生长凝固定量相场法研究

李超龙,文键,王磊,厉彦忠,,雷刚,屠基元

(1.西安交通大学能源与动力工程学院,710049,西安; 2.航天低温推进剂技术国家重点实验室,100028,北京; 3.皇家墨尔本理工大学工学院,VIC 3083,澳大利亚墨尔本;4.清华大学核能与新能源技术研究院,100084,北京)

面对日益严峻的气候问题,清洁低碳的氢能是一种备受青睐的替代能源[1]。其中,液氢液氧组合的推进剂是大推力火箭发动机的理想选择[2]。然而,由于液氢的低温特性,暴露于液氢的空气会迅速冻结,包裹于液氢中的固空颗粒在微弱能量的激发下存在爆炸风险。此外,固空的积聚沉积容易堵塞细小的管道和阀门,使得火箭发动机燃烧不稳定。Cassutt等[3]利用熔丝引爆300 g固空和4.73 L液氢的混合物,发现固空中的氧含量是引发爆炸的关键因素;以枪击的形式引爆,能够引起液氢爆炸的固空氧含量最低为24%;当与惰性气体共存时,该值提升至40%。由于溶解度的差异,冻结的固体空气中氧溶质的分布并不均匀。刘海生等[4]等研究了固空在液氢中的沉积现象,发现固空呈现雪花状。此外,通过测量升温过程氧氮逸出质量分数发现固空颗粒表面富氧,内部贫氧的氧溶质分布特征。然而,这些实验未能得到固空枝晶的全过程生长图像,也未能直接得到枝晶生长凝固过程中枝晶内部和液相中氧溶质的分布。

考虑到液氢的低温及不稳定性,通过实验手段获得固空枝晶微结构演化和溶质分布信息是相当具有挑战的。幸运的是,数值模拟方法如元胞自动机(CA)、相场法等已成为复现枝晶凝固微观结构演化的有效手段[5-10]。课题组在先前的研究[11-12]中运用格子玻尔兹曼和元胞自动机耦合方法初步探索了固空枝晶生长凝固行为,但所得到的固空枝晶形态较为简单,仅包含一次枝晶臂,并不能反映真实固空枝晶微观结构。相场模型不需要明确追踪移动界面,弯曲枝晶界面对枝晶生长动力的贡献即Gibbs-Thomson效应可以被精确表达。得益于众多学者的巨大努力,相场模型取得了显著进展[13-16]。Karma等[15]基于薄界面限制定量模拟了纯质的等轴枝晶生长,在此基础上,该模型陆续被拓展到二元和多元组分系统的凝固行为的定量模拟。Rojas等[17]采用相场结合格子玻尔兹曼法探究了对流存在下枝晶的生长凝固行为。Nabavizadeh等[18]使用相场法对微重力条件下琥珀腈溶液的枝晶生长的实验数据进行了验证,得到的枝晶尖端生长速度与实验符合良好。由于具有六重对称性的固空枝晶微观结构演化[19]及氧溶质分布对于液氢系统的安全至关重要,在完善先前研究不足的动机下,我们致力于开发能够复现固空枝晶真实形态的定量相场模型。

为了探究液氢中固空枝晶生长凝固特性,本文建立了二维定量相场模型,且为提高数值求解过程的稳定性,对相场序参量进行了非线性预处理,研究了连续冷却条件下固空单枝晶和多枝晶微观结构演化和氧溶质分布规律,可为液氢系统的安全使用提供理论指导。

1 数值模型与求解

1.1 定量相场模型

本文将空气简化为仅含有氧气和氮气的二元组分,空气降温后形成成分均匀的二元溶液,氧溶质的质量分数为0.233。采用完善的定量相场模型探究固空枝晶微结构演化过程和溶质偏析现象,可以在固液界面厚度W0大于毛细长度d0的条件下保持定量特性。由于空气溶液的热扩散系数高出溶质扩散系数两个数量级,计算域中的温度梯度忽略不计,并且不考虑凝固潜热,因此具有恒定冷却速率的空气枝晶等温凝固,其计算域内温度场表述为

T=Tint-RDt

(1)

式中:Tint是初始温度;RD是冷却速率,当RD=0时计算域保持初始温度,即空气溶液具有恒定过冷度;t是时间。

连续场φ被用于描述与空间和时间对应的相,对于固相,φ=1,对于液相,φ=-1,在固液界面区域,φ在-1和1之间光滑地变化。为了使相场变量φ在较大网格下的时间演化中保持数值稳定,相场φ的本构方程通过非线性预处理的定量相场ψ重新定义

(2)

非线性预处理定量相场ψ的演化方程为

(3)

无量纲氧溶质场U的扩散方程为

(4)

其中

(5)

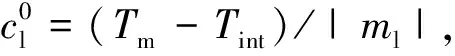
(6)

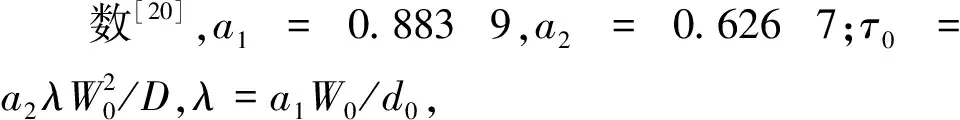
(7)

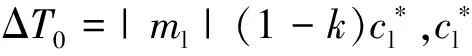
(8)

当Ω=1时,方程(8)退化为方程(7)。as(n)是表征枝晶各向异性的函数,对于具有六重对称性的固空枝晶的二维计算,as(n)表达式[21]如下

as(n)=1+ε1·

(9)

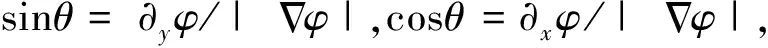
as(n)=as(θ)=1+ε1cos[6(θ-θ0)]

(10)

式中:θ0是相对于x轴的晶体取向角度,当θ0=0°时,方程(10)和方程(9)等效。

1.2 模型数值求解

定量相场模型在x和y方向的空间离散均采用具有固定步长Δx的有限差分方法,其在时间域的演化采用欧拉显式时间方案,时间步长为Δt。空间和时间分别以固液界面厚度W0和松弛时间τ0为单位进行缩放。对于具有六重对称性的固空枝晶,当规则笛卡尔正交网格被用于定量相场模型(QPFM)的有限差分离散时,虚假网格各向异性的引入不可避免地影响了枝晶尖端的生长动力[22],对于具有不同生长取向的多枝晶生长凝固过程,这种影响尤其明显。实际上,在无其他因素干扰时,不同取向的固空枝晶生长形态应具有旋转不变性。要保持枝晶生长的旋转不变性,方程(3)和(4)的离散要求最大化地保持各向同性。为达到这一目的,本研究采用了Ji等[23]提出的一种基于两个基础离散基的线性组合来保持笛卡尔网格中各向同性化离散的有限差分法。相场φ通过预处理相场ψ的演化获得,当|ψ|≥10.27时,|1-φ|≤10-6,此时认为处于单一均匀相。对于单枝晶计算,相场模型四周边界采用零扩散Neumann边界;对于多枝晶计算,则四周采用周期性边界。计算初始在计算域中放置晶核并赋予枝晶取向角,对于多枝晶,不同枝晶的取向角可以是随机的。对于具有不同枝晶生长取向角的多枝晶计算,在保持一个唯一相场φ的条件下,引入一个枝晶取向场P用于记录当地的枝晶取向角,而当地的枝晶取向角继承与其距离最近的固空枝晶。采用的模型参数及物性参数见表1。

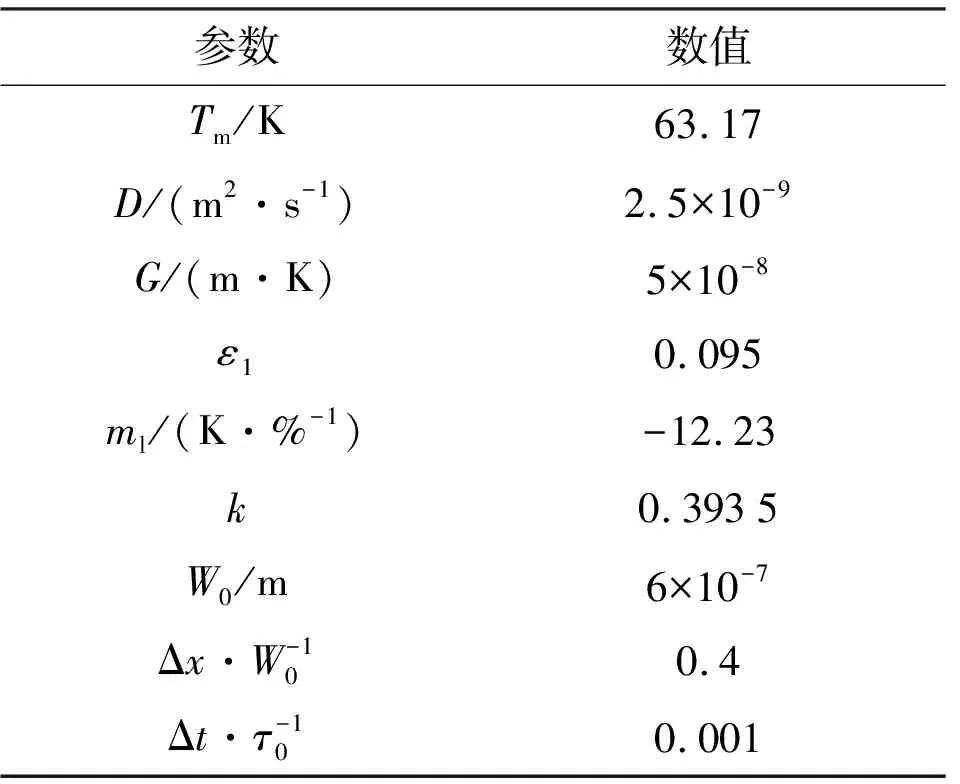
表1 模型参数及物性参数[24]

2 计算结果及分析

2.1 自由枝晶生长:与解析理论的对比

由于空气枝晶的尺度微小和液氢的低温特性,因此难以获取固空枝晶生长的直接实验数据,考虑与解析理论对比来验证相场模拟的可靠性。流行的枝晶生长解析理论一般通过形态稳定性分析和溶解性理论得到枝晶稳态生长模式与过冷度之间的关系。Ivantsov第一个提出了描述控制枝晶生长的过冷度ΔT与枝晶生长Pélect数Pc之间的关系的枝晶稳态生长解析理论并定义了Ivantsov函数。Pc=vtipρtip/2D,vtip是尖端生长速度,ρtip是尖端曲率半径。尖端速度vtip通过记录尖端位置获得,而尖端曲率半径则通过尖端轮廓文件拟合得到。Alexandrov等[25]将六重对称枝晶的各向异性考虑在内推导了决定vtip和ρtip的选择标准并给出了修正的Ivantsov函数

(11)

对于2D计算,方程(11)中j取2,过饱和度Ω与Pc的关系可定义如下

(12)

图1展示了不同无量纲过冷度下过饱和度Ω与Pc之间的依赖关系,红色虚线代表解析理论预测结果,而散点数据为当前QPFM模拟结果。可以看到,当前模拟与解析结果相对误差范围为-3.75%～4.33%,表明两者取得了良好的匹配性。

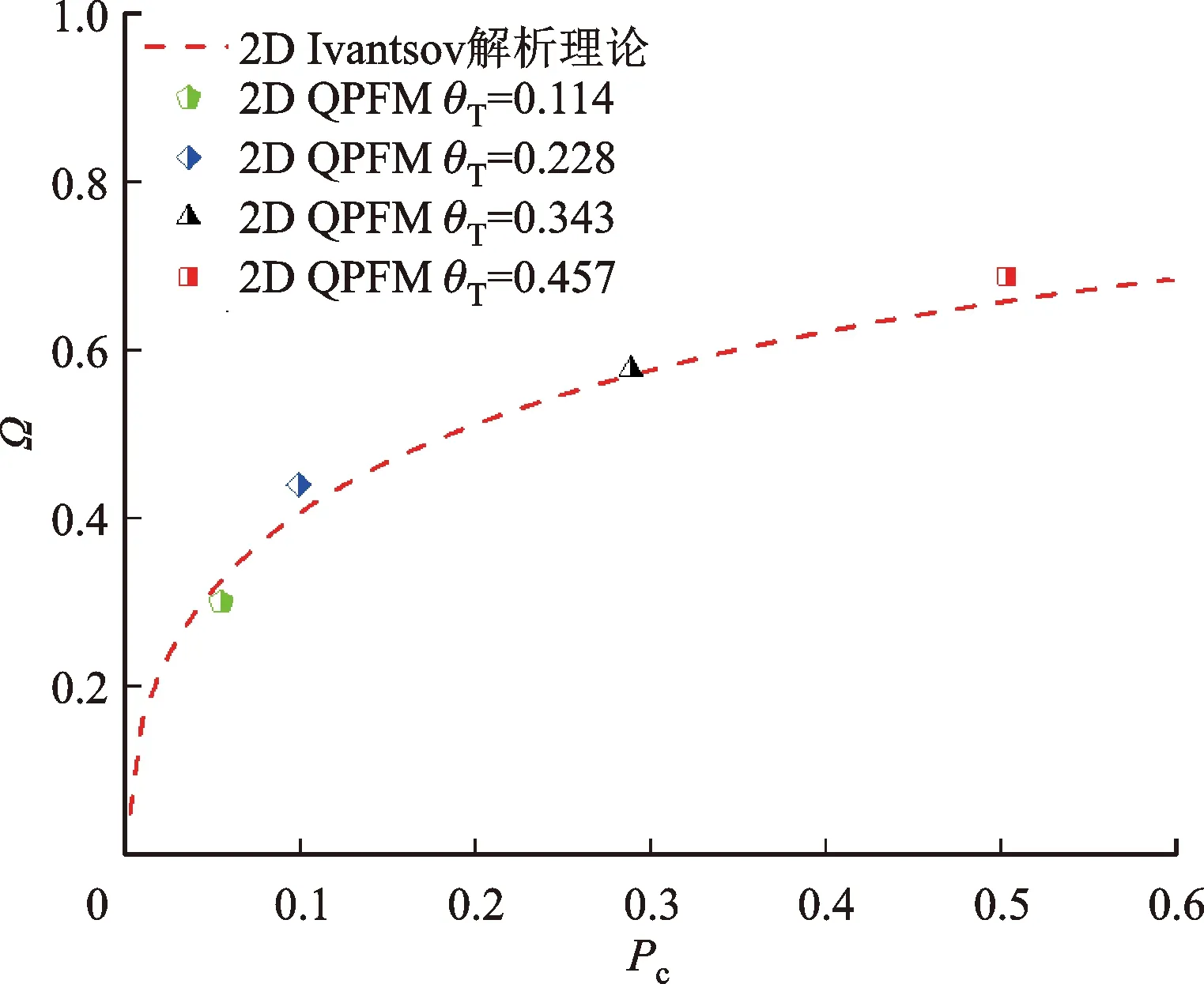
图1 过饱和度Ω与Pc的依赖关系:当前模型与解析理论的对比

2.2 单枝晶生长:初始过冷度的影响

本节研究初始过冷度对固空枝晶形态演化和氧溶质分布的影响,并选择两条特殊位置曲线定量表述氧溶质分布规律。对于所有案例,计算区域网格为设定为500×500,经过无关性检验,网格步长选定为Δx=0.4W0。计算域初始氧溶质质量分数c0=0.233,半径r=115d0的圆形晶核被置于计算域中心,晶核内氧质量分数为kc0,枝晶生长取向角θ0=0°。冷却速率保持RD=10 K/s,时间步长Δt=0.001τ0,模拟持续20 000步。

图2(a)～(d)左半边展示了20 000Δt时刻不同初始过冷度(1.0、1.5、2.0、2.5 K)下固空枝晶的形态。可以看出,不同初始过冷度下固空枝晶均呈现六重对称雪花形态,但在初始过冷度为1.0 K时仅分化出少量的二次枝晶臂,枝晶二次枝晶臂随初始过冷度增大而更加发达,枝晶形态复杂度增加。

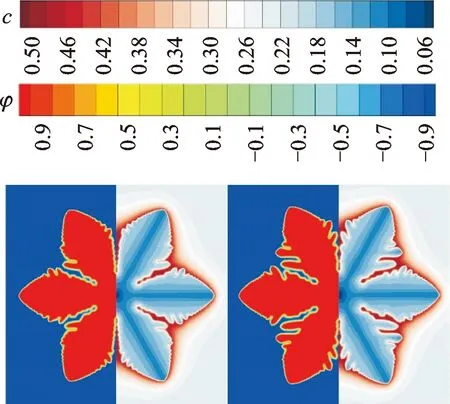
(a)1.0 K (b)1.5 K

图2中右半边则展示了20 000Δt时刻不同初始过冷度下氧溶质质量分数分布情况,可以明显看到,氧溶质质量分数分布呈现枝晶内部贫氧外部富氧的分布特征。对于不同初始过冷度,氧溶质质量分数在固液界面附近达到最大并高于初始质量分数(0.233),而固空枝晶内部氧溶质则低于初始质量分数,这与早前的实验结果[4]相符合。随着初始过冷度的增加,固空枝晶二次枝晶臂更为发达,二次枝晶臂的存在不利于氧溶质及时的向外扩散,在枝晶臂的间隙位置氧溶质积聚从而导致了更高的氧质量分数。

图3展示了枝晶尖端生长速度和固相率Fs(固体元胞占计算域元胞比例)随时间的变化。固相率随时间增长一直增加并且由于二次枝晶臂的发展固相率后期的增加速率变快,同一时刻,固相率随初始过冷度增加而变大。在18 000Δt时刻固相率由初始过冷度1.0 K的0.222增加到2.5 K的0.301。初始时刻,不同初始过冷度下枝晶尖端均具有一个较高的生长速度,随着凝固的进行枝晶尖端生长速度逐渐降低并达到稳定阶段。稳定阶段的枝晶生长速度随过初始冷度增加而增大,初始过冷度由1.0 K增加到2.5 K时,固空枝晶尖端速度由0.364 mm/s增长到0.673 mm/s。

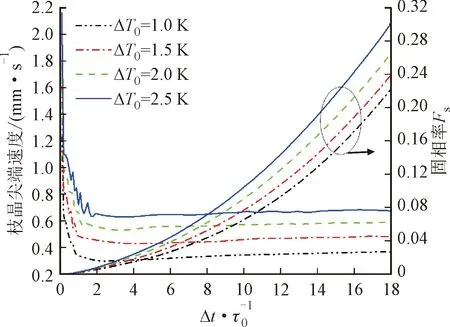
图3 枝晶尖端速度和固相率随时间的变化

由于溶解度的差异,固空枝晶生长过程中会发生氧溶质再分配现象。固体空气中氧溶质的溶解度较低,因此固空枝晶凝固生长时部分氧溶质会被释放到液相中形成溶质偏析现象。尽管课题组之前的研究建立了数值模型来研究固空枝晶的这种溶质偏析现象,但固空枝晶的形态被简化,模型的定量能力不足[11-12]。接下来,将选取两条特殊曲线位置着重以定量的形式揭示QPFM得到的固空枝晶生长凝固过程中的氧溶质分布规律。

图4展示了20 000Δt时刻不同初始过冷度下沿计算域水平中线(L1线)的相场和氧溶质质量分数分布。可以看到,相场参数数值在中心区域保持1(固相),而在两边区域保持-1(液相)不变,数值突变区域即为固液糊状区,固液界面即固空枝晶尖端具体位置以φ=0等值线对应位置确定,由于生长速度的差异,枝晶尖端到边界的距离有所不同。在固空枝晶核心区域,氧溶质质量分数由内向外逐渐升高,当氧溶质质量分数达到0.111时,固空枝晶开始从核心区域分化出一次枝晶臂。不同初始过冷度下沿与P1线重合的一次枝晶臂其晶轴氧溶质质量分数几乎保持恒定且只表现出微弱的差别。由于氧溶质的释放,氧质量分数在糊状区陡然升高,糊状区氧质量分数峰值和初始过冷度呈现正相关,值得注意的是,氧质量分数峰值出现的位置并非固液界面处。当初始过冷度为1.0、1.5、2.0、2.5 K时,糊状区氧溶质质量分数峰值Cm分别为0.402、0.407、0.425、0.469,而固液界面处氧溶质质量分数Ci分别为0.265、0.268、0.280、0.313,均高于初始质量分数0.233。

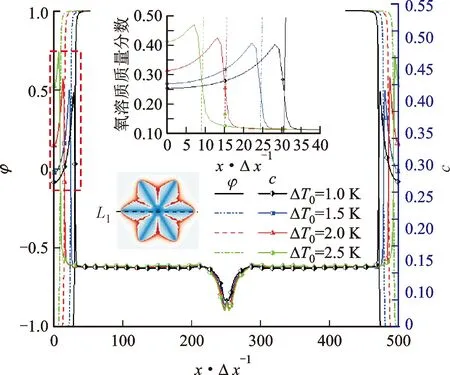
图4 不同初始过冷度下沿L1线相场和氧溶质分布

由于沿一次枝晶臂和二次枝晶臂的轴线形成了氧溶质质量分数较低的脊柱(图2)。为了全面描述氧溶质分布规律,图5给出了沿红色虚线圆弧C1(以枝晶中心为圆心,半径R=190Δx)的氧溶质质量分数分布,角度θ范围为150°～210°。可以看到,不同初始过冷度下自一次晶轴方向(180°)向两侧,氧溶质质量分数逐渐升高,并在固液界面附近达到峰值。当初始过冷度为1.0、1.5、2.0、2.5 K时,氧溶质质量分数峰值Cm分别为0.433、0.449、0.466、0.488。对于初始过冷度2.5 K,氧溶质质量分数分布曲线出现多个波谷,这是因为此时枝晶有着发达的二次枝晶臂,这些波谷即对应二次枝晶臂轴线位置。

2.3 多枝晶生长:冷却速率的影响

应用QPFM对多枝晶在连续冷却条件的生长演化进行了研究。初始过冷度为ΔT0=1.0 K,冷却速率分布设置为2、5、10、15 K/s,其他条件与上节保持相同。

图6展示了不同冷却速率下固空枝晶形态随时间的演化,冷却速率分别为2、5、10、15 K/s,第一列到第4列对应的时刻分别是4 000Δt、15 000Δt、30 000Δt、45 000Δt。初始阶段,各枝晶之间距离较远,相互之间几乎没有影响,各枝晶沿各自取向发展并形成一次枝晶臂。随着时间的增长,一次枝晶臂逐渐长大并开始分化出二次枝晶臂,不同枝晶的枝晶臂开始接近并影响了枝晶臂的原有生长轨迹,位于中心的枝晶的生长受到明显抑制。在连续冷却条件下,二次枝晶臂随时间增加持续续粗化、融合,对于冷却速率RD=15 K/s,枝晶最后几乎充满了计算域。

图7展示了不同冷却速率下固相率随时间的变化,可以看到固相率随时间增长而增大,并且更大的冷却速率对应的固相率更高。连续冷却条件下,在30 000Δt时刻之后固相率仍持续增长但增长率降低。在60 000Δt时刻,当冷却速率分别为2、5、10、15 K/s时,固相率Fs分别为0.446 0、0.658 5、0.830 5、0.911 1。图8展示了与图6相对应的连续冷却条件下多枝晶氧溶质质量分数分布。同样地,枝晶生长初期因各枝晶间距离较远,氧质量分数分布不受其他枝晶干扰。随着时间的增长,枝晶臂开始接近并形成间隙,枝晶凝固生长过程排出到液相的氧溶质积聚在枝晶臂间隙中,使得局部的饱和度增加从而抑制了当地枝晶臂的发展。图9给出了不同冷却速率下计算域内氧溶质质量分数最大值随时间的变化情况。可以看到,计算域内氧溶质质量分数最大值随时间几乎呈现线性增长趋势增长率随冷却速率增大而增大。在45 000Δt时刻,当冷却速率分别为2、5、10、15 K/s时,氧溶质质量分数最大值Cm分别为0.387 6、0.491 9、0.668 4、0.840 6。

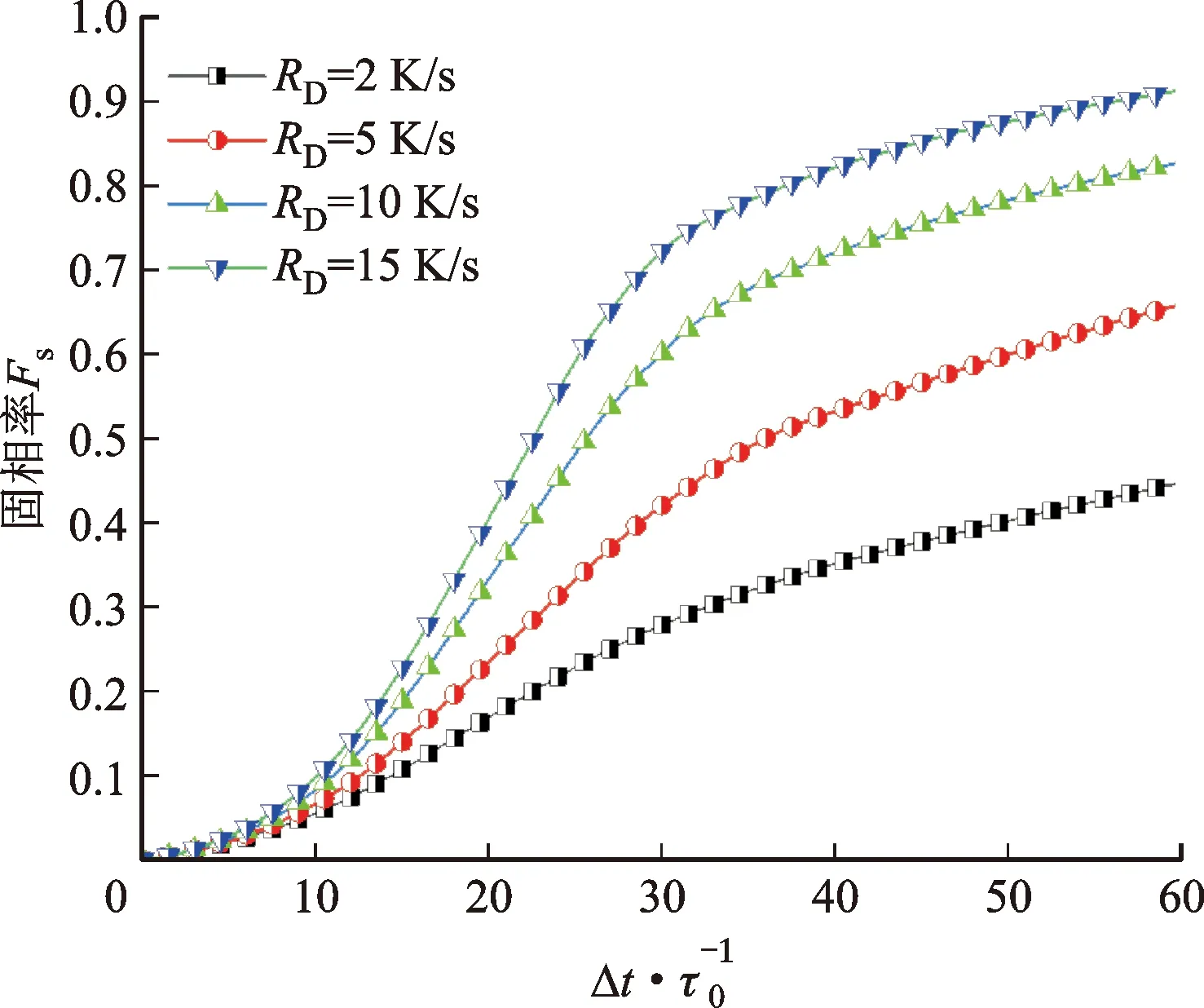
图7 不同冷却速率下固相率随时间的变化

(a)2 K/s

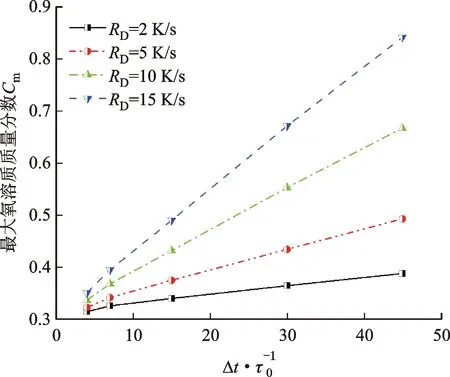
图9 不同冷却速率下最大氧溶质质量分数随时间的变化

3 结 论

本文建立了经过非线性预处理的定量相场模型,着重对单枝晶和多枝晶在连续冷却条件的生长凝固行为进行了研究;获得了固空枝晶形态的瞬态演化和定量氧溶质分布,增进了液氢中固空枝晶生长行为的理解,对液氢系统安全使用具有一定参考意义,主要结论如下。

(1)氧溶质质量分数总体呈现枝晶内部含氧量低外部含氧量高的分布特征,在一次枝晶臂和二次枝晶臂轴线上形成低氧溶质质量分数脊柱。

(2)固空枝晶尖端生长速度随初始过冷度的增加而增大,并且二次枝晶臂更为发达,形态变得复杂。当初始过冷度由1 K增加到2.5 K时,固空枝晶尖端速度由0.364 mm/s增长到0.673 mm/s。

(3)多枝晶生长时固空枝晶的对称性被破环;连续冷却条件下,固空枝晶二次枝晶臂随时间增长逐渐粗化、融合,最终充满计算域,计算域内氧溶质质量分数最大值随凝固进行持续升高,氧溶质质量分数在晶界位置达到最大值。冷却速率由2 K/s升高到15 K/s,氧溶质质量分数最大值由0.387 6升高到0.840 6。

考虑到固空枝晶生长过程可能受外界热力环境影响,将包含凝固潜热在内的能量方程耦合到当前模型即进行非等温相场模拟是未来进一步的研究方向。