灯泡贯流泵水力性能和鱼类通过性能的多目标优化研究

2023-06-15叶晓琰吴跃虎潘强张德胜孙龙月施卫东

西安交通大学学报 2023年5期

叶晓琰,吴跃虎,潘强,张德胜,孙龙月,施卫东

(1.江苏大学流体机械工程技术研究中心,212013,江苏镇江; 2.南通大学机械工程学院,226019,江苏南通)

南水北调工程作为举世瞩目的跨流域调水工程,其东线工程是世界上规模最大的梯度泵站工程[1]。2020年,南水北调东线二期工程规划黄河以南干线输水梯级泵站共14座,其中约 1/3 为贯流泵装置[2]。目前,我国大中型泵站贯流泵机组通常不考虑鱼类通过性能,在鱼类资源丰富的流域,泵叶轮旋转工作时易造成鱼类大面积死亡,不仅对局部水域造成污染,同时会影响鱼类自然生态系统[3]。

历年来,学者们在生态友好型水力机械方面进行了大量研究,发现造成鱼类损伤和死亡的主要因素是压力波动、流体剪切力和机械损伤[4-5]。Van Esch等[6-7]的研究表明,在扬程低于8 m的泵站流道中,压力波动和速度剪切在大多数时候并不会对鱼造成致命威胁,叶片前缘撞击才是造成鱼类死亡的主要因素。Amaral等[8]通过实验发现,半圆形且加厚的叶片前缘可以增强鱼的偏转,提升鱼类存活率。Hogan[9]通过短时间内迅速降压的方式发现不同鱼类可承受的压降不同,有鱼鳔的鱼类存活率远高于无鱼鳔的鱼类。文献[10]进行了大量的数值计算和活鱼实验,评估叶片前缘厚度、前缘截面形状对鱼类存活率的影响,结果表明,叶片前缘越厚,鱼类的形变程度越大,可以更大程度上减弱与叶片直接接触时的撞击力。潘强[11]采用幂函数描述前缘前掠形状函数,得到了不同前缘轮毂比和前掠度下限制水平撞击速度的最优指数,可作为鱼类友好型轴流泵叶片前缘形状的设计依据。Amaral等[12]对比了传统涡轮叶片与前缘弯掠叶片在活鱼实验中的表现发现,前缘弯掠设计有助于提升鱼类经过中高速涡轮机时的打击存活率。

近年来,随着优化算法的兴起,学者们逐步尝试将这种技术应用到工程中去,并取得了良好结果。Zhang等[13]提出了一种由响应面模型和遗传算法组成的优化系统,对抽水蓄能电站垂直管道进、出口参数进行分析及性能优化,结果表明,其总水头损失系数降低了4.69%,进、出流速分布系数分别降低了11.76%和38.59%。刘小民等[14]将离心叶轮参数化方法、多目标遗传算法与数值计算软件相结合,建立了离心叶轮自动优化平台,以总压比和效率为设计目标,对高速离心叶轮进行优化,优化后叶轮出口截面上流场分布更加均匀,总压比和等熵效率约提高了2.5%和1.0%。王梦成等[15]采用由反问题设计法、Kriging模型、非支配遗传算法相结合的方法,选取混流泵在0.7Q和1.1Q工况下的效率作为优化指标进行多工况优化,优化后的模型在较大流量范围内的泵段效率均有明显提升。卢金铃等[16]针对三元扭曲叶片优化设计变量较多的问题,提出一种反问题与神经网络相结合的新方法,减少设计变量的同时大大缩短了计算时间,并利用该方法对混流泵扬程及效率进行优化,优化后叶片性能得到改善。

目前,大型水力机械研究多以提升水力性能为目的,而综合考虑水泵性能指标和鱼类损伤的多目标优化研究却少有关注[11]。对叶片式轴(贯)流泵而言,提升鱼类通过性能的措施往往与改善水力效率的措施背道而驰,如何兼顾两者,是我国大型泵站群向生态水利方向发展的技术难题。

本文以南水北调工程某泵站水力模型为原型,基于敏感度分析实验、最优拉丁超立方抽样、Kriging模型及NSGA-Ⅱ算法,构建多目标优化系统,得到综合考虑水泵性能指标和鱼类损伤指标的多目标寻优方案,分析各设计参数与水泵性能和鱼类存活率之间的关联,为大型泵站鱼类友好型优化设计提供参考。

1 计算模型及数值方法

1.1 水力模型

本文优化对象以南水北调工程某泵站模型为原型,流体区域包括以下5个部分,分别为进水流道、叶轮、导叶、灯泡体、出水流道、延伸段,如图1所示。多目标优化旨在改善鱼类通过性能的同时维持泵的水力性能达到原型要求。本文在额定工况点下对原型叶轮进行生态友好型初步设计,两者三维模型及详细参数见图2和表1。

表1 模型泵详细参数

图1 贯流泵模型计算域

(a)原型叶轮 (b)生态友好型叶轮

1.2 数值模拟及网格无关性论证

本文采用CFX进行数值模拟,为模拟泵内不可压缩流动,借助剪切应力输运湍流模型k-ωSST求解控制方程,采用压力入口与质量流量出口来描述进出口边界条件,泵内所有物理界面均采用无滑移壁面,利用二阶离散格式,收敛精度为10-6。非定常计算中,以叶轮旋转3°作为一个时间步长,在流场监测参数达到相对稳定后,采用最后一个周期的数据进行非定常流动特性分析。

所用模型的详细网格结构如图3所示。为捕捉近壁面流动状况,通过边界层加密的方式进一步提升模拟准确性,其中叶轮与导叶作为关键部件,其平均y+均小于10。

(a)叶轮域

为验证网格独立性,分别生成了6组网格,如图4所示,当网格节点数从931万增加到1 413万之后,效率值趋于平稳且始终在0.15%以内波动,扬程曲线的波动也很小。为了在保证模拟精度的前提下减少计算资源,本研究中初始模型和优选模型采用非定常计算,且网格数均保持在1 413万左右,优化过程抽样所得125组模型采用定常计算,并将进出水流道简化成圆管,控制网格数量至900万左右。

图4 网格无关性论证

1.3 实验验证

对原型泵水力模型进行外特性实验,以验证本文数值模拟方法的准确性。该模型的外特性实验在江苏大学国家水泵及系统工程技术研究中心水力机械四象限实验台上进行,图5为该实验台平面图,图6为实验台实物图。

1—高压罐1;2—高压罐2;3—电机;4—测试泵;5—低压罐;6—蝶阀;7—电磁流量计;8—循环泵。

图6 本文模型外特性实验台实物图

在实验过程中,扬程由压差传感器测量(型号为EJA110A,误差为±0.1%),流量通过电磁流量计测量(型号为OPTIEFUX2000F,误差为±0.1%),采用转矩转速测量仪测量输入功率(型号为NJ L2,误差为±0.1%),实验台系统的综合不确定度小于等于0.3,详见文献[17]。实验所得外特性曲线与数值模拟结果如图7所示,其中Qd为标准工况下流量。图中Qd为设计工况下的流量,可以看出,模拟与实验所得曲线趋势一致,在设计工况点的扬程误差为4.1%,效率误差为2.8%,非设计工况点模拟与实验值最大偏差均小于5%,数值计算结果与实验结果的吻合度较高。

图7 外特性模拟曲线与实验曲线

1.4 叶片撞击模型

叶片撞击模型自Von Raben[18]首次提出后,被大量应用在水力机械中进行鱼类损伤的理论预测。应用此模型可在短时间内定量估算出不同类型泵在多种条件下的鱼类通过性能。文献[19]提出了一种预测轴流泵不同致损因素导致的鱼类损伤概率,并通过实验验证了该准则的准确性;文献[6-7]建立并通过实验验证了轴流泵叶片撞击模型,并提出一种鱼类损伤的相似准则,可以在泵的整个运行参数范围内换算鱼类死亡率;文献[20]提出了一种叶片撞击模型,该模型结合并修正了Van Esch和Krakers的预测模型,并与活鱼实验的结果进行了对比验证,如图8所示,该模型在10组工况下的预测值与实验值之间具有较好的一致性。因此,本文采用Pan提出的叶片撞击模型来预测鱼类死亡率,以鱼体通过叶片进口处过流断面所需时间tf与叶片通过时间tb表征叶片撞击概率,即

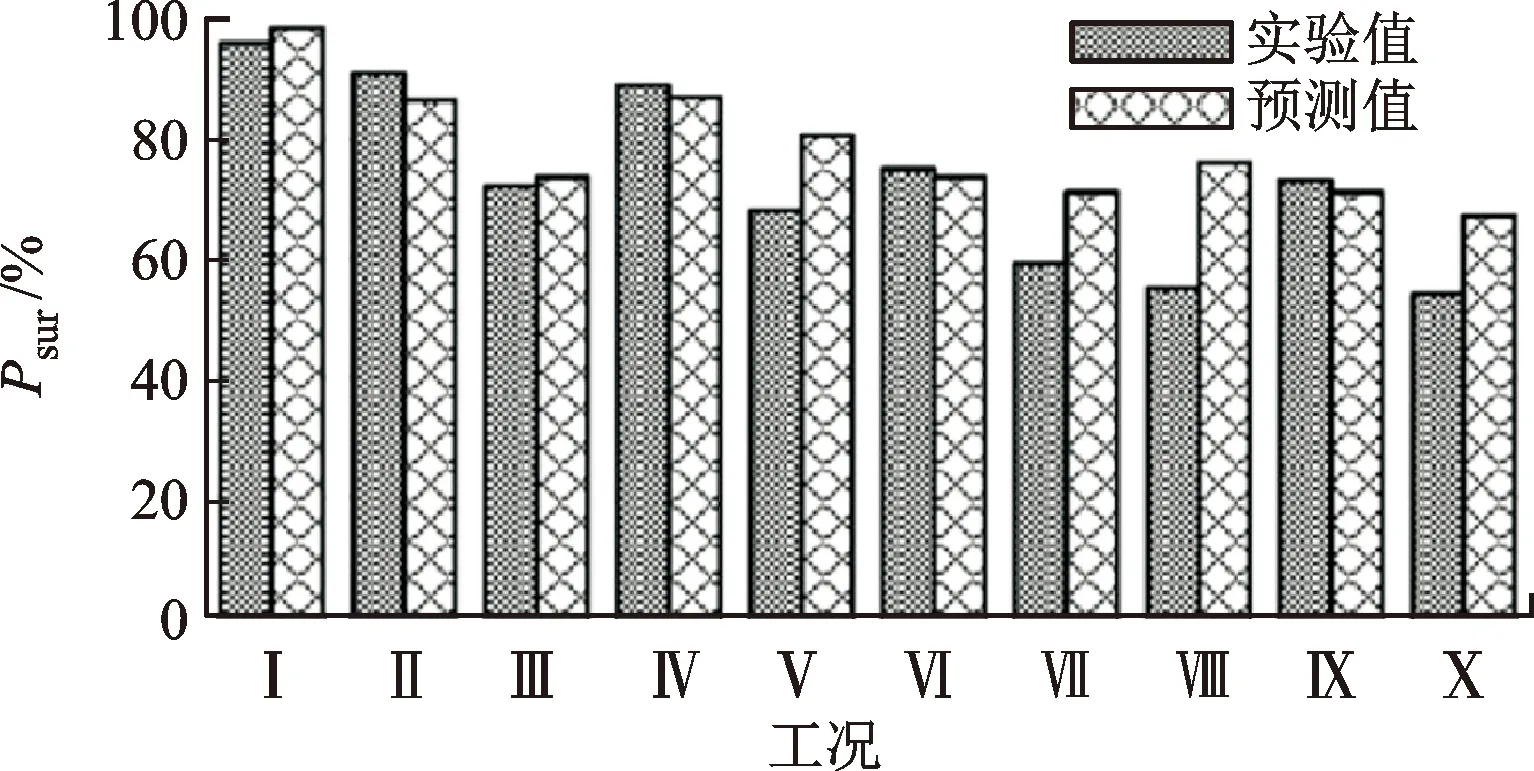
图8 本文预测值与活鱼实验结果对比

(1)

式中:Pth为叶片撞击概率;kf为修正系数;Lf为鱼长;A1为过流断面面积;ni为叶轮叶片数;N为转速。

采用fm表征鱼类受到叶片前缘撞击后的死亡比率,即

(2)

式中:a1、b1为系数;d为叶片前缘厚度;vs为撞击速度。

该预测模型本质是叶片撞击概率与撞击死亡率的乘积在半径方向的面积分,即

(3)

式中:Psur为鱼类存活率;R1h为轮毂半径;R1t为轮缘半径。

2 多目标优化设计系统

本优化系统包括三维参数化设计、敏感度分析、计算流体动力学、实验设计、近似模型、非支配遗传算法等,优化流程如图9所示。

图9 本文多目标优化设计系统流程

2.1 参数化

大量学者研究得到了影响叶轮水力性能的主要几何参数[21-25],基于此,本文选取参数L2、L3、ihub、ishr、rhub、rshr、kc、θ2以优化叶轮效率及扬程,参数说明见表2。在鱼类友好型设计方面,Amaral等[8]指出,叶片前缘倾斜和大前缘厚度可以提高叶片撞击存活率。潘强等[11]提出,采用螺旋形叶片前缘可大幅降低撞击速度,提高鱼类受到叶片撞击后的存活率。Van Esch等[6-7]提出的叶片撞击模型表明,鱼类通过性能与叶轮处过流断面面积有关。

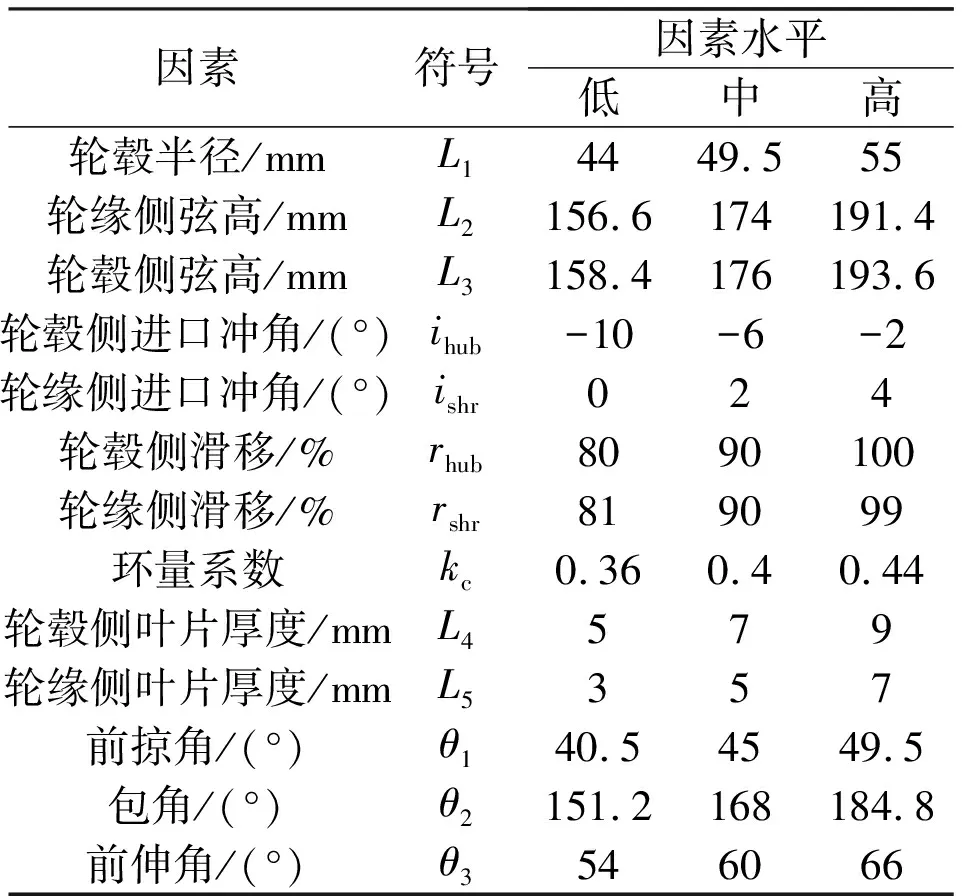
表2 田口设计优化参数表(13因素3水平)

综上,本文选取参数L1、L4、L5、θ1、θ3以优化鱼类通过性能。上述参数在表2中说明,并在图10、11、12中标注,图10为叶轮轴面投影图,图11为叶轮水平面投影图。图12为翼型展开图,其中β1为轮毂侧叶片进口安放角且等于液流角β′1与冲角ihub的和,本优化通过控制冲角大小来调整叶片进口安放角的值。

图10 叶轮轴面投影图

图11 叶轮水平面投影图

图12 贯流泵叶片翼型展开图

2.2 敏感度分析实验

本次优化选择13因素3水平,依据田口设计法得到27组方案,各因素名称、缩写符号及因素水平如表2所示。

利用Minitab软件进行敏感度实验分析,得到其信噪比响应如表3所示,其中排秩越靠前表明其对目标影响越大。为进一步分析上述13个因素与优化目标之间的关系,取3水平中的高、低两水平进行Plackett-Burman筛选实验设计,绘制具有标准化效应的Pareto图,如图13所示,纵坐标为各因素名称,横坐标为频率,图中标有频率参考线,超过参考线的因素称之为显著因素。选取上述两种方法中对各目标影响排序前5的因素,剔除重复因素后发现两种方法选择的因素完全一致,分别为L1、L2、L3、ihub、L4、L5、θ1、θ2、θ3。因此,取这9个因素作为2.3节实验设计的最终因素。

表3 敏感度分析实验信噪比响应排秩

(a)效率

2.3 实验设计

常见的实验设计方法有全因子法、中心复合法、正交实验法、拉丁超立方法等[26]。本次优化的实验设计采用最优拉丁超立方法,抽取125组数据作为样本库。该方法可在设计空间内均匀采样,每个因素都有n个水平,每个因子水平通过执行准则后随机组合且只进行一次组合。相较于其他实验设计方法,该方法可以捕捉到更高阶的效果[27]。

2.4 近似模型

常用的近似模型有响应面法、人工神经网络、Kriging模型、混合近似模型等[28]。本次优化采用Kriging模型来构建近似模型,它具有局部估计的特点,包含回归部分与非参数部分[29],表达式如下

(4)

式中:fj(x)为k个已知的回归函数;βj为回归系数;Z(x)为相关函数。

采用无偏估计模型,估计任意两个z(si)和z(sj)之间的协方差,即

cov[z(si),z(sj)]=σ2r(si,sj)

(5)

式中:si和sj为任意两个样本点;σ2为过程方差;r(si,sj)为空间相关函数。

本次优化通过在样本库内抽取100组数据生成近似模型,以剩余的25组数据来检验模型,采用的Kriging模型参数设置如表4所示。

表4 近似模型参数设置

生成模型后,通过使用决定系数R2与均方根误差σRMSE交叉验证模型准确性,其数值可利用式(6)、(7)计算。一般认为,R2在0.9以上,σRMSE小于0.1,则该模型具有较高准确性[30],本次优化构建的代理模型的R2与σRMSE如表5所示,因此本次构建的代理模型的准确度足以满足本次优化需要。R2表达式如下

表5 代理模型的准确性

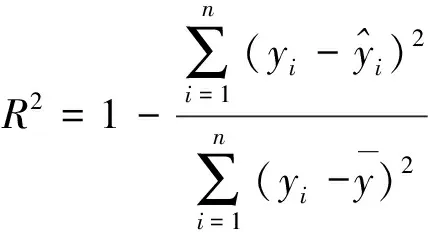
(6)

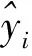
σRMSE表达式如下

(7)

式中:σRMSE为均方根误差;N为样本数;Yi为真实值;f(xi)为预测值。

2.5 优化算法

对于多目标优化问题而言,要求所有子目标均能取得最优值,大多数情况下极难实现。各目标之间的冲突通常难以调和,往往呈现一种此消彼长的状况。Deb等[31]提出一种求解Pareto最优解的带精英策略的快速非支配遗传算法(NSGA-Ⅱ)。该算法使用了快速非支配排序法以减小计算复杂程度,同时引进精英策略使得样本采集范围得以扩展,大部分优秀个体得以保留,而且利用拥挤度的概念,提高同一支配层的种群多样性。为使本次优化的Pareto最优解具有良好的收敛性与鲁棒性,采用该算法进行求解,部分参数设置如表6所示。

表6 优化算法参数设置

在优化过程中,通过不同权重因子配比对水力效率与鱼类存活率组成的目标函数进行了3种方案的算法寻优,其中,扬程作为约束条件参与。该优化问题的目标函数如下

(8)

式中:f1(x)为近似模型中效率的代理函数;f2(x)为近似模型中鱼类存活率的代理函数;a、b为权重因子;H为扬程。

3 结果与讨论

3.1 优化结果

采用NSGA-Ⅱ算法求解灯泡贯流泵的多目标优化问题,经过104次迭代以后,Pareto边界趋于稳定,迭代过程及优化结果如图14所示。方案A、B、C分别为效率最优个体、折中个体、鱼类存活率最优个体,权重因子配比分别见表7。各方案的详细参数及额定工况下定常计算结果如表8所示,方案A、B的效率较初设方案提升了5.2%、4%,方案B、C的鱼类存活率较初设方案提升了21.5%、49.4%。可以看出,优化后的方案在侧重考虑的性能方面均较初设方案有所提升,但也导致其他方面性能一定程度的下降。因此,如何选择真正合适的优化方案仍需工程师结合工程实际需求进一步考量。

表7 各方案权重因子配比

表8 各方案叶片参数对比(Lf=75 mm, Lf/D=1/4)

图14 NSGA-Ⅱ算法迭代求解Pareto前沿

初始方案与3个优化方案的轴面投影图、水平投影图与叶片实体对比图如图15所示。结合表8可以发现,方案B、C的θ3数值较方案A有大幅减少,尽管L2数值也在逐渐减少,但仍然导致叶轮叶片在轴向投影上的长度较初始方案与方案A大幅增加。方案B的θ1、θ2数值较大,因此其在水平投影图的圆周方向上长度也较长。

(a)轴面投影对比

观察3个优化方案中对鱼类存活率影响较大的因素数值可发现,3个方案的L1数值递减,因而导致叶轮过流断面面积逐渐增大,撞击概率减小,θ3也呈递减趋势,而L4、L5的平均值递增,该数值将影响撞击死亡率系数。与此同时,方案B、C的θ1相较方案A 增大,该数值会对叶片前缘撞击速度产生影响。

3.2 水力性能

各方案外特性曲线如图16所示,可以看出,方案A、B在多数工况下的水力效率均较初设方案有明显提升,而方案C的性能曲线与初设方案相比相差较大,其效率曲线更为平缓。

图16 优化前后各方案外特性曲线对比(效率+扬程)

3.2.1 压力分布对比

各方案的叶轮叶片吸力面静压分布如图17所示,初始方案的叶片前缘存在低压区,其中轮毂侧低压范围较大并有向后缘扩散的趋势。叶片前缘流动复杂,过低的压力极易在该处诱发空化现象,导致流场不稳定,效率降低。相比而言,方案A、B采用了相对较小的L4、L5,减小了来流对前缘的撞击,较大的θ3使得叶片前伸程度更小,合理的ihub改善了由于径向流动导致的进口安放角与液流角的不匹配问题,因而在一定程度上减少了低压区面积。其中,方案A的过渡更顺畅平和、梯度明显,更好地遏制住了扩散趋势。但是,更多考虑鱼类通过性能的方案C则表现不佳。当来流受叶片前缘作用径向运动时,趋向于朝叶片吸力面的低压区流动,较小的L1增大了锥形轮毂的锥度,使轮毂侧液流的轴向速度进一步受到抑制。因此,其前缘低压区面积进一步增加,轮毂侧压力分布较为紊乱,并伴随有向后缘及叶片中部扩散的趋势,可能导致必须汽蚀余量降低。

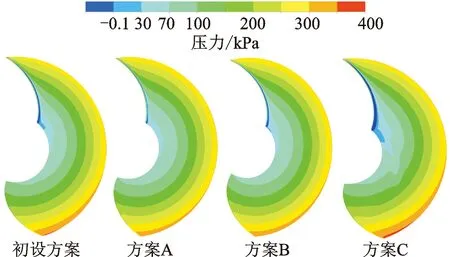
图17 各方案叶轮叶片吸力面压力分布对比

3.2.2 湍动能分布对比

湍动能可表征流体速度脉动的剧烈程度,数值越大,则表明流体流动越不平稳[32],分析该数值的分布情况,有助于进一步了解固体壁面附近的流动损耗[33]。如图18所示,各方案吸力面湍动能较大的区域均集中在轮缘侧,其中靠近前缘处的湍动能最大,即图中红色表示的区域。方案A、B通过优化降低了该区域的湍动能,减少了损耗,而方案C的情况比较糟糕。方案C由于充分考虑鱼类通过性能,因此采用了更小的θ3,其叶片前伸程度更大,导致更加剧烈的径向流动,湍动能因此增加。同时,方案C的L4、L5较其他方案有了大幅度增加,叶片厚度更大,加之叶片前缘靠轮缘侧的相对速度较大,造成该区域极易产生流动分离及旋涡,湍动能也更大。值得关注的是,剧烈的径向流动可能是导致方案C的高湍动能区域有从轮缘侧向轮毂侧扩散的原因之一。除此以外,通过观察图18中虚线框选的部分可发现,初设方案及方案B、C的湍动能在轮毂侧出现了不同程度的突变,而方案A则通过优化极好的规避了这种现象的发生。

图18 各方案叶轮叶片吸力面湍动能分布对比

3.2.3 局部熵产率分布对比

对于水泵而言,因其工作介质的黏性及存在雷诺应力,使得其在运行过程中机械能不可逆地向内能转化,带来不可逆的能量损失[34]。一些研究者通过能量分析聚焦水力机械中的局部损失区域,开展针对性的流动不稳定分析及优化设计,取得了良好的效果。Kock等[35]提出了一种计算局部熵产率的理论,被证明是科学、准确的,也是目前学者们使用的主流方法之一。本文采用这种方法进行各方案的局部熵产率计算。

各方案在展向0.02、0.5、0.98处的熵产率分布如图19所示。以图19(a)初设方案为例,该图左侧为叶轮展向截面,右侧为导叶展向截面,图中红色所示代表该区域的熵产率较高,是高损失区域。通过观察图19(a)可以发现,方案A几乎消除了初设方案中叶轮吸力面的高损失区域,同时通过优化叶轮的方式减少了导叶部分的高损失区域。对于方案B而言,尽管优化后的叶轮吸力面仍存在高损失区域,但其导叶部分的高损失区域较初设方案减少了。对于充分考虑鱼类通过性能的方案C而言,其在叶轮与导叶部分存在大量高损失区域,这必然会导致其水力效率的下降。同时,通过观察图19(b)的导叶末端与图19(c)的叶轮末端均可以发现,方案A、B较初设方案有了一定提升,但方案C的表现则相对较差。

(a)展向0.02

3.3 鱼类损伤评估

鱼类损伤评估是对鱼类通过性能的量化估算与分析,也是对旋转机械鱼类友好型设计效果的检验[36]。本文从撞击概率、撞击死亡率、鱼类存活率方面进一步分析优化后的3种方案,同时引入无量纲数Lf/D,以关联鱼体长度与泵类关键参数,使得相关研究结论更具普适性。

3.3.1 撞击概率

通过计算得到各方案在不同鱼长下的撞击概率,如图20所示。各方案在面对同等鱼长时的撞击概率相差非常小,说明对于不同鱼类友好型设计的叶轮,在撞击概率方面的差异是很小的。结合式(3)可知,撞击概率虽为影响鱼类存活率的因素之一,但并非主要影响因素。

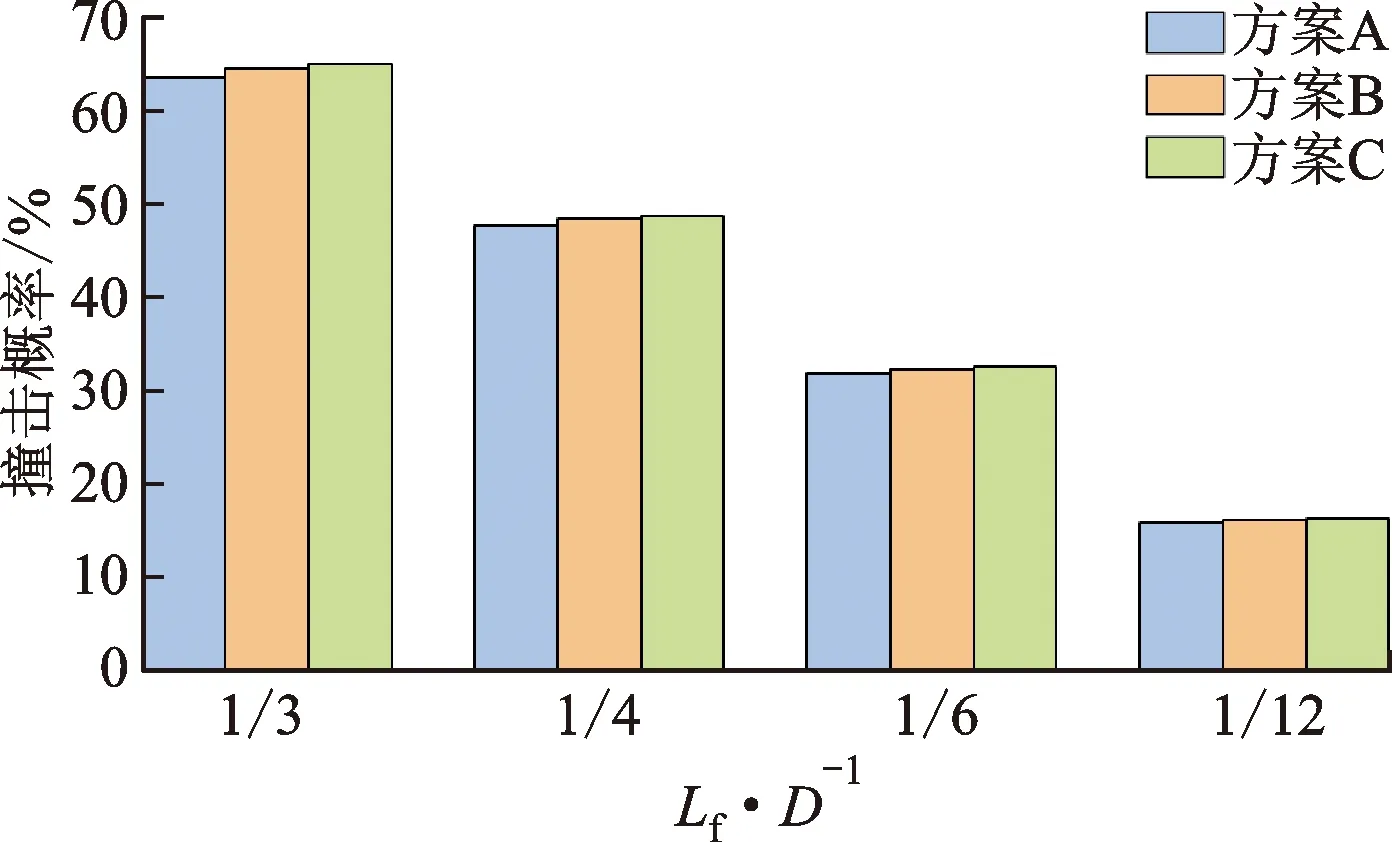
图20 各方案不同鱼长下的撞击概率对比

3.3.2 撞击死亡率

撞击死亡率受损毁率与撞击速度影响,本文将从这两方面分别进行分析。撞击死亡率和撞击速度表达式如下

(9)

(10)

式中:k1为损毁率;d为叶片厚度;v1为撞击速度的圆周分速度;v2为撞击速度的轴面分速度。

表9列出了各方案在不同鱼长下的损毁率k1,该数值越低,则在同等撞击速度下,鱼类撞击死亡率越低。可以看出,方案B、C由于考虑了鱼类通过性能,在同等鱼长条件下,其损毁率均较方案A有所降低,且方案C下降更多。对比不同鱼长条件下的各方案损毁率,可发现鱼长越短损毁率越低,且方案C下降更快。综合以上两点并结合式(9)与表9可得出结论,在损毁率方面,叶片厚度较大的方案C更具优势,且这种优势在低鱼长条件下表现得更为明显。

表9 各方案在不同鱼长下的损毁率对比

各方案叶片前缘的vs、v1、v2如图21所示,可以发现,方案A 的vs较高,对鱼类造成的损伤更大,而方案B、C的vs控制得更好,方案C在轮毂侧表现更好,方案B在轮缘侧更具优势。结合表8与叶片撞击模型进一步对比方案B、C参数可发现,由于方案C的θ3更小,导致其v2更小,而方案B的θ1更大,导致其v1更小。因此,在叶片设计过程中需要注意θ1、θ3的取值。

图21 各方案叶片前缘撞击速度对比(轮毂侧-轮缘侧)

3.3.3 鱼类存活率

各方案在不同鱼长下的鱼类存活率如图22所示,可以观察到,各方案在高鱼长条件下的差异较大,而在低鱼长条件下差异不大且表现均较好。尽管方案C在水力性能方面表现不佳,但其鱼类通过性能方面表现最好,在不同鱼长下的鱼类存活率均保持在80%以上。方案A的鱼类通过性能最差,尤其是在高鱼长条件下表现得更为明显,方案B在优化过程中考虑了鱼类存活率,其鱼类通过性能较方案A有明显提升。