热声发动机中的交变流动换热器特性研究

王海涛,罗靖,张丽敏,孙岩雷,陈远航,常德鹏,陈燕燕,余国瑶,罗二仓

(1.中国科学院理化技术研究所低温工程学重点实验室,100190,北京;2.中国科学院大学,100049,北京)

热声热机也称回热式热机,因具有高效率、高可靠性、长寿命等优势而逐渐受到重视[1-3]。换热器是实现发动机内部工作气体与外界热量交换的核心部件,回热器位于高、低温换热器之间,实现热能与声能的相互转换。高、低温换热器与回热器等部件紧密相连,工质在相邻部件间往复穿梭。如图1所示,在热声发动机的换热器中,绝大部分工质在各交界面的突变截面处往复流动,显著的时变惯性与“进、出口”效应使得热声热机换热器的特性必然与定常流动换热器存在显著不同。

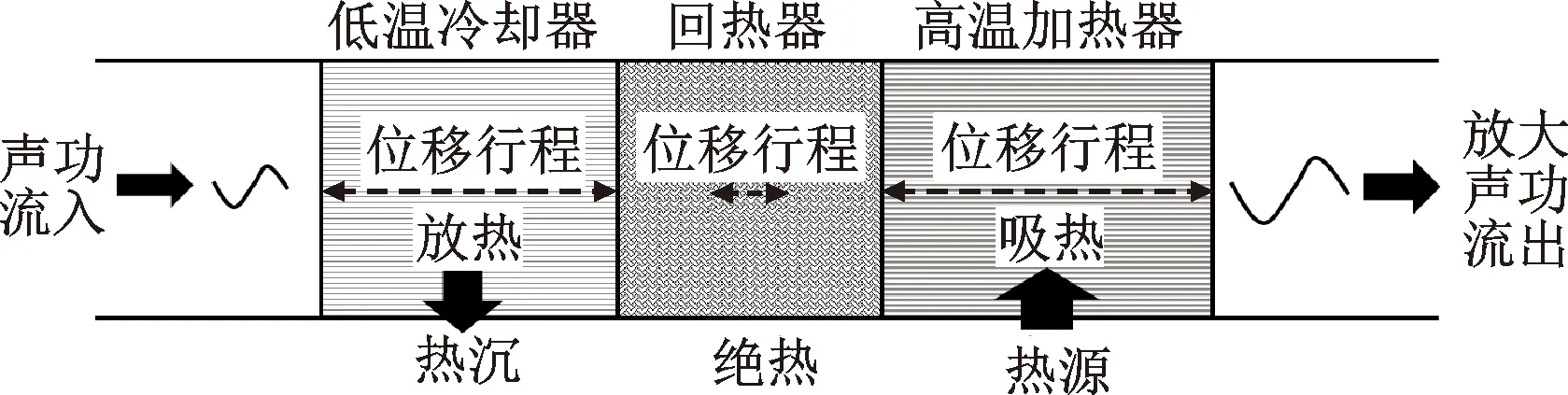
图1 热声发动机核心部件示意图

由于物理过程本身的复杂性与多样性,至今对交变流动及其换热规律的认识与定常流相比仍然相差甚远。理论分析工作主要基于线性或弱非线性热声理论,针对层流充分发展换热器部件进行分析[4-7]。实验与数值分析研究方面,代表性工作主要集中在20世纪80—90年代对斯特林热机的加热器或冷却器的研究[8-12],以及近些年来的二维简单板叠式换热器的仿真与可视化[13-17]、三维瞬态仿真研究[18-20]等。前一阶段的研究主要是借鉴定常流的分析方法,尝试采用阻力系数与换热系数来描述换热器的特征,但所得到的表达式往往相差较大,缺乏普适性,这其中的缘由也鲜少有分析。后一阶段则主要针对简单换热器进行CFD二维与三维模拟以及流场可视化测量,考察不同声场强度下换热器内的瞬态流动、换热分布特征,以及换热器端部的涡流问题等。这种细致分析的结果显示出交变流动换热器与定常流换热器有着显著的不同,首先是热流密度的分布与声场分布及系统其他部件之间的耦合特性非常强;另外,显示出换热器的流动与换热特征主要受进出口效应影响。但是,这类研究未能在流场细节之外总结出规律,且受限于研究的具体热机形式及实验条件(针对的是简单换热器结构、单一声场条件以及低功率密度下的研究),分析结果的系统性、普适性和实用性都显得不足。

随着大功率热声热机发展的需求日益迫切,实际热源耦合的换热器设计越来越成为关键,然而对热机内部交变流动换热器特性的理解尚难以满足发展需求。因此,有必要对热声热机换热器内部的换热和阻力特征展开细致研究,明确换热器内部换热与流动损失特性,系统分析并总结特性规律,有效指导热声热机的工程设计与应用。本文以一台新型10 kW热管耦合自由活塞斯特林发电机的发动机核心单元为分析对象,分别采用回热式热机通用设计准一维软件Sage[21-22]和商用CFD计算软件FLUENT[23],对高、低温换热器内的流动与换热特征进行详细分析。基于拓扑等效模型,对比分析两种计算结果,提出适用于Sage计算的换热器修正模型,提升Sage模型的计算准确性,指导热声热机的工程设计。

1 热管耦合发电机整体设计

1.1 热管耦合自由活塞斯特林发电机结构

热管耦合自由活塞斯特林发电机由实现热声转换的发动机与声电转换的直线电机两部分组成。发动机侧需要实现热管与发动机加热器的结构与热耦合,热管有柱形直热管(亦可大角度弯折)与异形热管两种,如图2所示。柱形直热管更为成熟,与自由活塞斯特林的耦合方式包括热头横截面插入与轴向插入式两种。常规耦合受限于发动机热头在横截面与轴向长度上的过度紧凑,使得热管冷凝段长度与发动机的尺寸适配性较差,只能用于低功率匹配,对于高功率、紧凑型发动机结构的应用存在限制。异形集成式热管加热器能实现发动机与热管之间的高效耦合,发电机功率可达几十千瓦。热管结构与发动机的承压壁集成,异形热管具有显著结构依赖特点,通用性差,结构复杂,工艺要求高,目前尚不成熟。

针对以上问题,本文设计出一种高效轴向直热管自由活塞斯特林发电机,通过降低加热器孔隙率与降低系统工作频率,提高加热器内工质位移幅度,从而有效增长加热器长度,即增长热管冷凝段长度。本文所研究的发电机结构优化设计基于Sage软件完成,如图3所示,为基于热力-电磁设计完成的整机基本结构示意图。直热管插入如图3(b)所示的套筒内,气体在铜块的矩形窄缝中进行往复流动换热,同时为实现热管加热器与发电机的高效耦合,负载发电机部分如图3(a)所示,采用对置电机的形式,实现单侧发电机热耦合的同时减小系统振动。

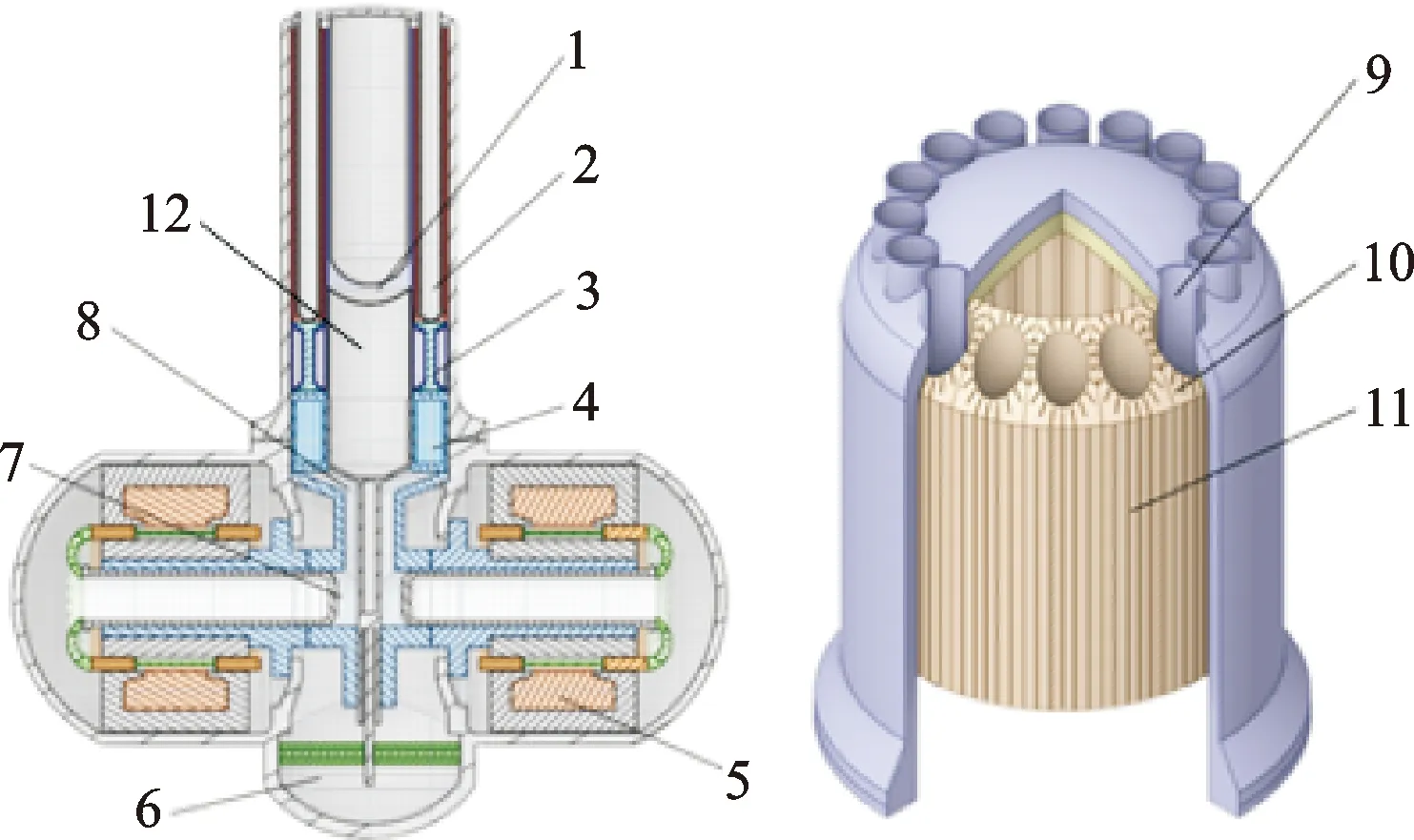
(a)发动机整体结构 (b)热管加热器局部

经设计优化后的换热器结构参数:翅片式高温加热器长度为250 mm,流道宽度为1.3 mm,流道高度为10 mm,翅片平均厚度为7.986 mm,流道数为108,孔隙率为0.046;回热器长度为52 mm,采用丝绵填充,孔隙率为0.897;室温换热器为管壳式,长度为70 mm,管径为2 mm,孔隙率为0.08,流道数为768。

1.2 整机性能参数

热管耦合发电机整机优化后的额定工况性能参数如表1所示。额定设计发电功率为10.77 kW,对应加热器吸热量为30 kW,冷却器排热量约为19 kW。

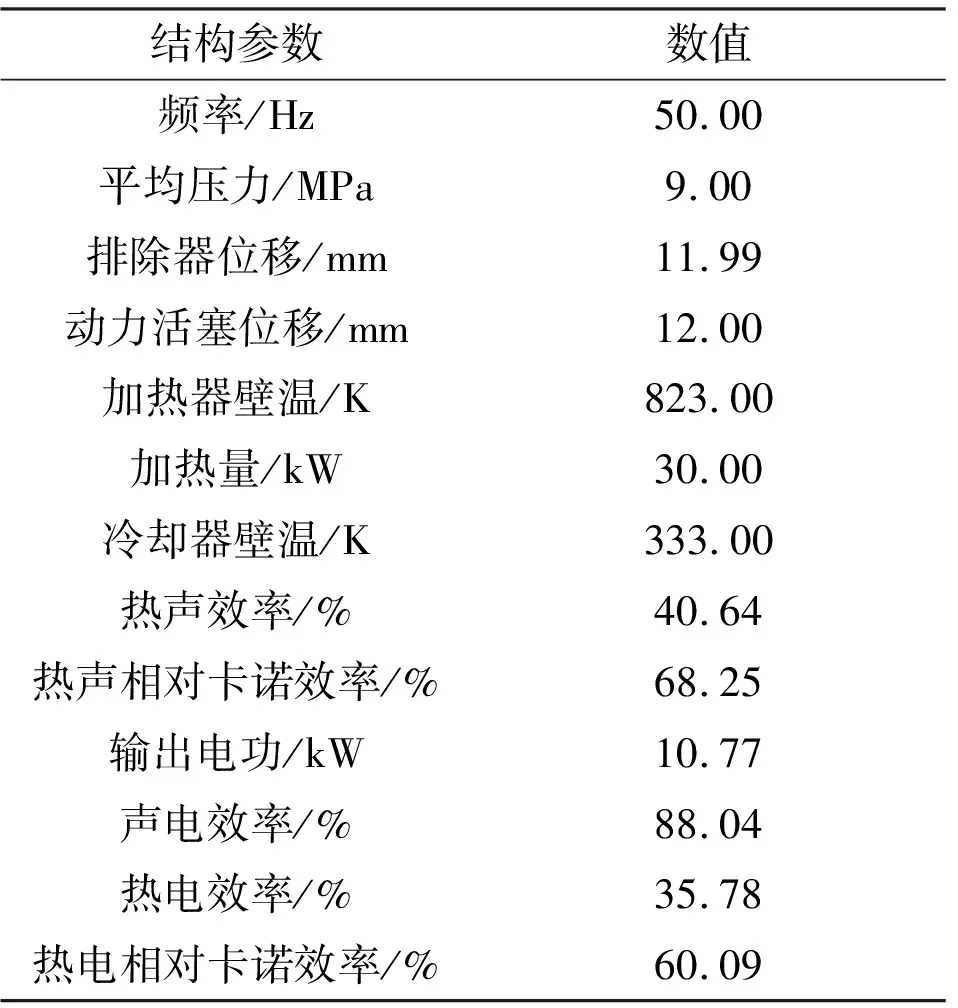
表1 热管耦合自由活塞斯特林发电机性能参数

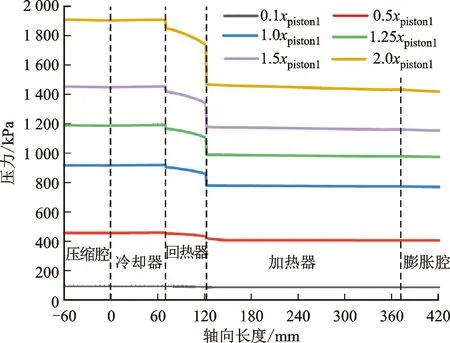
发动机侧冷却器、回热器与加热器核心段的压力、体积流率波动幅值分布如图4(a)所示,声功、声阻抗相位分布如图4(b)所示。为适应热管冷凝段长度,加热器长度为250 mm,可见加热器内明显的压力幅值下降与声功降低,即加长的换热器明显增加了声功损失。

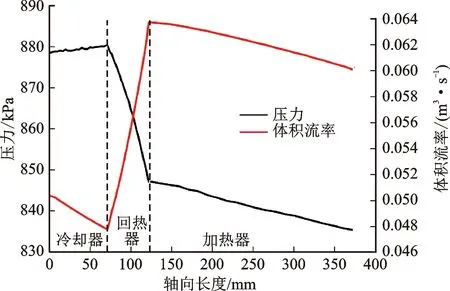
(a)发动机内压力波动与体积流率分布

基于以上热管耦合发电机结构与发动机核心部件额定工况,本文以冷却器、回热器与加热器组成的核心单元为研究对象,耦合热声转换,重点分析加热器与冷却器内的流动与换热特性。

2 换热器计算模型

2.1 换热器拓扑等效

为实现对换热器内流动与换热特征的系统分析,同时简化计算过程,将三维流体计算区域通过拓扑等效简化为二维平面结构。加热器与冷却器均为窄缝结构,相邻的部件为回热器与空腔(加热器侧连接膨胀腔,冷却器侧连接压缩腔),回热器为多孔介质结构,具有显著的均匀化流动效果。因此,回热器与冷却器的拓扑对应性即可解耦,即将加热器与冷却器窄缝简化为二维结构时,与回热器的结构匹配只需要满足界面上的孔隙率对应即可。由于换热器孔隙率相对于回热器与空腔足够小,因此忽略换热器窄缝三维分布对回热器与空腔内射流与二维射流的差异。以狭长窄缝二维等效为基础,以孔隙率最小的加热器一条完整窄缝为最小计算单元,以窄缝宽度为基准。冷却器原设计为管束,二维近似通过水力直径、换热面积及孔隙率相近原则进行等效,等效后的窄缝数量取相对加热器邻近整数,适当调整水力直径以匹配相对孔隙率,回热器宽度与空腔宽度以相对换热器孔隙率确定,加热器、回热器、冷却器的长度保持不变,空腔长度则以相对容积确定。从而将三维结构等效为二维平面结构。压缩腔与膨胀腔容积根据CFD动活塞运动要求进行容积扩展,以压缩腔与冷却器界面、膨胀腔与加热器界面上的压力、体积流率与整机完全相同为原则,将计算边界外延。

图5为按照拓扑等效原则获得的自由活塞斯特林发电机二维模型,结构参数如表2所示。基于该二维模型,可同时采用sage与CFD进行仿真计算,sage一维模型计算结果即可以与原整机设计计算结果进行对比校验,以检验拓扑简化过程的合理性,同时也可为CFD局部仿真提供边界条件。基于CFD仿真对换热器时变换热特征进行详细分析,并与sage一维模型计算结果进行对比,考察sage一维模型计算的有效性。

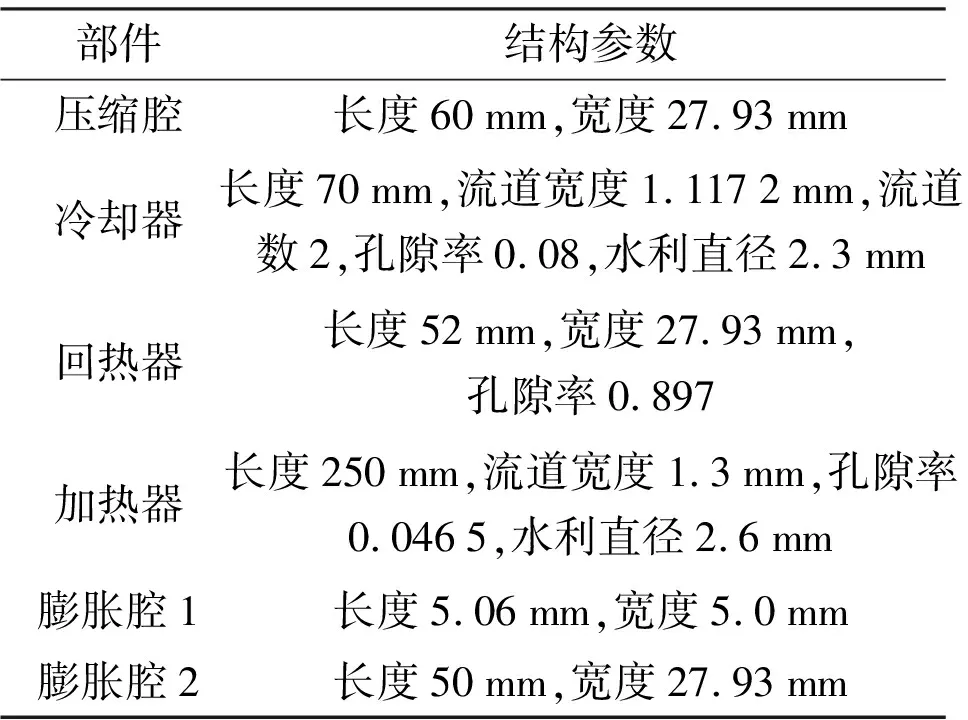
表2 等效换热核心单元结构参数

图5 发动机核心单元拓扑等效模型

图5所示计算模型中,高温加热器的壁面温度为823 K,低温冷却器的壁面温度为333 K,其它壁面边界设置均为绝热。轴向计算边界为避免开口边界带来的入流焓流不确定性,采用双活塞边界进行计算。活塞边界即设定往复振荡虚拟活塞边界面,模拟活塞对热声核心单元的往复压缩、膨胀效应,能量从边界上以时均声功形式进出系统,活塞边界可设置绝热,无不确定性能量,因此对于系统内部的能量分布分析精度更高。Sage一维模型可采用虚拟活塞边界进行计算;CFD仿真中,两端虚拟活塞边界则必须采用动网格,为保证活塞相对平衡位置不变,还需要进行模拟充气与活塞同步的初始过程模拟。活塞同步后,即可加载压缩活塞与膨胀活塞运动的速度控制,活塞速度随时间的变化函数如下

upiston(t)=ωxpiston1cos(ωt+θpiston)

(1)

式中:xpiston1、θpiston分别表示活塞面的位移幅值与相位;ω是角频率。

2.2 Sage一维模型

Sage是由美国Gedeon等于1995年根据MS-DOS编写开发的一款商业计算软件,主要是针对回热式热机的通用设计计算软件。其采用图形化界面将与实际物理组件相对应的气体流动、传热和其他建模细节封装在一些特定的模型组件中,用户通过将封装好的组件按照特定的需求进行相互连接,即可对复杂的回热式热机系统建立仿真模型,利用质量、动量和能量守恒方程、本构方程将各部件的参数进行有机耦合,最终实现整机的求解与多参数协同优化。图6给出图5所对应的Sage一维计算模型。

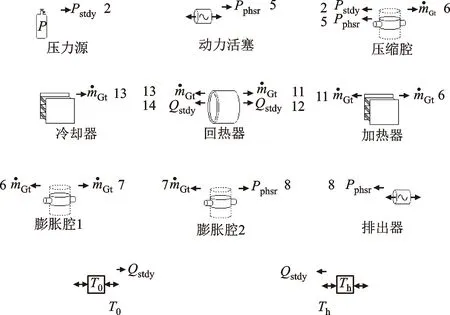
ρstdy—系统载荷;Pphsr—体积位移;mGt—进出口的质量流;Qstdy—线性热源;T0—低温热源;Th—高温热源。

回热器模型选择软件内嵌的丝绵多孔介质模型,其阻力的本构方程如下

f=a1/Re+a2Rea3

(2)

式中:a1=25.7α+79.8;a2=0.146α+3.76;a3=-0.002 83α-0.074 8;α=ε/(1-ε);ε为孔隙率。

换热特性的本构方程如下

Nu=1+b1Peb2

(3)

式中:b1=0.186α;b2=0.55;Pe为贝克来数,即雷诺数Re与普朗特数Pr的乘积。

等效模型中的换热器均为平板模型,采用软件内嵌的板式换热器模型,基于线性热声理论平板模型获得板式换热器模型的阻力与换热特征层流,湍流则借用湍流平板稳态流动特性,本构方程如下

f=0.11(ε/dh+68/Re)0.25

(4)

Nu=0.035Re0.75Pr0.33

(5)

式中:dh为丝绵等效水力直径。

Sage一维模型中可通过设置额外的阻力系数,对模块进行整体阻力修正,阻力修正通过定义以下压力梯度表达式中的K实现。即计算模块的压降由模块特征阻力系数f与附加可用户自定义的阻力系数K决定。

在流动方向上的压降表达式如下

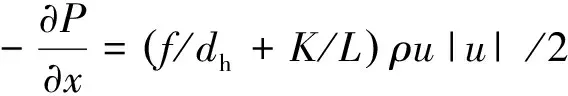
(6)

式中:L为模型长度;ρu|u|/2为流体动能。

2.3 CFD模型

CFD仿真使用ANSYS FLUENT 2021 R1版本。采用活塞边界动网格进行瞬态计算,发动机内氦气的交变流动计算属于小马赫数可压缩流动。将氦气设置为理想气体,采用基于压力法的求解器计算,选用PISO 算法,压力使用PRESTO!离散格式,其他均采用二阶迎风离散格式,时间离散采用二阶时间差分。换热器内流速较高,以幅值雷诺数作为判断基准,加热器雷诺数幅值变化范围在3 000以上,明显高于2 300,因此可采用k-ε湍流模型。模型中计入氦气物性随温度的变化,物性公式列于表3。回热器采用热平衡多孔介质模型,只考虑回热器内流阻模型。阻力系数根据Sage模型中所用的阻力系数公式,通过局部拟合转换为黏性阻力系数与惯性阻力系数表征的阻力特性,获得FLUENT中多孔介质模型设置参数1/K(黏性阻力系数)与C2(惯性阻力系数)。

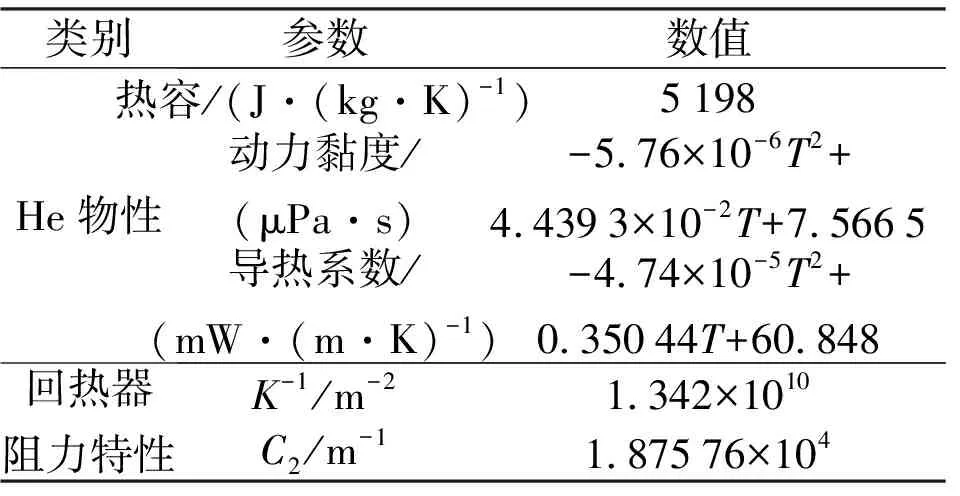
表3 氦气物性参数

2.4 CFD二维模型网格与时间尺度无关性检验

基于额定工况,进行加密网格与时间尺度的计算,同时对压力、体积流率、温度、声功、换热量的波动与时均值进行监测,波动量幅值、相位及时均量均通过FFT分析获得。图7与图8给出了典型参数的影响。其中网格尺度影响相对较小,网格量大于19 800后,对计算结果影响可忽略,因此后续计算网格均采用19 800这套网格模型。

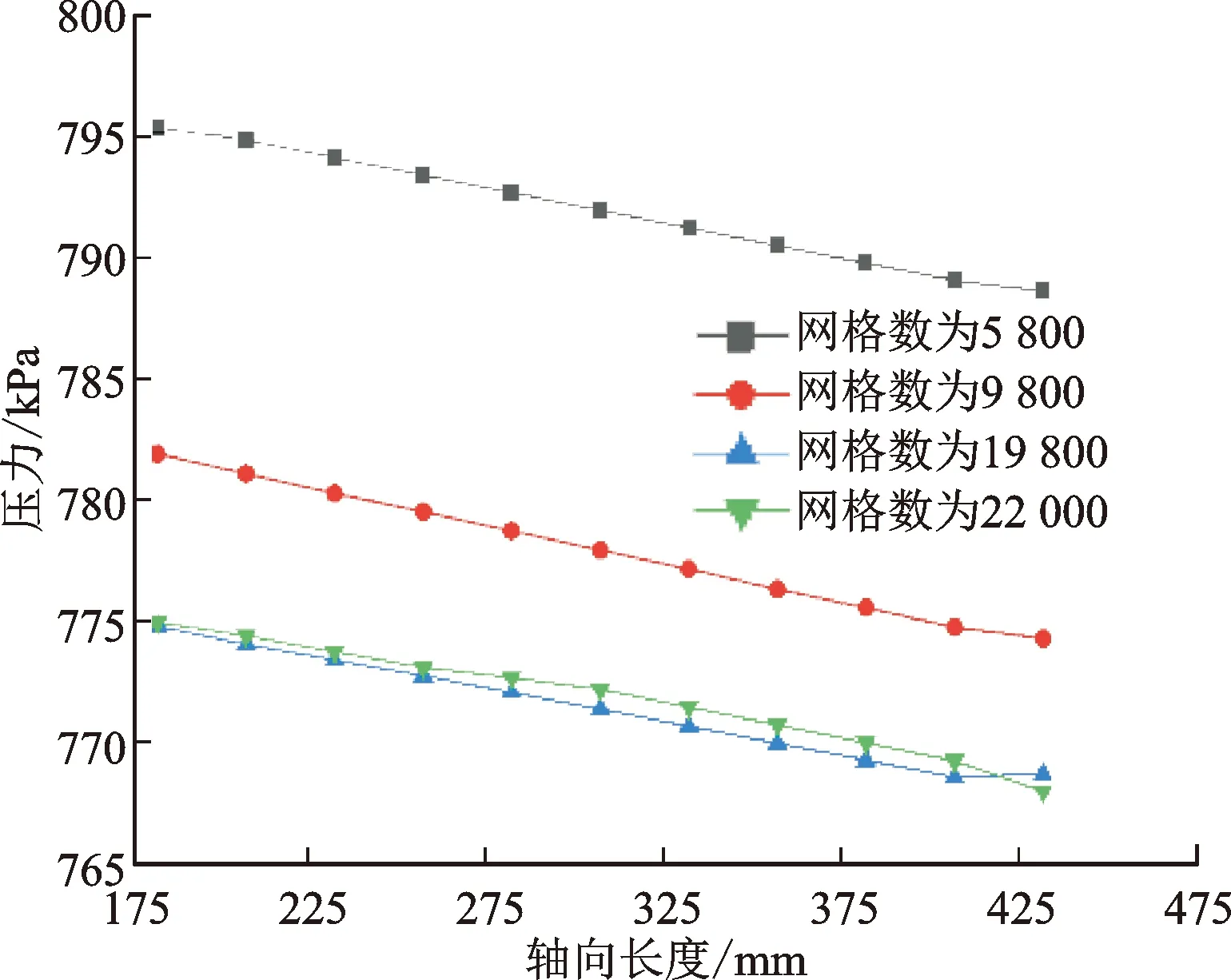
图7 压力波动幅度延程分布随网格数的变化

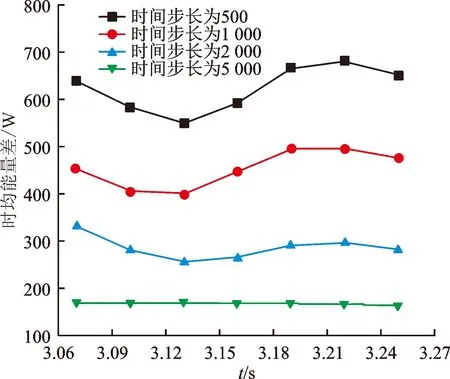
图8 不同时间步长下时均能量守恒性随计算时间的变化

时间尺度对波动参数幅度的影响较小,但是对时均能量的影响较大。由于计算区域为封闭系统,活塞边界的时均声功差异应该等于高、低温换热器的时均换热量差异,但CFD二维模型的时均能量计算发现存在明显的能量不平衡,且该能量不平衡性直接与时间尺度相关。如图8中黑色线代表的每周期计算500个点时,系统有600 W左右的不平衡;每周期计算达到5 000个点时,系统能量不平衡降低到170 W左右。继续减小时间步长,会导致计算量过大,相较于10 kW量级的系统典型时均能流,计算误差可接受,本文选择一个周期计算5 000步。对小时间步长的要求意味着热声系统中时均能量的准确求解较为困难,这主要是因为能量的主要特征为波动量,而时均值为多参数耦合值,相较于波动量为高阶小量,且与参数间的相位关系直接相关,因而计算精度对时间尺度要求非常高。

2.5 额定工况Sage模型与CFD模型计算对比

表4给出了基于图5的Sage模型与CFD模型计算结果对比。其中:Pcomp表示压缩腔入口压力一阶幅值;Pexp1表示膨胀腔1入口压力一阶幅值;PVchxout表示冷却器出口截面时均声功;PVhhxin表示加热器入口截面时均声功;Qchx表示冷却器壁面时均换热量;Qhhx表示加热器壁面时均换热量。两种模型计算均采用相同活塞边界,因此压缩腔与膨胀腔活塞界面处的体积流率完全相同。二者计算的时均能量相当,差异在10%附近,但压力差异相对较大,即内部阻力特性差异较大。

1、20世纪50年代初的探索期是筝乐演奏技术发展的一个分水岭，打破了“右手演奏，左手和声”的观念。这个时期的代表作《庆丰年》。

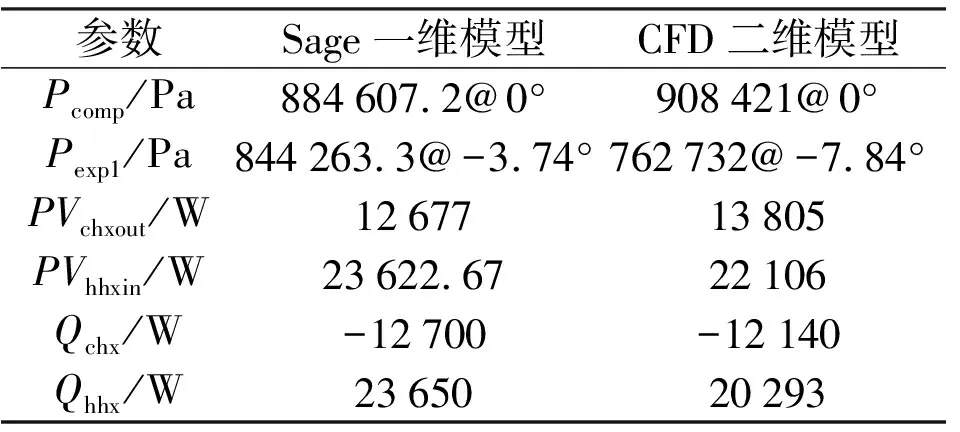
表4 两种模型相同截面计算参数的对比

3 换热器特性分析

为详细分析发动机换热器的换热特性,基于固定结构参数与额定工况,保持其他参数不变,进行不同位移幅度与不同声场相位下的换热器内流动与换热特性分析。其中位移幅值的变化是通过等比例改变活塞速度来实现的,从额定工况的0.1倍变化到2倍,改变位移幅度时,计算区域内的声场相位分布变化非常小。声场相位的变化通过保持额定工况位移幅度不变、改变两个活塞之间的相位差(在0～2π范围内变化)实现。

3.1 换热器内换热分布特性

如图9所示的额定工况下换热分布对比可知,CFD二维模型与Sage一维模型的计算对时均温差与时均热流密度qw分布的捕捉基本相似,数值相近,说明Sage一维模型可以合理地获得换热器内时均换热分布与集中特征。但是,与CFD二维模型计算结果仍然存在明显差异,该差异与温度场的局部二维特性有关,也与流阻损失产生的场能量分布差异有关。计算声场下,换热器表现为靠近回热器一侧换热更为显著,由于为等壁温条件,因此对应的时均温差也更大。

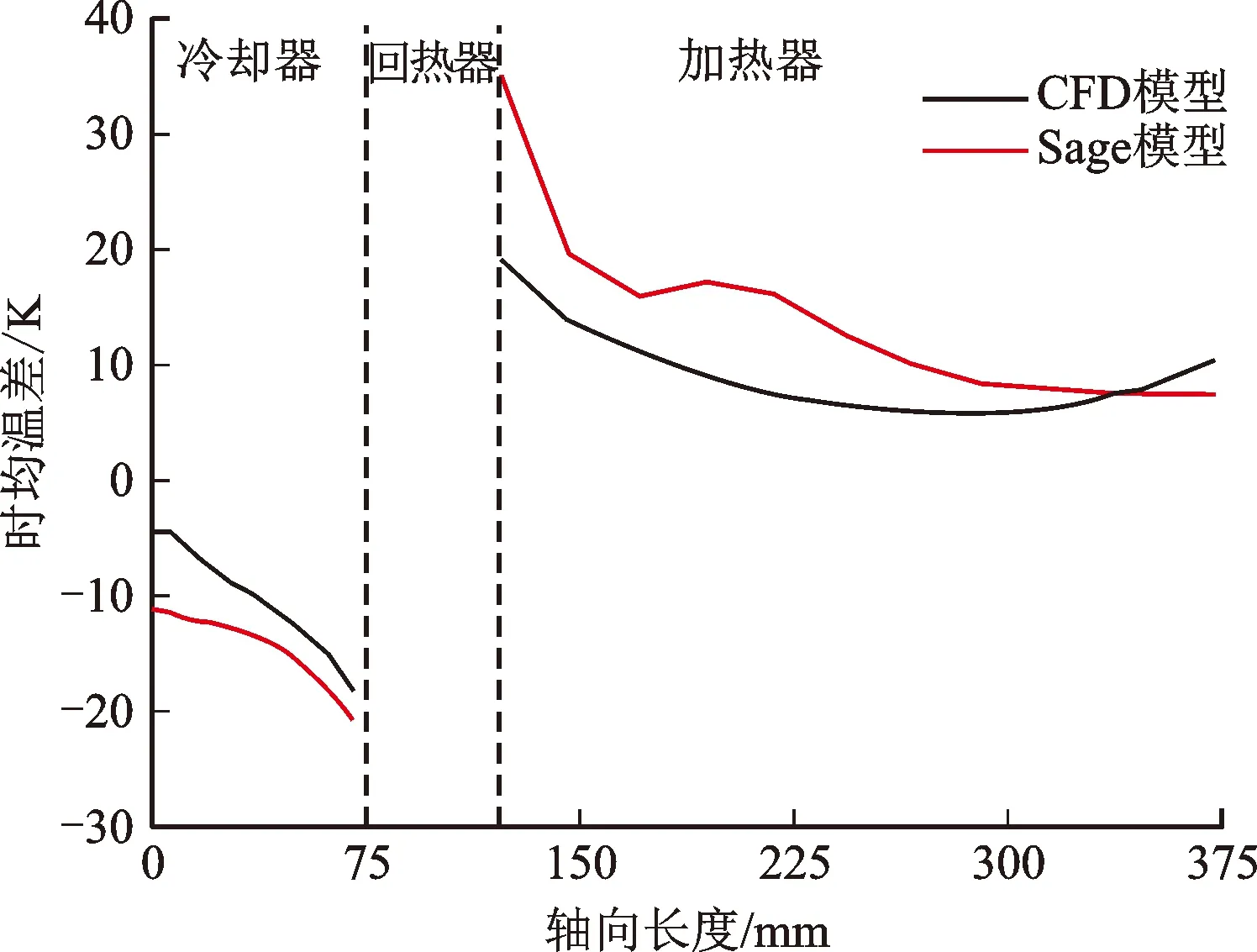
(a)额定工况下换热器内时均温差分布

图10中不同位移幅度下的时均热流密度分布变化表明,随着换热器内位移幅度低于额定工况,换热器内出现无效换热区间(即时间换热为0),超过额定工况后,换热器换热强度分布出现近等比例抬升。Sage一维模型计算与CFD二维模型计算结果结论一致,说明换热器有效长度必须与其内部工质位移幅度相匹配,位移过小,换热器有效换热区域变小,印证了热声系统中的换热器进、出口效应本质与本征紧凑性特征。

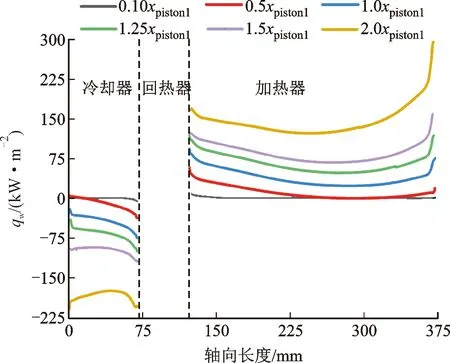
图10 不同位移幅度下时均热流密度分布的CFD二维模型计算结果

图11将时均热流密度与时均气固温差代入努塞特数计算式,获得时均等效Nu(Nu0),冷却器中的Nu0显著高于加热器,且延程分布特性更为显著,对速度也更为敏感。这进一步说明了热声发动机中换热器换热特征具有显著的局部特征。

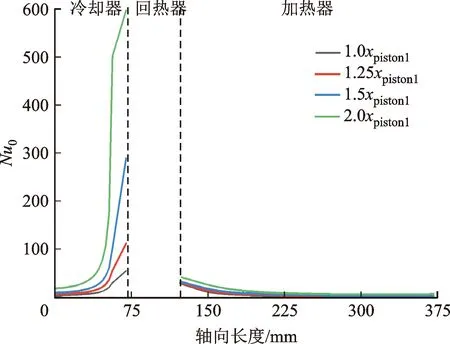
图11 不同位移幅度下Nu0的CFD二维模型计算结果

鉴于Sage一维模型能较好地捕捉换热器内的换热特征,且计算速度显著快于CFD二维模型,因此以下采用Sage一维模型计算不同声场相位时的换热器内换热特性。如图12所示,调节计算边界上的活塞相位差(Δθ),得到的各工况下声场相位分布图。图13给出相应的时均声功分布情况,可见核心单元内的能流分布发生了显著变化。

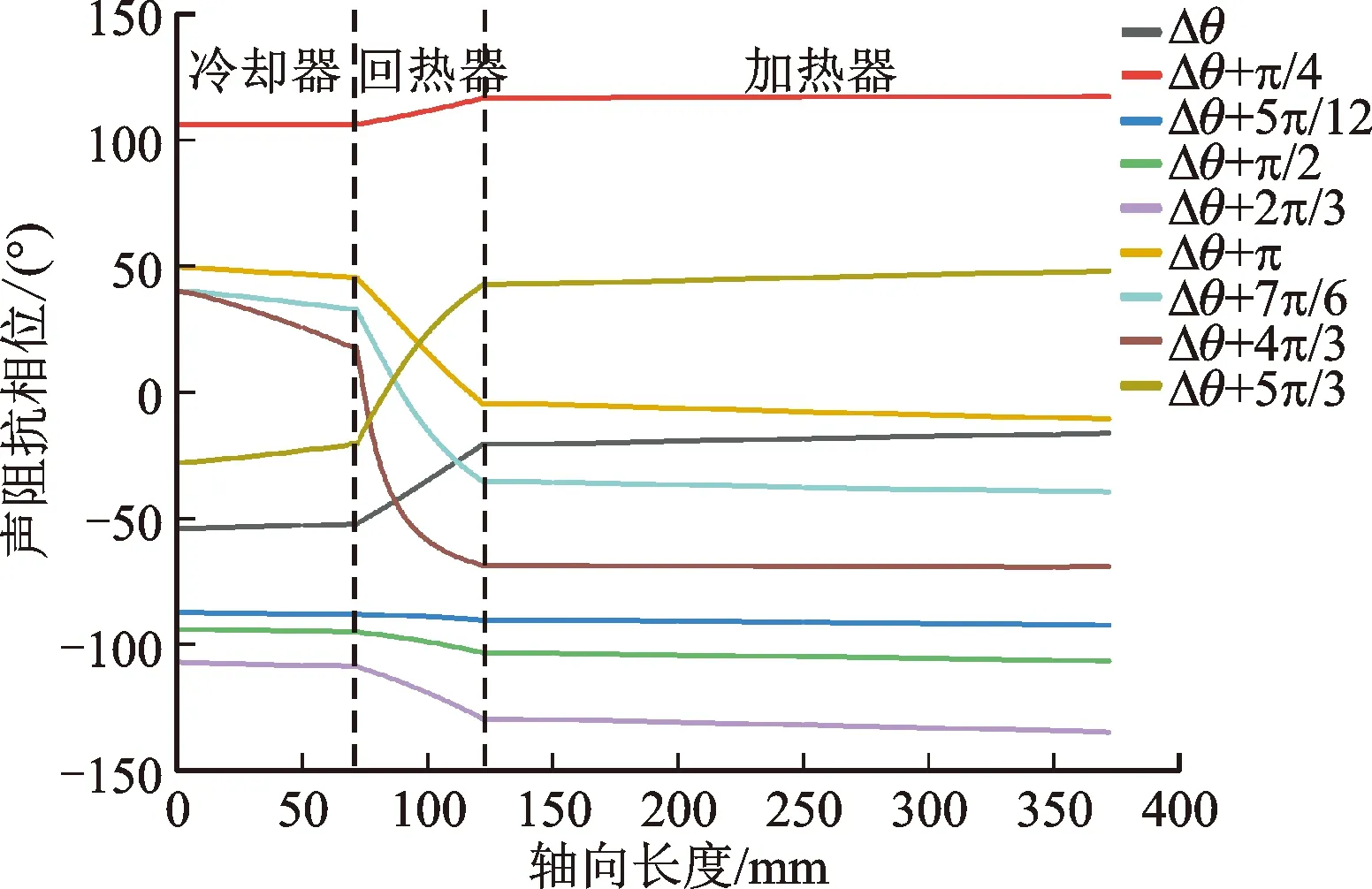
图12 不同边界活塞相位差下的声阻抗角分布

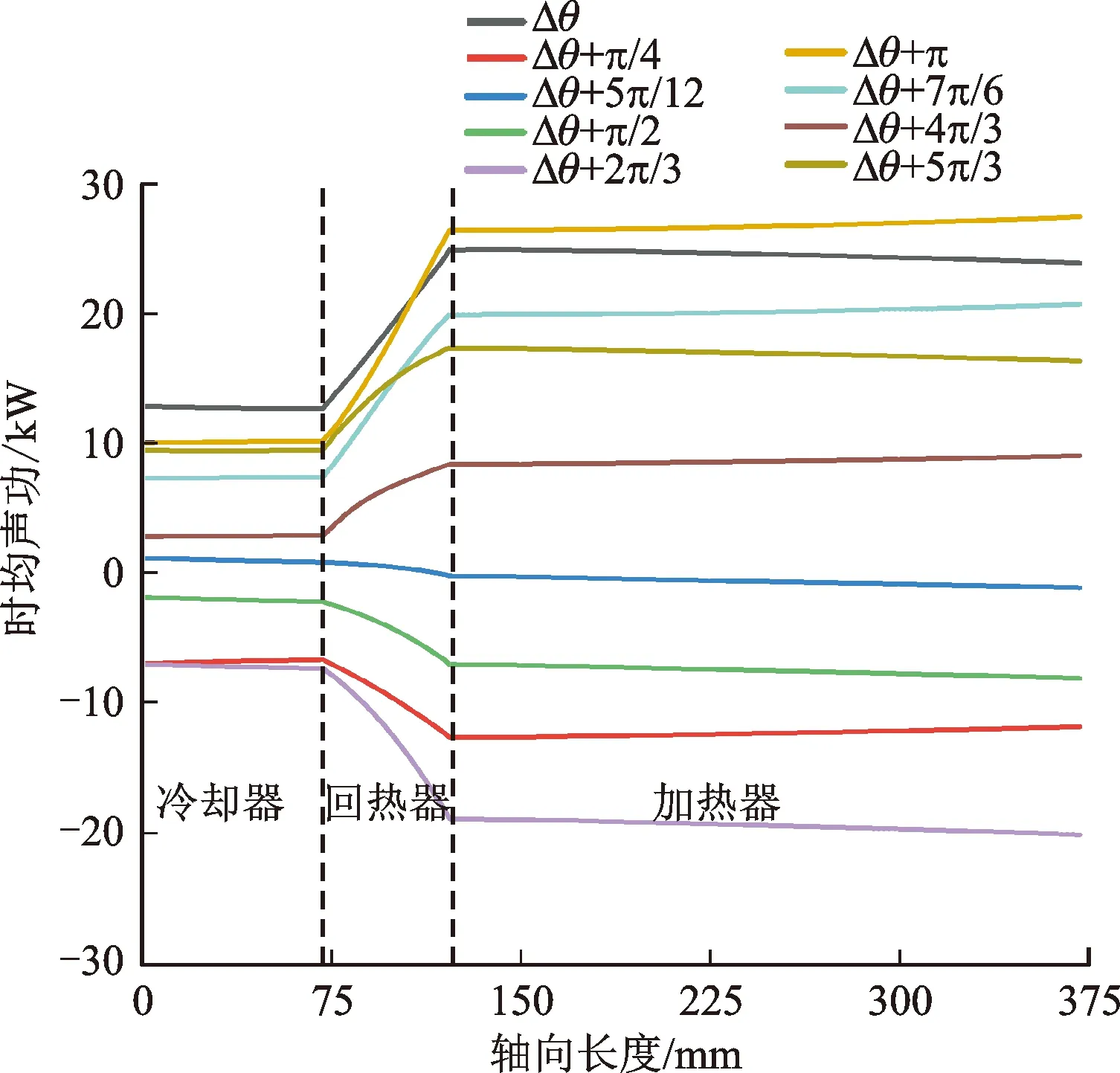
图13 不同边界活塞相位差下的时均声功分布

由图14可知,虽然加热器与冷却器外壁面温度保持不变,即加热器外壁面为823 K,冷却器外壁面为333 K,但声场的变化不仅改变了热流密度分布特性,还决定了换热器是吸热还是放热。因此,热声系统中的换热器换热特性是声场能流驱动的,由时均焓流决定时均换热,而不是温差驱动换热。时均温差是时均能流变化产生时均换热的结果而不是换热的驱动力,这与稳态流动完全不同。

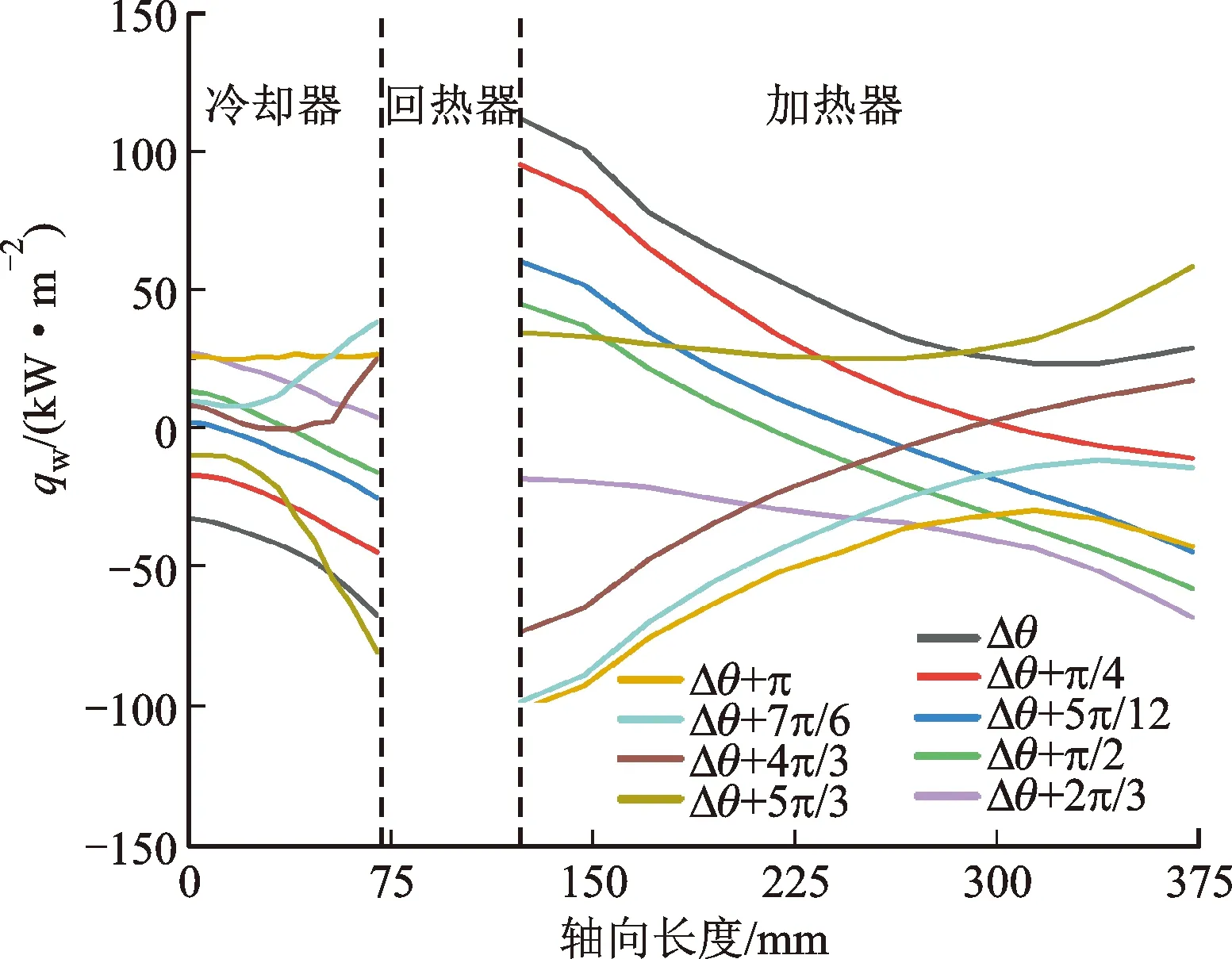
图14 不同边界活塞相位差下的时均热流密度分布

3.2 阻力特性分析

图15给出了额定工况下冷却器、回热器、加热器中压力、体积流率、声阻抗相位角以及时均声功的分布对比。其中最大的差异是压力波动在回热器与换热器的交界面上的压力差异。这是因为Sage作为一维模型无法直接获得复杂流动变化带来的局部损失,且已有换热器模块不能针对部件间的相对结构特征进行自动局部阻力调整,而是需要人为设定相关损失。CFD二维模型仿真可以获得突变截面流场特性的变化,包括射流的影响。从计算结果可以看出,由于加热器孔隙率非常小,在回热器与加热器界面上产生了显著的一阶波动压力损失,时均能量也可看到明显的声功损失。换热器与两侧腔体的连接处损失则相对小得多。这是因为,加热器的高速射流在回热器这一高阻力部件中产生的损失要比射流在空腔中显著得多。这是换热器计算模型中Sage一维模型与CFD二维模型的最大差异来源。

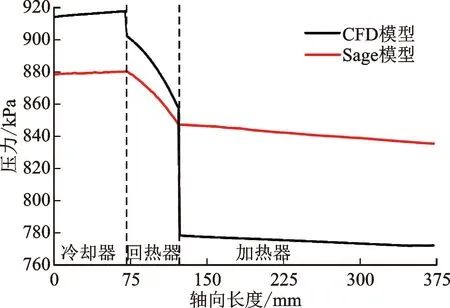
(a)压力

(a)压力

3.3 Sage模型阻力修正

基于CFD模型计算结果,可对换热器与回热器的突变界面处的流阻损失进行特征拟合,反代入Sage模型计算模型进行修正,将修正结果再次与CFD模型计算结果进行对比,即可判断修正模型的适用性。另一方面,基于稳态突变界面局部损失系数与Swift计算方法亦可对突变界面特性进行修正。以下将针对这两类方法进行对比验证。

由Swift方法对热声系统中喷射泵相关理论分析[24]可知,气体往复穿梭变截面时,半个周期经历流道扩张,半个周期经历流道收缩,变截面处的局部阻力系数K应具有时间依赖性,即为时间的函数,因此

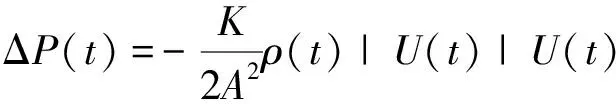
(7)

使用正弦速度

U(t)=|U1|sinωt

(8)

将式(8)代入式(7),可求得平均压降为

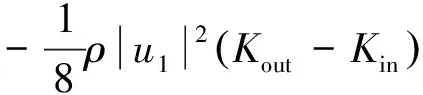
(9)

则其微分形式为

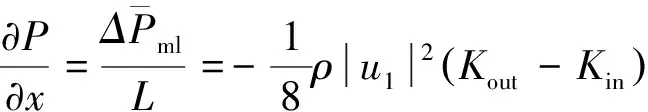
(10)

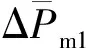
根据稳态流动中面积比与管道截面突变局部阻力系数表[25],计算模型面积比,即可获得交变流动界面等效阻力系数值。

根据CFD模型计算所得压力波动分布进行等效阻力系数修正尝试了两种方法:一种是针对波动压力幅值与速度幅值进行修正;另一种是针对波动压力与速度的有效值进行修正。其中波动压力幅值修正通过下式计算出CFD二维模型的波动幅值压降与速度幅值之间的关系,再计算出总阻力系数Ktotal

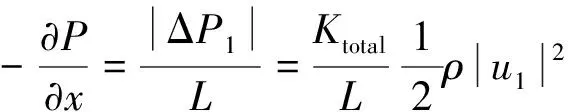
(11)

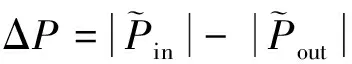
(12)

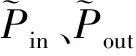
对于有效值计算法则,根据下式计算CFD二维模型的换热器压力与速度瞬时值,再计算出总阻力系数Ktotal

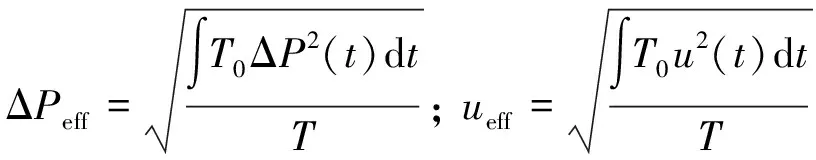
(13)

通过以上方法,针对冷却器与加热器在不同速度幅值下的总阻力系数进行计算。Swift计算方法获得的阻力系数与速度无关,CFD模型数据处理获得两种阻力系数是速度的函数。将以上3种修正方法进行对比发现,采用有效压降法获得的修正最为有效。基于有效压力修正方法使得Sage模型波动压降与声功损耗均高于CFD模型计算结果,但差异存在比例关系。因此,基于有效压力的修正方法需再引入一个阻力系数修正因子

φ≈0.7

(14)

冷却器修正后的有效总阻力系数如下

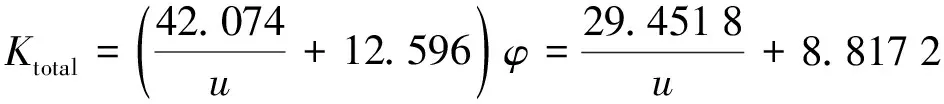
(15)

加热器修正后的有效总阻力系数如下

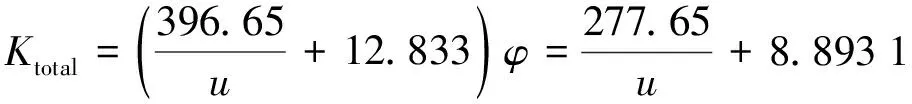
(16)

以CFD模型计算为基准,各种修正方法所得加热器与冷却器的波动压降以及时均声功的误差见图17。

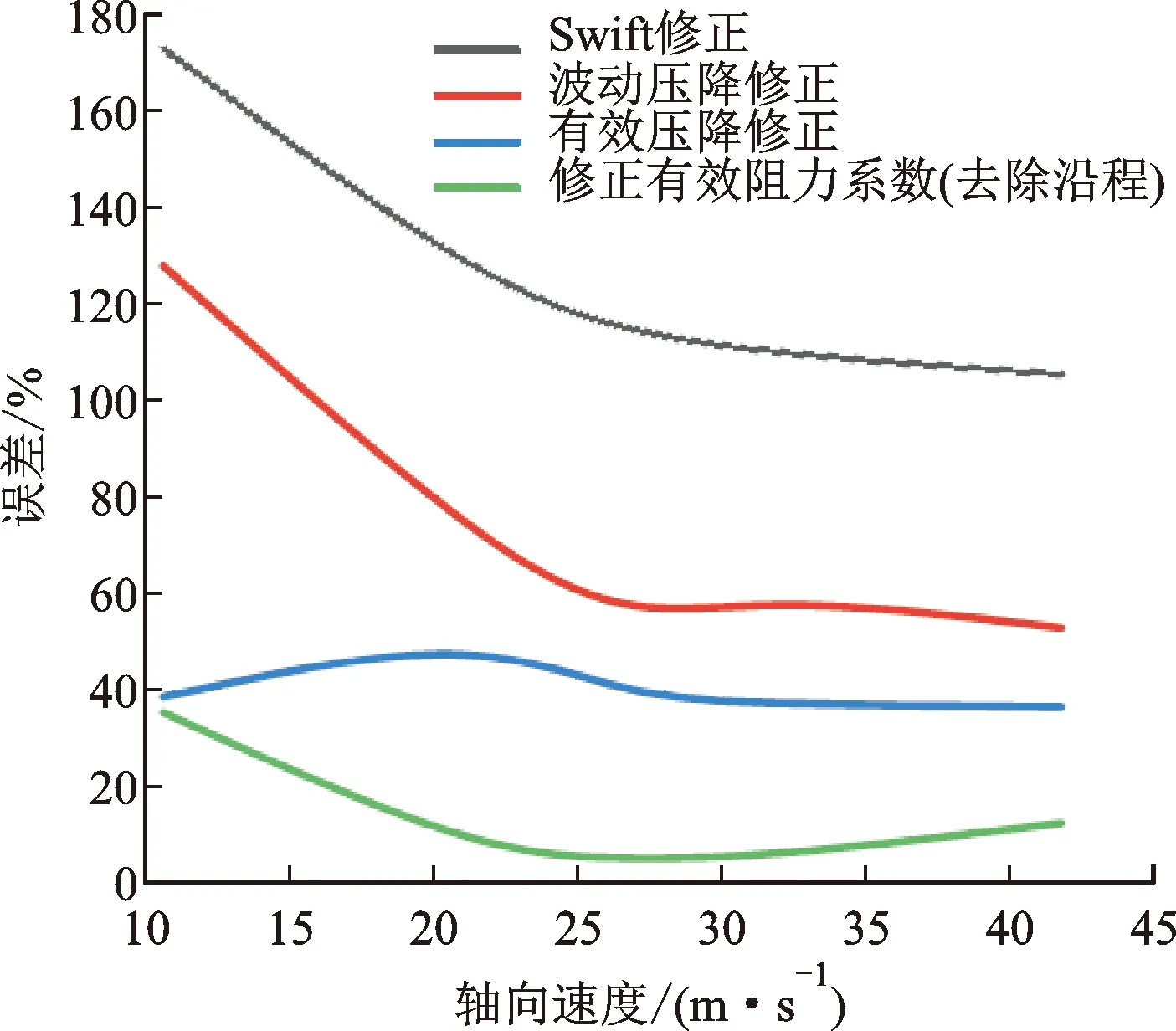
(a)冷却器波动压降误差

由图17可知,经修正因子修正后的有效阻力系数可使Sage一维模型与CFD二维模型计算的换热器两端压差计算差异缩小到20%以内,即Sage一维模型的阻力特性的精度有所提高。换热器声功损失修正精度长加热器比短冷却器明显差,这是因为长加热器的分布特性更难用端部集总压差简单修正得到。如表5所示,整体性能对比表明,Sage一维模型修正后的结果明显向CFD二维模型计算结果靠近。证明通过有效压降与有效速度获得的总阻力系数可用于修正Sage一维模型的阻力特性,可有效提高工程设计精度。

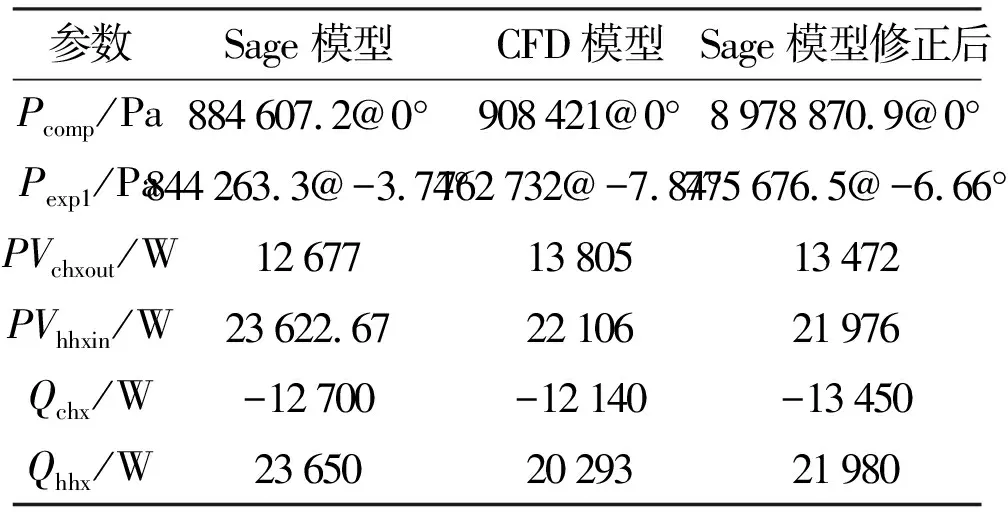
表5 修正前后Sage模型与CFD模型参数对比

基于以上分析,可以建立一套提升实际复杂结构发动机的分析效率与精度的方法。首先利用CFD仿真对真实换热器与回热器组成的核心单元结构进行给定声场下的流动阻力特性分析,由于流阻分析的计算时间稳定较快,可以不需要等待系统热容与时均换热稳定即可进行分析,因而即使对于复杂三维模型的分析计算同样具有工程可行性。所得到的换热器阻力特征可用于修正Sage一维模型中的对应阻力系数。Sage一维模型中换热特性的计算已经可以较为准确地捕捉换热分布与集中特性,因而无需依赖三维CFD仿真模型的热稳定计算。时均换热特性的CFD计算由于对时间尺度的高要求,以及较大系统热容稳定时间尺度之间存在的显著矛盾,使得完全依赖三维CFD仿真进行换热器完整特性分析的计算时间过长而难具工程指导意义。

4 结 论

本文基于10 kW热管耦合斯特林发电机整机设计,进行发动机核心部件的拓扑等效,分别采用Sage一维模型与CFD二维模型两种计算方法,对核心单元的换热与阻力特性进行模拟研究,通过比较两种模型的计算结果,得出以下结论。

(1)对换热器内的局部换热特征以及集总换热特征计算结果对比,Sage一维模型与CFD二维模型具有相近结果,Sage一维模型的分析结果具有工程指导意义。换热器换热特性主要由声场驱动,这可能是换热器换热特征分析中,对本构方程的准确性要求相对较低的原因。

(2)对换热器内阻力特性的计算结果对比表明,Sage一维模型与CFD二维模型计算结果相差较大,换热器射流导致的回热器界面显著损失是产生这一差异的主要原因。因此,为提高Sage一维计算结果的精度,需对利用CFD对实际换热器与回热器界面流阻进行仿真计算,提取阻力特性后在Sage一维模型中进行修正,即可较好地提高Sage一维模型对实际系统的预测准确度。

(3)进一步明确了热声热机换热器特性的显著空间分布特征以及工况依赖特征,这些特征在热声换热器中具有相似性和普遍性。但是,对于特征的量化又因其空间与工况敏感性而难以像稳态流动那样获得通用的本构方程,因而热声热机换热器需要针对具体设计进行特性分析。