2023年高考“解析几何”复习指导

2023-06-15周威童继稀邓捷敏曾文乐张妮

中学数学杂志(高中版) 2023年3期

周威童继稀邓捷敏曾文乐张妮

【摘要】2023年的高考备考要围绕解析几何研究的两个问题——根据条件求曲线的方程、根据曲线方程研究性质来把握备考方向、备考常规及转向；在备考实践中，要把握“题”的分类与导向作用，选出具有代表性的、方向性的试题进行深入分析解析几何的本质、基本思想与方法；同时，不同题型的解题教学要体现“从关注知识”到“关注人”的转变.

【关键词】素养立意;解析几何;题型;实践

回顾2022年解析几何专题考查内容，依然表现在突出主干知识，重视解析几何的本质、基本思想与方法，考查学生直观想象、逻辑推理、数学运算等核心素养以及分析问题、解决问题的能力[1].因此，2023年在注重备考策略、备考常规及转向的同时，备考实践中，要从这些方面去把握“题”的分类与导向作用，选出具有代表性的、方向性的试题深入分析解析几何的本质、基本思想与方法，切忌“题海战术”.

1素养立意下的备考分析

《普通高中数学课程标准（2017年版2020年修订）》明确给出了解析几何这一专题版块的内容要求，即能够根据不同的情境，建立平面直线和圆的方程，建立椭圆、双曲线、抛物线的标准方程，能够运用代数的方法研究上述曲线之间的基本关系，能够运用平面解析几何的思想解决一些简单的实际问题，从而可以从解析几何研究的两个问题——根据条件求曲线的方程、根据曲线方程研究性质来把握备考方向.

1.1总结归纳，把握备考方向

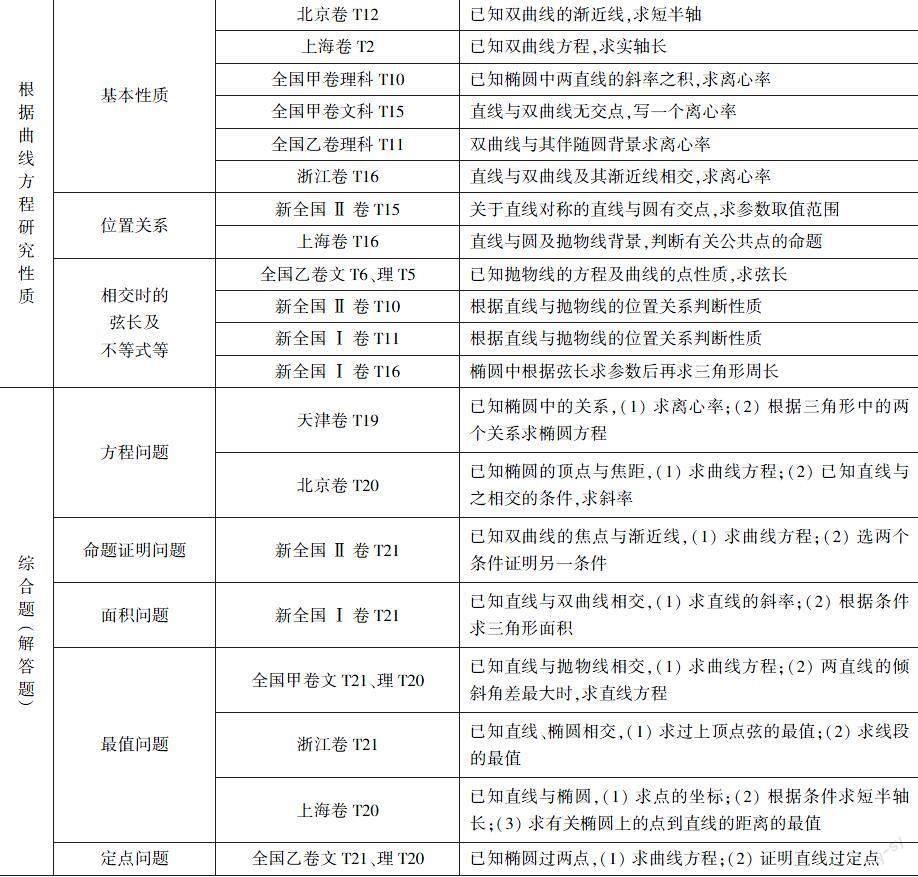
2022年高考数学对圆锥曲线与方程的考查，继续以圆锥曲线的定义、标准方程和几何性质为载体，以基本概念，通性、通法为考查重点，落实“基础性、创新性、综合性、应用性”的考查要求，实现了对学生必备知识、关键能力和学科素养的全面考查，对今后的课堂教学和复习备考都起到了积极的引导作用．为了方便把握备考复习方向，以下给出2022年各地高考试题中解析几何专题内容的考查分析统计表（表1）.

从以上统计的结果来看，每套真题卷几乎都能覆盖解析几何的所有知识点，其中基础题依然考查根据条件求曲线的方程，以及根据曲线方程研究基本性质；综合题还是聚焦几种常见题型，即求方程与性质命题的证明、与解三角形融合的面积问题、与函数思想融合的最值问题、有关定点定值的探究性问题等．

对近几年的高考命题特点以及备考策略，很多文献已有精心探讨（具体可参考文[1][2][3]）．针对2023届高三数学的解析几何专题的备考复习，除了夯实基础知识，掌握思想方法，积累基本经验外，相应专题复习时的重点、难点值得特别关注.

1.2类化解法，注重方法迁移

解析化是实现用代数方法解决几何问题的关键环节，考查学生的推理论证和运算求解能力．在具体的解析化过程中，解题要能够从数量与数量关系、图形与图形关系角度出发，挖掘数量与图形及其关系的内涵特征，将几何问题坐标化，并最终转化为代数式，通过代数推理与运算得到代数结论，解决几何问题．素养导向的高考试题不仅强调知识和智力，更强调知识的迁移和后天的习得.

例1（2022年浙江卷第21题）如图1，已知椭圆x212+y2=1．设A，B是椭圆上异于P（0，1）的两点，且点Q0，12在线段AB上，直线PA，PB分别交直线y=－12x+3于C，D两点．

（1）求点P到椭圆上点的距离的最大值；

（2）求|CD|的最小值．

评注此题第（1）问考查两点距离公式，第（2）问考查弦长公式，解题方法灵活，但两问落脚点都是最值问题，将函数思想与解析几何融合，突出了高考考查的综合性与创新性．以下通过设问方式、情境设置的变化，创设新的情境，变换设问角度和知识的组合方式，提升学生的科学探究能力和创新能力，发展学生的数学核心素养．

例2已知椭圆x212+y2=1．设A，B是椭圆上异于P（0，1）的两点，且点Q0，12在线段AB上，直線PA，PB分别交直线y=－12x+3于C，D两点．

（1）证明：kAP·kBP为定值；

（2）若直线BC过椭圆的下顶点H，求|CD|的值．

例3（长沙市2023届适应性考试第21题）设A，B是椭圆x22+y2=1上异于P（0，1）的两点，且直线AB经过坐标原点，直线PA，PB分别交直线y=－x+2于C，D两点．

（1）求证：直线PA，AB，PB的斜率成等差数列；

（2）求△PCD面积的最小值．

说明例2依然是例1中的椭圆方程，第（1）问是常规的定值问题，体现的是例1中性质的结论，简单考查了直线代入椭圆方程的一般计算步骤，同时也为第（2）问计算奠定基础，减少运算量．例3中改变了椭圆的方程与直线方程，命题立意与例1的探究结论保持一致．因此，本题很好的将最值问题迁移到了命题的证明，以及特殊情形时的几何量求值．

1.3强化运算，突破运算难点

在解析几何综合问题的解决过程中，直观想象和数学运算两大核心素养有着非常充分的体现．解析几何问题的解决一般是在几何分析的基础上通过运算达成的，而学生在运算方面的表现具有很大的差异．教师要把运算能力的培养贯穿于整个课堂教学，着重分析“如何想、怎样算”，让学生理解运算对象、掌握运算法则、探究运算思路、选择运算方法等，而不是把数学运算降格为数学计算，机械的套路化的解题训练．

例4（2022年新高考Ⅰ卷第11题）已知O为坐标原点，点A（1，1）在抛物线C：x2=2py（p>0）上，过点B（0，－1）的直线交C于P，Q两点，则（）.

A.C的准线为y=－1

B. 直线AB与C相切

C.|OP|·|OQ|>|OA|2

D. |BP|·|BQ|>|BA|2

评注本题强化对基础知识、基本技能和关键能力的考查．试题中的A选项实质考查抛物线的方程和准线，B选项判定直线AB为抛物线的切线方程，而C、D选项展示了直线与抛物线相交时的两个特殊性质．试题的四个选项涉及常规算法，如直线与曲线的位置关系，需要联立直线与曲线方程，利用韦达定理整体代换进行求解，所得表达式有时候可以很快求解，有时候就需要一些技巧，此时考生容易卡壳．

2知识点与试题类型预测

2.1选择题型（含多选）

试题1（本题考查直线平行的关系）已知直线l1：3x+（m+1）y－2=0与l2：mx+2y+2=0平行，则实数m的值是（）.

A．2B．-3

C．2或-3D．-2或-3.

试题2（本题考查直线与圆的位置关系）已知直线l：（x－1）cosθ+ysinθ=1，圆C：（x－1）2+y2=1，则直线与圆的位置关系为（）.

A．相交 B．相切 C．相离 D．不能确定

试题3（本题考查椭圆定义的应用）设F1，F2是椭圆C：x25+y2=1的两个焦点，O为坐标原点，点P在C上，且|OP|=2，则△PF1F2的面积为（）.

A．12B．1C．2D．3

试题4（本题考查抛物线定义的应用）设F为抛物线C：x2=2y的焦点，点A在C上，点B0，32，若AF=BF，则AB=（）.

A．1B．2C．32D．322

试题5（本题考查抛物线的焦点）设O为坐标原点，直线x=4与抛物线C：y2=2px（p>0）交于D，E两点，若∠DOE=60°，则C的焦点坐标为（）.

A．14，0B．13，0

C．12，0D．（2，0）

试题6（本题考查双曲线的基本性质与直接法求曲线方程）设F1，F2分别为双曲线x216－y2b2=1的左右焦点，已知双曲线的离心率为54，若点P满足kPF1·kPF2=－925，则点P的轨迹方程为（）.

A．x225+y216=1B．x225－y216=1

C．x225+y29=1D．x225－y29=1

试题7（本题考查椭圆的焦点三角形的性质）已知M（x0，y0）是椭圆C：x24+y2=1上的一点，F1，F2是C上的两个焦点，若MF1·MF2>0，则y0的取值范围是（）.

A．－22，22B．－33，33

C．－66，66D．－223，223

试题8（本题考查双曲线的离心率）已知F1，F2是双曲线C：x2a2－y2b2=1（a>0，b>0）的左、右焦点，A是C的左顶点，点P在过A且斜率为235的直线上，△PF1F2为等腰三角形，∠F1F2P=120°，则C的离心率为（）.

A．2B．3C．2D．3

试题9（本题考查双曲线的性质）设O为坐标原点，直线x=b与双曲线C：y2a2－x2b2=1（a>0，b>0）的两条渐近线分别交于D，E两点，若△ODE的面积为6，则C的焦距的最小值为（）.

A．2B．4C．43D．8

试题10（本题考查椭圆的离心率）设P是椭圆C：x2a2+y2=1（a>1）的上顶点，若存在以P为圆心的圆与椭圆C有四个公共点，则C的离心率的取值范围是（）.

A．0，22B．0，12

C．12，1D．22，1

试题11（长沙市2023届高三适应性考试第8题，本题考查圆与圆的位置关系）在平面直角坐标系xOy中，已知A（3，0），B（0，t）（t>0），若该平面中不存在点P，同时满足两个条件|PA|2+2|PO|2=12与|PO|=2|PB|，则t的取值范围是（）.

A．0，62－1B．62+1，+∞

C．62－1，62+1

D．0，62－1∪62+1，+∞

试题12（本题考查曲线方程的特征）已知方程x2cosα+y2=1，则（）.

A．当α=0°时，方程表示圆

B．当0°<α<90°时，方程表示焦点在y轴上的椭圆

C．当α=90°时，方程表示平行于y轴的两条直线

D．当90°<α≤180°时，方程表示焦点在y轴上的双曲线

试题13（本题考查双曲线的基本性质）已知M，N为双曲线4x2－y2+64=0的两个顶点，P是双曲线上的动点，则下列结论正确的是（）.

A. 渐近线方程为y=±12x

B. 离心率为52

C.直线PM与PN的斜率之积为14

D. 点P到两渐近线的距离之积为645

试题14（本题考查直线与椭圆方程的综合应用）已知点A为椭圆x24+y22=1的右顶点，O为坐标原点，过椭圆左焦点的动直线l与椭圆相交于P，Q两点，则（）.

A．|PQ|有最小值2

B．若OP⊥OQ，则直线l的斜率为2

C．直线AP与AQ的斜率之积为定值

D．△APQ的面积有最大值2+2

试题15（本题考查直线与抛物线相交时的性质探究）已知抛物线E：y2=2px经过点P（2，2），过点Q（0，1）的直线l与抛物线有两个不同的交点A，B，且直线PA交y轴于M，直线PB交y轴于N，设O为原点，QM=λQO，QN=μQO．以下结论正确的是（）.

A．抛物线E的方程为y2=4x

B．直线PQ与抛物线E相切

C．直线l的斜率范围为（－∞，0）∪0，12

D．1λ+1μ=2

2.2填空题型（含一题多空题）

试题1（本题考查抛物线和双曲线的定义）若抛物线y2=2px（p>0）的焦点是双曲线x23p－y2p=1的一个焦点，则p=．

试题2（本题考查双曲线的性质关系）已知双曲线C：x2a2－y2b2=1（a>0，b>0）的離心率为3，则C的渐近线为．

试题3（本题考查点到直线的距离公式）抛物线C：y2=2x上的点到直线y=x+3的距离的最小值为．

试题4（本题考查动直线与圆的位置关系）若直线l：x－my+m－1=0与圆C：（x－1）2+y2=4相交于A，B两点，则△ABC的面积的最大值为．

试题5（本题考查直线与圆相交时的性质）已知圆x2+y2=4上恰有四个点到直线y=x+b的距离都等于1，则实数b的取值范围是．

试题6（本题考查两圆的公切线方程）写出一条圆x2+y2=1与圆（x－4）2+y2=4均相切的直线方程．

试题7（本题考查圆的几何意义及基本不等式的应用）已知x，y∈（0，2），那么x2+y2+x2+（y－2）2+（x－2）2+y2+（x－2）2+（y－2）2的最小值为．

试题8（本题考查圆的方程）已知等腰三角形ABC的顶点A（2，0），底边一个端点B（1，3），C点的轨迹方程为．

试题9（本题考查直接法求点的轨迹方程）已知椭圆x225+y216=1与直线l：y=kx+m有唯一的公共点M，过点M且与l垂直的直线分别交x轴、y轴于A（x，0），B（0，y）两点．当点M运动时，点P（x，y）的轨迹方程为．

试题10（本题考查双曲线的离心率）双曲线C：x2a2－y2b2=1（a>0，b>0）的左顶点为A，点P，Q均在C上，且关于y轴对称．若直线AP，AQ的斜率之积为－14，则C的离心率为．

分析由kAP·kAQ=yA2－xA2+a2=－b2（a2－x12）a2－xA2+a2=－b2a2=－14，可求C的离心率e=52．

试题11（本题考查抛物线焦半径的长度关系）过抛物线y2=2px（p>0）焦点的直线AB交抛物线于A、B两点，若满足|AF|<|BF|，且|AF| 、|BF| 、|AB|成等差数列，则直线的斜率为．

分析由|AF|+|AB|=2|BF|，得|BF|=2|AF|，|AB|=2|AF|，结合抛物线的定义可得kAB=±22．试题12（本题考查直线与曲线的位置关系）已知椭圆Γ：x2m2+y23=1（m>0，m≠3）．过椭圆Γ上一点P作斜率为3的直线，与双曲线y25m2－x25=1有一个公共点，则m的取值范围为．

分析设直线y=3x+t，联立椭圆方程整理得（3m2+3）x2+23tm2x+（t2－3）m2=0，由Δ≥0，可得t2<3m2+3①；联立双曲线整理得（3－m2）x2+23tx+（t2－5m2）=0，由Δ=0，可得t2=5m2－15②．综合①②，解得m∈（3，3．

试题13（本题考查直线与双曲线相交时的定值问题）过双曲线x25－y24=1的右焦点F的直线与双曲线右支相交于A、B两点，线段AB的垂直平分线与x轴相交于点D，则|AB||DF|= ．

试题14（本题考查直线与直线，圆与圆的对称性）已知直线l：3x－4y+5=0，则与直线l关于x轴对称的直线的方程为；与圆x2+y2+4x－12y+39=0关于直线l对称的圆的方程．

图2试题15（本题考查几何法定义椭圆的方程）如图2是数学家Germinal Dandelin用来证明一个平面截圆锥得到的截口曲线是椭圆的模型．在圆锥内放两个大小不同的小球，使得它们分别与圆锥的侧面与截面都相切，设图中球O1，球O2的半径分别为4和2，球心距离|O1O2|=210，截面分别与球O1，球O2相切于点E，F，则截口椭圆的焦距为；椭圆的长轴为．

分析设O1O2与EF相交于点M，由Rt△O1EM∽Rt△O2FM，可得|MF|=23，|ME|=43，则2c=|EF|=2；设球O1，球O2与圆锥母线分别相切于点T，S，可求得2a=|TS|=6．

试题16（本题综合考查直线与圆的位置关系）已知圆M：（x－1）2+（y－1）2=4，直线l：2x+y+2=0，P为l上的动点，则|PM|的最小值为；过点P作圆l的两条切线，切点为A，B，当四边形MAPB的周长最小时，直线AB的方程为．

分析如图3，结合题意，当|PM|最小时，四边形MAPB的周长最小，且|PM|min=5，此时AB‖l．结合勾股定理，利用点到直线的距离公式可求得直线AB的方程．

试题17（本题考查抛物线的正交弦长关系）已知F为抛物线C：y2=2x的焦点，过F作两条互相垂直的直线l1，l2，直线l1与C交于A，B两点，直线l2与C交于D，E两点，①1AB+1DE=；②AB+DE的最小值为．

分析设直线l1方程为y=kx－12 ，联立方程利用韦达定理求得AB=2k2+2．同理，DE=2k2+2．从而1AB+1DE=12k2+2+12k2+2=12；AB+DE=2k2+2k2+4≥8，当且仅当k=±1时等号成立，即AB+DE的最小值为8．

2.3解答题型

试题1（本题考查了定义法求曲线的轨迹方程，以及直线与曲线的位置关系等）已知圆C1：（x+5）2+y2=25和圆C2：（x－5）2+y2=1，动圆C同时与这两个圆相外切．

（1）求动圆圆心C的轨迹Γ；

（2）过点B（1，0）的两条直线l1，l2，其中l1与Γ相切于点A，l2与Γ相交于的P，Q两点．求证：|BP|·|BQ|>|BA|2．

试题2（本题以抛物线为背景，考查对定点定值问题的处理求法）已知O为坐标原点，过点P（1，0）的直线l与抛物线E：y2=6x相交于A，B两点．

（1）判断直线OA与直线OB的斜率之积是否为定值；

（2）若点Q（2，0），连接AQ并延长交E于点C，连接BQ并延长交E于点D，求证：直线CD过定点，并求出定点坐标．

试题3（长沙市2023年适应性考试第21题，本题以椭圆为背景，考查相关性质的证明以及最值问题的求解）设A，B是椭圆x22+y2=1上异于P（0，1）的兩点，且直线AB经过坐标原点，直线PA，PB分别交直线y=－x+2于C，D两点．

（1）求证：直线PA，AB，PB的斜率成等差数列；

（2）求△PCD面积的最小值．

试题4（本题以双曲线为背景的结构不良形式呈现，考查相关性质的推理论证）已知双曲线C：x2a2－y2b2=1（a>0，b>0）的实轴长为2，且焦点到渐近线的距离为3．

（1）求双曲线C的方程；

（2）若直线l与双曲线左右两支分别交于M，N两点，给出下列三个论断：

①直线l过双曲线C的焦点； ②直线l与圆O：x2+y2=a2相切； ③|MN|=3．

以其中的一个论断作为条件，证明余下的两个论断互为充要条件．

3结语

素养立意的高考命题重视学科观念、规律的考查，考查学生扎实的学科基础，引导他们去形成思维中的惯性观念，并且能够合理的进行转化，将这些学科知识作为素养养成和发展的基础和先决的条件[4].由于不同的教学经验、不同的学生都会产生不同的解题教学过程，再加之从能力立意到素养立意的转变体现了“从关注知识”到“关注人”的转变，因此，备考实践中，一定要根据不同学校、不同层次学生的基础实践，聚焦“最近发展区”，才能起到“事半功倍”的效果.

參考答案

一、选择题

1.A；2.B;3.B;4.B；5.B；6.C;7.B;8.C;9.C;10.D;11.D;12.ACD；13.BD;14.ACD;15.BD.

二、填空题

1.16;2.y=±2x；3.524；4.2；5.（－2，2）；

6.y=1515x+41515，y=－1515x－41515，y=377x－477，y=－377x+477，写其中一条即可.

7.42；8.x2+y2－4x－6=0（x≠1）；9.25x281+16y281=1（y≠0）；10.52;11.±22；12.（3，3］；13.253；

14.3x+4y+5=0；（x－4）2+（y+2）2=1（或x2+y2－8x+4y+19=0）；15.2，6；16.5；2x+y+1=0；17.12；8.

三、解答题

略.

参考文献

［1］周威.素养立意下解析几何专题复习常规与转向[J].中学数学杂志，2022（03）：62-65.