二次函数中三角形面积最值问题的解题策略

张晓

【摘要】初中数学教育在素质化进程中不断改革，教学过程中素质教育的理念渗透越来越强.既往开展的初中数学教学，以二次函数问题为例，传统教学方式的不足越来越显著，并没有从数学核心素养的角度切实提升学生的学习能力.本文针对初中数学函数教学中存在的不足进行分析，从二次函数中三角形面积最值的问题入手，从多元化解题思路的角度为优化数学函数解题教学提出建议.

【关键词】二次函数；数形结合；解题

随着初中阶段新课程改革进程持续推进，数学课改中将对学生的素质教育作为重点发展方向.但目前初中阶段的二次函数教学仍以常规的教学方式为主导，学生在面对二次函数问题时思路不够灵活，方法不够多样.长此以往，学生可能逐渐失去对数学学科的学习兴趣，学习态度不够积极，成绩下降[1].教师及时发现该问题并积极讨论研究，在函数教学实践中优化教学模式，提升学生解题能力成为一项热点课题.

素质教育下，数学学科的教学工作应将重点放在培养学生多元化解题能力、提升学生数学学习积极性、满足学生全方面发展的需求上.以二次函数中三角形面积的最值问题为例，教学过程中教师可以通过改良教学方法，引入新的教学模式，给数学教学注入新的活力.这样有助于引导学生逐渐形成多元化的逻辑思维能力，解题思路更灵活多样，对数学产生更浓厚的学习兴趣，提升学生学科成绩及综合素养.

1 初中数学二次函数解题思路与多元化解题

初中阶段，学生不同程度地了解了函数相关知识内容.年级升高后，函数内容也将迎来更高的难度.学生理解抽象特征更显著的内容，解答函数问题需要的理解力、学科素养都高出一个等级.部分学生在二次函数相关问题的学习中成绩不佳，可能是因为自身理解能力不足、学习方式不正确，也可能是因为教师采用的教学方式陈旧、死板.这些问题普遍存在于各级初中学校的二次函数教学实践中.学生在遇到解题方式自由度较高的问题时，会出现很大的困扰，解题时容易被固定思维所限制，不能运用数学思想观念看待和解答问题，最终的结果就是解题效率和正确率不高[2-3].

多元化的解题方法，重视的是解题方式的创新与探索，要求学生遇到不同的题目时能灵活地变换解题方式，临危不惧.以二次函数中的三角形面积最值问题为例，教学中引入多元化的教学方式，以多元化的涵义为出发点，引导学生从简单角度理解问题，用数学思想看待问题，在方法中融入课本基础知识，切实发挥多元化教学模式效果，提升教学成效.

2 二次函数中三角形面积最值函数内容的难点

初中学生在函数内容学习中，求函数解析式的难度较高.这是因为部分学生解题思路单一、固定，面对求解函数问题时的首选方式就是通过一般表达式解析，而对函数交点式和顶点式的解析式不够熟悉，运用不熟练[5].一旦题目中限制了函数解析式的使用类型，这部分学生可能会手足无措，解决与数形结合相关的问题难度大，正确率低.初中阶段函數的学习内容中，除了要求学生掌握函数基础概念与公式，还涉及数与形的结合等内容.但部分学生对二次函数知识尚未建立起完整的知识体系，突然面对综合性题目，很难在短时间内理解和解答问题[6-7].

分析近年来各大知名初中学校校内的二次函数试题以及省中考试题，发现二次函数相关的应用题考查分数占比较高，题目对学生的理解和数形结合能力有较高的要求，解题方法往往不固定.分析学生对这类问题的解答，发现第一小问概念性较强，学生如果熟悉函数基础概念与公式，就能快速、准确答题.而第二小问中的难度较高，是因为题目的综合性较强，学生难以把握题目中的关键信息，难以找到最简便的解题方法，可能在这一题上耗费较长的时间，可能回答错误.

3 初中数学二次函数中三角形面积最值问题的教学策略

3.1 强化对学生转化思维的培养

为了让学生能高效率、高质量地完成函数部分的学习，学习效果果稳健提升，教师应重点关注学生对数学的兴趣，并通过引入多种教学方法，帮助学生在面对不同类型的问题时，能灵活应用不同方法，既快速又准确地解答各类函数问题.学生在数学学习热情的影响下，遇到难题时才不会产生挫败感和厌烦的心理，而是会坚持主动寻求问题的最佳解题方式.

初中二次函数教学中，常用的教学方式有联系日常生活、转化思维能力等.联系日常生活可以将课本上的函数问题具象化，让学生的视野不必再拘泥于教材中的内容，让学生脱离函数中的抽象性，这样有助于培养学生的逻辑思维能力.转化思想实质上是一种面对不同类型的问题时，能够采取某一种转化的方法.转化的历程，能让学生在面对难度高、陌生的问题时，联系自己熟悉的问题或是有简便解题方法的问题.这样的思想方法在学习过程中的实际运用，将大大提升学生学习效率和效果[8]

下面以一道二次函数中三角形面积最值的问题为例，分析教学中转化思维的解题方式.

例 如图1所示，在平面直角坐标系中，抛物线y=ax2+bx+2（a≠0）与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，抛物线经过点D（-3，-2）和点E（3，2），点P为第一象限抛物线上的动点.

（1）求图中抛物线的表达式；

（2）当△BPC的面积取最大值时，求△BPC面积及点P的坐标.

将点D、点E左边代入函数表达式，解得函数表达式为：y=-29x2+23x2+2.

（1）补形法：用补形方法把不规则图形转化成规则图形，如图2，将斜三角形面积转化成矩形面积减去三角形的面积.过点P作PM⊥y轴，垂足为M.过点B作BN⊥PM，垂足为N，四边形OBNM为矩形，则利用定点的横纵坐标，求得三角形面积.

（2）分割法：以转化的思想将斜三角形分割成底与高分别与坐标轴平行的三角形，充分利用定点的横纵坐标来求三角形面积.过点P作PE⊥x轴于点F，△BPC就分割成△HPC和△HBP.过点C作CD⊥PF于点D，过点B作BE⊥PF，如图3所示.

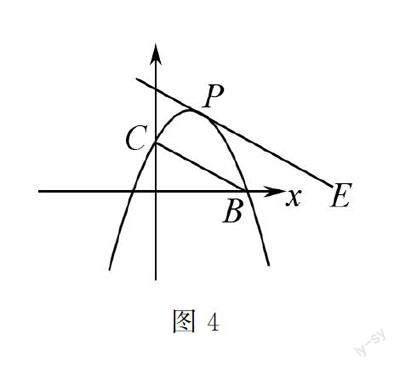
（3）平行线法与切线法：以补形和分割方法为基础，可以延伸、转化出平行线法与切线法.以切线法为例，如图4，若P点在抛物线上使△BPC的面积达到最大值，须使PE∥BC且与抛物线有且只有一个交点.P点在抛物线上，PE与抛物线有且只有一个交点时，BC边上的高才最大.

从以上用转化思维解决二次函数中三角形面积最值的问题中，可以发现转化思想方法广泛地蕴含于数学内容之中.为了便于学生发现和理解，教师在教学这部分内容时需要切实从教材的知识出发，指导学生如何运用转化思想在教材上的众多知识内容之间建立关联.这样学生就可以对教材内容建立明确、具体化的知识架构，提升学生对数学知识的记忆与理解能力，在遇到各类问题时能快速、灵活调用学到的知识，在原有的学习内容的基础上对转化思想、数形结合思想有更深刻的认识，有更灵活的运用能力[9].

初中阶段为学生安排的教学活动，往往具有一定的规律，那就是先一般后特殊、先简单后复杂、先直观后抽象.如果能将转化思维的教学同教学活动的开展规律协调一致，形成思想方法与具体教学内容的有机融合，将有效增进学生对抽象化的数学问题的理解，从而提升学生对实际问题的掌握和解决能力.

3.2 信息技术呈现，数形结合过程具象化

二次函数中的三角形面积最值问题，属于函数与图形有关的问题，常规的教学方法下很大一部分学生很难直接在脑海中构建出图形结构.课堂教学过程中，如果教师能将教具、新媒体技术引入课堂环境中，以更加直观的方式将教学内容呈现在黑板或多媒体上，能让学生在初步接触这类知识时省去自主想象图形结构的过程，直接观察后接受新的数学知识，更便于起步阶段的学习理解.久而久之，学生就能习惯根据题目直接构思图形结构，逐渐形成函数知识的形象化思维能力.

在函数等内容的课堂教学中引入多媒體技术，还有一点优势就是有助于形成良好的课堂氛围[10].师生、生生间的互动过程，需要借助课堂智慧互动与信息设备间的多元互动，避免较为枯燥的学习内容招致学生的抵触、反感，让学生以兴趣为导向逐步融入数形结合思想氛围中，感受数形结合思想在二次函数三角形面积最值问题中的应用优势.让学生在交流与互动中找到以往二次函数方面学习的不足，带着思考调整学习方法，发展转化的学习思想.

4 结语

结合以上的分析内容，可知在学习函数相关内容时，学生学习起来难度较高是很正常的现象.这是因为二次函数这部分内容具有显著的抽象性特征，但学生面对的题目又常常是联系实际应用的类型，增大了理解与解题难度.目前初中数学二次函数的教学方法，存在可改进之处.例如在二次函数中三角形面积最值问题的教学中，就可以引入数形结合的教学方式，引导学生以转化、分割等思维灵活解题，学会多种解题思路.这样在实际应用中就可以根据题型和题目与实际相结合的特点，选取更加适宜的方式解决问题.这样解题思路清晰，得到的答案既准确又高效.

教师应围绕二次函数内容积极探索前沿教学方法，在教学过程中注重培养学生的数形结合思维，让学生从二次函数中三角形面积的最值问题开始，将学习方法沿用到其他的数学内容学习中，逐渐能自主进行多角度、多方法解题，提升数学学习效果和学科综合素养.

参考文献：

[1]丁力.初中数学几何最值问题探究——以“将军饮马”问题模型的解题策略为例[J].数学教学通讯，2020（14）：79-80.

[2]吴建惠，周敏刚，李硕.始于“活动”，成于“转化”，促深度学习——以“最短路径问题”的教学为例[J].数学教学通讯，2022（14）：9-11.

[3]曾慧.“双减”政策下信息技术与初中数学教学融合应用——以数学活动“两个特殊两位数相乘的积的规律”为例[J].广东教育（综合版），2022（7）：48-49.

[4]裴娥.基于数学学科核心素养的初中数学解题教学研究——以2020年浙江省金华市中考数学第24题为例[J].理科考试研究（初中版），2021，28（1）：2-4.