不同重建深度的微图像阵列生成

杨翠妮，李姣姣，郭兆达，邓 欢

（四川大学 电子信息学院，四川 成都 610065）

1 引 言

集成成像技术是目前最热门的裸眼真三维显示技术之一，它避免了立体视疲劳问题，可以实现全视差、连续视点的真三维立体成像且无需佩戴眼镜等辅助设备［1-6］。集成成像可以分为记录和再现两个过程。在记录过程中，3D 信息被透镜阵列采集，并被编码为微图像阵列；在再现过程中，3D 信息从微图像阵列解码，并重建3D图像。微图像阵列包含3D 图像的位置和角度信息，以产生正确的深度线索，缓解辐辏调节冲突。

自1908 年首次提出集成成像技术以来［7］，已经出现了多种生成微图像阵列的方法，计算机生成集成成像技术引起了人们的关注［8-10］。Halle 提出了一种多视图渲染算法，该算法从多个角度渲染静态场景，并且来自同一视点的每组光线都使用透视投影模型进行渲染［11-12］。Jung 和Koch 提出了一种基于图像渲染和深度补偿插值的光场图像高效渲染方法［13］。Deng 等人介绍了一种稀疏相机阵列生成微图像阵列的方法，可以将其视为两步微图像阵列生成［14-15］。Ji 等人专注于倾斜的微图像阵列生成方法，以减少摩尔纹的影响［16］。Li 等人引入一种多正字视锥体组合的实时计算机生成集成成像方法，充分利用了图形处理单元的可编程性来提高计算效率［17］。Sang 等人提出了一种基于逆向光线追踪的高效计算机生成方法，可以认为这是实时和交互式计算机生成集成成像的一种有效途径［18］。为了在交互基础上生成高质量的3D 图像，Sang 等人还提出了一种基于路径追踪蒙特卡罗方法和递归卷积神经网络的微图像阵列生成方法［19］。在计算机集成成像微图像阵列生成过程中，设置的相机阵列参数需与3D 物体尺寸以及系统景深相匹配，因此针对于不同的3D 显示系统参数，需要重新生成对应的微图像阵列，势必会增加图像生成的复杂度。

本文分析了集成成像技术中3D 像点重建深度与同名点视差的内在联系，结合图像元节距与同名点视差以及3D 深度的关联关系，提出了一种基于图像元缩放变换的不同重建深度微图像阵列生成方法。对于不同的显示系统，无需对目标三维场景进行重新采集，通过简单的图像元节距调整，等效改变同名点像素的视差值，从而改变了光场的采样间隔，使得新节距下的微图像阵列可适配不同景深的集成成像显示系统，提升了微图像阵列的实用性。

2 集成成像立体深度与同名点关系

在集成成像记录过程中，3D 场景中某一物点被多个透镜元记录在其覆盖的图像元中形成同名点，所有透镜元记录的图像组成了微图像阵列。在集成成像再现时，同名点间的视差值反应了3D 物点的深度信息，如图1 所示，3D 像点的重建深度l与微图像阵列中同名点视差T、显示面板到透镜阵列的距离g及透镜阵列中透镜元节距plens有关。它们之间满足：

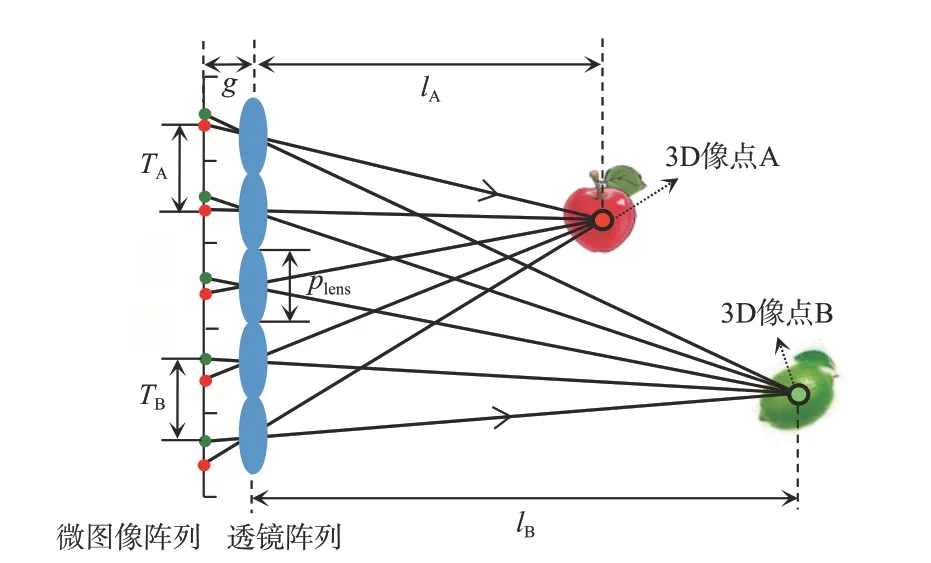
图1 集成成像显示过程中3D 像点与同名点视差的关系Fig.1 Relationship between 3D image point and parallax of homonymous points in integral imaging display

当系统参数一定时（以g=13.2 mm、plens=14.7 mm 为例），3D 像点的重建深度随同名点视差的变化曲线如图2 所示。

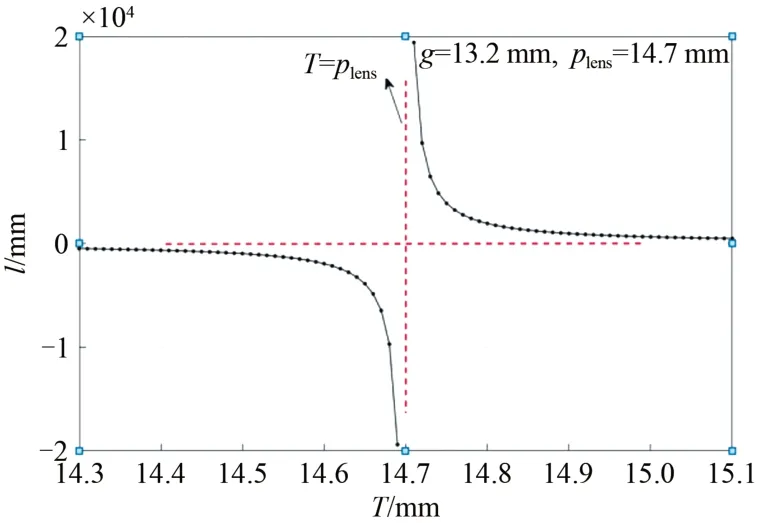
图2 3D 像点的重建深度随同名点视差的变化曲线图Fig.2 Variation curve of reconstruction depth of 3D image point with parallax of homonymous points

由图2 和公式（1）可知：以显示方向为正方向，当T＞plens时，l＞0，即重建的3D 图像具有正的深度值，浮出屏幕。如图3（a）所示，“苹果”和“青柠”上的两个像点所对应的同名点视差均大于透镜元节距，因此两者均凸出屏幕显示。当T=plens时，l趋向于无穷，通常不会出现此类3D 图像。当T ＜plens时，l＜0，即重建的3D 图像具有负的深度值，凹进屏幕里面，如图3（b）所示，“苹果”和“青柠”上的两个像点所对应的同名点视差均小于透镜元节距，因此两者均凹进屏幕显示。

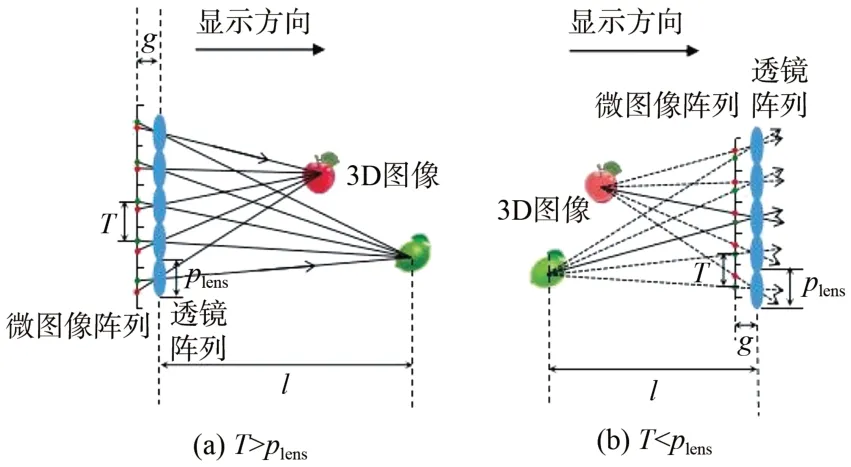
图3 3D 像点重建深度与同名点视差的关系Fig.3 Relationship between reconstruction depth of image point and parallax of homonymous points

3 不同深度的微图像阵列生成

根据以上分析容易发现，在系统参数（plens，g）一定时，3D 像点的重建深度与同名点视差具有非线性的负相关关系，可以通过改变同名点视差值反过来改变3D 像点的重建深度。然而集成成像显示系统具有有限的景深，当超出系统可以承载的景深范围时，重构的3D 像点会弥散得模糊不清。因此在视差调节时，还需要考虑到3D像点重建深度范围。如图4 所示，根据集成成像显示系统3D 景深范围的限定，确定可接受的最大及最小的3D 像点重建深度分别为：

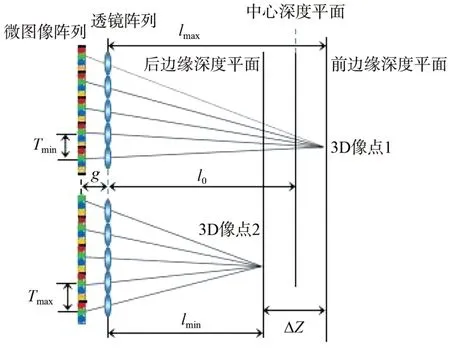
图4 同名点视差的变化范围Fig.4 Variation range of parallax of homonymous points

式中，l0为透镜阵列到中心深度平面的距离，可由高斯成像公式推导，具体为l0=ΔZ为显示系统的景深。结合公式（1），推导出可清晰显示3D 图像的同名点视差的最小及最大值分别为：

基于上述分析，本文提出了一种基于图像元缩放变换的不同重建深度微图像阵列生成方法以适配不同景深范围的集成成像显示系统。由于同名点视差与图像元节距具有正相关关系，可以对图像元进行缩放变换得到新的同名点视差T'：

其中，η为图像元缩放比例并由公式（1）得出新的重建深度l'：

考虑实际透镜和像素配置时深度为离散值，在对图像元进行缩放变换时，ηT需对应像素尺寸的整数倍，因此公式（5）的离散表达式为：

其中：［*］表示四舍五入取整，px表示显示面板像素尺寸的大小。

根据公式（1）和（5），我们得出原有深度l和新的深度l'的函数关系：

3D 像点重建深度随图像元缩放比例的增大而减小，如图5 所示。以g=13.2 mm、plens=14.7 mm为例，在图5（a）中，图像元缩放比例η=1，红色的同名点发出的光线经透镜阵列调制后，在空间中会聚形成3D 像点，重建深度为l。在图5（b）中，图像元缩放比例η=1.12，3D 像点的重建深度l'减小为0.4l。在图5（c）中，图像元缩放比例η=0.95，3D 像点的重建深度l'增大为2.5l。

图5 不同图像元缩放比例的3D 像点重建深度Fig.5 3D image reconstruction by elemental image array with different scalings

虽然图像元缩放比例η的变化值很小，但重建深度的变化却很大，如图5 所示，其沿透镜光轴方向的轴向放大率α为：

轴向放大率α与原有图像深度l、g及图像元缩放比例η有关，而原有图像深度l限制在系统景深范围之内，（η-1）l的变化值较小，可以用中心深度平面处的轴向放大率近似为整个3D 图像的轴向放大率，因此轴向放大率α可近似为：

3D 图像垂直于透镜光轴方向的垂轴放大率为β：

由公式（10）可知，当η≠1 时，3D 图像的轴向放大率和垂轴放大率不同，存在一定程度的压缩或拉伸。然而，在对3D 图像进行深度变换时，η的值接近1，变化范围在5%左右，其轴向放大率α与垂轴放大率β近似相等，可看作是角大小不变的深度变换，不会产生明显的3D 图像畸变。

在如图6 所示的集成成像显示系统中，将微图像阵列A 通过图像元缩放变换获取两张新的微图像阵列，分别为微图像阵列B 和C，当微图像阵列A、B、C 分别在显示面板上显示时，无需进行系统器件参数的调节，便可以显示出不同重建深度的3D 图像。

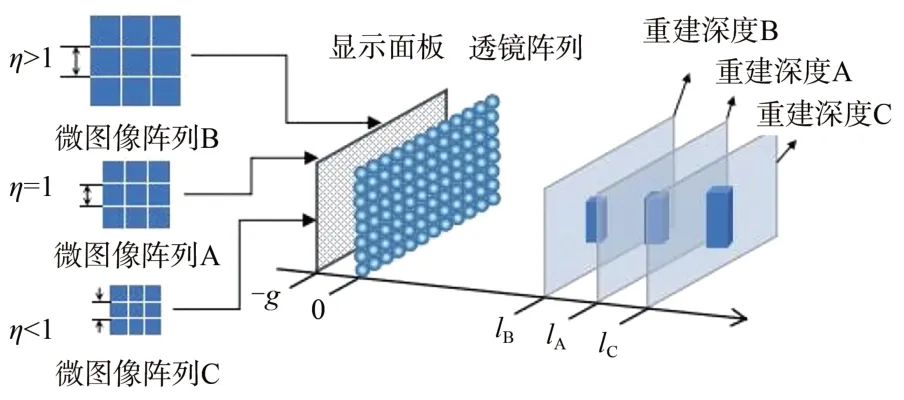
图6 显示系统的结构及原理示意图Fig.6 Structure and principle diagram of the display system

4 实验验证

我们利用3Ds Max 软件搭建了3D 场景及拍摄相机阵列，如图7 所示。所拍摄的3D 场景由字符“3”和字符“D”组成。搭建了虚拟相机阵列进行光场信息的获取，将中心深度平面设置在距离拍摄相机阵列145 mm 的深度位置。字符“3”和字符“D”分别在中心深度平面前、后2 mm 处。

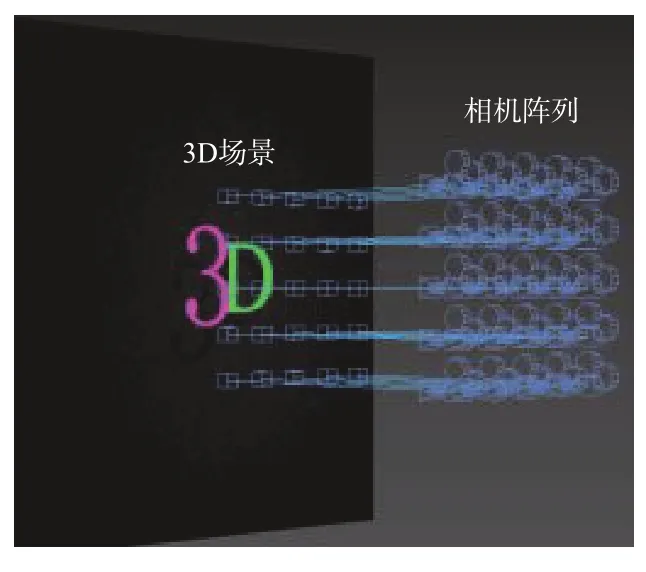
图7 3D 拍摄示意图Fig.7 3D shooting diagram

获取的微图像阵列A 如图8（a）所示，图像元缩放比例η=1。利用本文所提出的方法，得到缩放比例η=1.01 的微图像阵列B 和η=0.99 的微图像阵列C，分别如图8（b）和图8（c）所示。

图8 微图像阵列Fig.8 Generated elemental image arrays

为了验证本文所提方法的正确性，选择基于深度的计算机再现方式进行3D 再现，实验参数如表1 所示。利用获取的3 张微图像阵列分别进行了基于深度的计算机集成成像再现实验，重建的3D 图像如图9所示。图9（a）所示为η=1的微图像阵列A 重建的3D 图像，在143～147 mm 深度范围内，如图中红色方框所示，字符“3”在147 mm的深度上清晰再现，字符“D”则在143 mm 的深度上清晰再现。图9（b）所示为η=1.01 的微图像阵列B 重建的3D 图像，字符“3”与字符“D”分别在深度130 mm 和127 mm 处清晰再现，说明通过图像元节距的增大可以实现3D 图像深度的缩小，且具体深度值的变化符合理论公式（5）的推导。图9（c）所示为η=0.99的微图像阵列C重建的3D 图像，字符“3”与字符“D”分别在深度167 mm 和162 mm 处清晰再现，说明通过图像元节距的缩小可以实现3D 图像深度的增大，且具体深度值的变化符合理论公式（5）的推导。根据实验结果分析可得：当图像元做放大变换后，3D 图像的重建深度减小；当图像元做缩小变换后，3D 图像的重建深度增大。该实验结果验证了本文所提出方法的正确性及可行性，即通过图像元缩放变换可以实现不同重建深度的3D 图像重建。

表1 基于深度的计算机集成成像再现实验的参数列表Tab.1 Parameter list of the depth-based computer integral imaging reconstruction

图9 重建的3D 图像Fig.9 Reconstructed 3D image

5 结 论

本文分析了集成成像技术中3D 像点重建深度与同名点视差的内在联系，提出一种基于图像元缩放变换的不同重建深度微图像阵列生成方法。该方法针对不同景深范围的集成成像显示系统，无需重新进行集成成像拍摄，仅通过对微图像阵列进行简单的节距变换处理就可以改变重建3D 图像的深度，使微图像阵列可以与不同景深的显示系统相适配，增加了微图像阵列的实用性。通过基于深度的计算机再现实验证实了3 个不同重建深度范围的3D 图像重建，验证了所提方法和理论推导的正确性。本方法可以在一次集成成像拍摄的情况下，实现不同深度的3D 图像再现以适配显示系统的3D 景深，最大化发挥系统景深性能。