局部系数增强判别协同表示分类法

简彩仁,夏靖波

(厦门大学嘉庚学院,福建 漳州 363105)

模式分类是机器学习的重要研究方向,许多分类方法,比如支持向量机、随机森林等需要训练分类器,在追求准确率的同时容易产生过拟合问题[1].基于表示理论的分类方法利用表示系数和最小误差准则[2]对测试样本进行分类,而不需要训练分类器,可以避免过拟合等问题,因此基于表示理论的分类方法得到了研究学者的青睐.基于表示理论的分类方法的关键在于求解表示系数.它的典型代表是Wright等[2]提出的稀疏表示分类法(SRC)和Zhang等[3]提出的协同表示分类法(CRC).SRC利用稀疏表示重构测试样本得到表示系数,而CRC利用岭回归模型求解表示系数,因此,CRC也称为最小二乘回归分类法(LSRC)[4].Xu等[5]利用人脸的轴对称性质对人脸图像进行修正,提高了SRC的人脸识别准确率.Xu等[6]提出两阶段人脸图像分类方法,利用选取近邻样本达到稀疏的目的,再利用CRC实现人脸图像分类.文献[3,7]对比了SRC和CRC两种方法构造的正则项对分类的影响.因为CRC可以得到解析解,计算简单并且可以得到理想的分类准确率,因此不同的学者提出了许多基于CRC的扩展模型[8-12].鉴于CRC求解表示系数的时候并没有考虑类别信息,而类别信息对于提高分类准确率具有重要意义,因此利用类别信息求解表示系数是对CRC的一种改进.概率协同表示分类法(ProCRC)[10]利用协同子空间的概率改进CRC,充分利用类别信息提高分类准确率.判别稀疏表示分类法(DSRC)[11]引入判别信息项进行改进,求解具有降低类间相关性、增强类内相关性的表示系数.判别协同表示分类法(DCRC)[12]整合ProCRC和DSRC的判别信息项,对CRC进行改进.

ProCRC、DSRC和DCRC从不同的角度引入类别信息改进CRC,因此,考虑类别信息求解表示系数可以在一定程度上提高分类准确率.借鉴ProCRC、DSRC和DCRC的思想,本文通过定义判别信息惩罚项以增强表示系数的判别能力,并基于近邻系数相似性定义局部系数强化项以增强近邻样本的协同表示能力,求解更加鲁棒的表示系数,提出局部系数增强判别协同表示分类法(LDCRC).

1 CRC及其改进模型

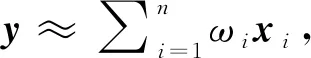
CRC利用岭回归模型[13]求解表示系数,其数学模型如下

(1)

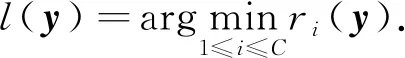
(2)

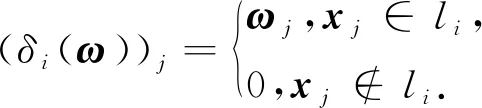
ProCRC[10]通过定义测试样本属于协同子空间的概率改进CRC,所有训练样本的C类标签集是l(X)={1,2,…,C},每一个训练样本x∈X和测试样本y的类别分别为l(x)和l(y),测试样本y属于类别c的概率定义为

P{l(y)=c}=P{l(y)∈l(X)}·P{l(y)=

(3)

其中:λ,γ>0是正则参数.如果y真的来自c类,公式(3)中概率P{l(y)=c}的最大化导致c类样本对y的表示和对y的分类有显著贡献.对公式(3)取对数,ω可以等价的用

(4)

DSRC[11]通过引入判别信息项改进CRC,如下:

(5)

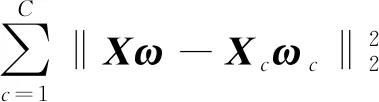
(6)

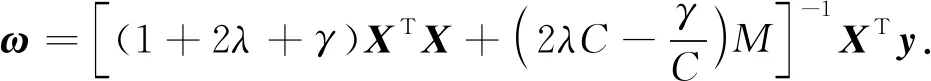
ProCRC、DSRC和DCRC都利用了类别信息改进CRC.基于类别信息,它们定义了不同的正则惩罚项,使求解的表示系数具有更强的判别能力.

2 LDCRC

针对CRC缺少类别信息的不足,借鉴DSRC和DCRC,定义判别信息惩罚项以增强表示系数的判别能力.同一空间下,两个相似样本的距离很接近,导致它们的表示系数有高度的相似性,基于这一发现,定义局部系数强化项以增强近邻样本的协同表示能力.基于判别信息惩罚项和局部系数强化项,提出LDCRC.

2.1 目标函数

受文献[10-11]的启发,为增强表示系数的判别能力,并考虑到DSRC和DCRC的解析解中含有类别数C,因此用C增强判别信息,定义判别信息惩罚项为

CTr(ωTMω),

(7)

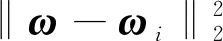
(8)

其中,K表示近邻样本数.

(9)

其中λ,γ>0是正则参数.公式(9)的第2项包含判别信息以增强表示系数的判别能力,第3项包含局部信息以增强近邻样本的协同表示能力,因此公式(9)既可以强化局部信息提高近邻样本的协同表示能力,又可以利用类别信息,提高判别能力.

2.2 模型求解

利用矩阵的迹Tr,将公式(9)写为

L(ω)=Tr[(y-Xω)T(y-Xω)]+

展开得

L(ω)=Tr(yTy)-2Tr(ωTXTy)+Tr(ωTXTXω)+

λCTr(ωTMω)+γKTr(ωTω)-

关于向量ω求导得

令其为0,得

(10)

因此,公式(10)为目标函数的解析解.

2.3 LDCRC算法

由于现实中的数据集往往是非线性的,因此基于欧式距离的相似度度量不够准确.基于CRC的表示系数,定义一种新的相似度.由公式(1)的解析解得到表示系数ω=(XTX+λI)-1XTy,定义相似度为

d=|ω|,

(11)

其中,|ω|为表示系数ω的绝对值,di=|ωi|=sim(xi,y)表示样本xi与测试样本y的相似度,越大的di=|ωi|说明xi在重构y时的作用越大,也意味着xi与y的相似度越高.

基于以上的讨论,将LDCRC归纳如下.

算法:LDCRC

输入：训练集X,类别数量C,待分类样本y,近邻样本数量K,正则参数λ,γ;

输入：y所属类别l;

Step1:由公式(11)得到相似度度量,并降序排列选择前K个样本为近邻样本;

Step2:由公式(10)得到表示系数ω;

Step3:利用最小重构误差准则,得到y的所属类别l.

2.4 模型比较

ProCRC、DSRC、DCRC和LDCRC都利用了类别信息定义了不同的判别惩罚项.

利用判别信息矩阵M,ProCRC的解析解可以写为ω=[(1+γ(C-2))XTX+λI+γM]-1XTy.

DSRC的解析解为ω=[(1+2λ)XTX+2λCM]-1XTy.

对比以上公式,不难发现4种方法都含有XTX和M,系数的大小反映了重构误差项和判别信息项在求解表示系数的影响程度.LDCRC考虑了近邻样本对求解表示系数的影响,以增强近邻样本的协同表示能力.因此,LDCRC保留了ProCRC、DSRC和DCRC的判别能力,又增强了近邻样本的协同表示能力.

3 实验分析

为验证LDCRC的分类性能,采用对比实验验证LDCRC的有效性.选用CRC、ProCRC、DSRC和DCRC作为对比方法.由于所有的方法都具有解析解,从运行效率上分析,各种方法的差别不大,故在实验中不比较各种方法的运行效率.

3.1 实验参数设置和实验数据

CRC、ProCRC、DSRC、DCRC和LDCRC都有正则参数,类似于文献[10],将正则参数λ和γ都设为0.001.当γ=0时,DCRC退化为DSRC,根据文献[11],本文将DCRC中的γ设为1.采用交叉验证方法对比不同折数下的分类准确率,交叉验证折数设为{2,4,6,8,10}.LDCRC的近邻样本数K设为5.

实验选用6个常用的标准图像数据集:AR_32x32(AR)、IMM_32x32(IMM)、LFW_32x32(LFW)、ORL_32x32(ORL)、PIE29_32x32(PIE29)、PolyU_Palmprint2_32x32(PolyU),其基本信息如表1所示.

表1 数据信息

3.2 结果分析

图1给出了不同交叉验证折数下各种方法的分类准确率.表2给出了各种方法在不同交叉验证折数下的分类准确率的平均值.

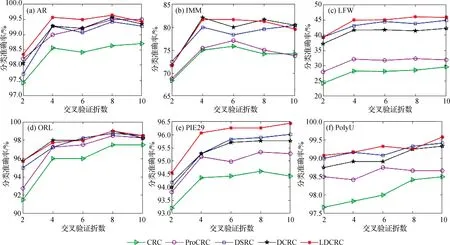
图1 不同交叉验证折数下的分类准确率Fig.1 Classification accuracies under different cross-validation folds

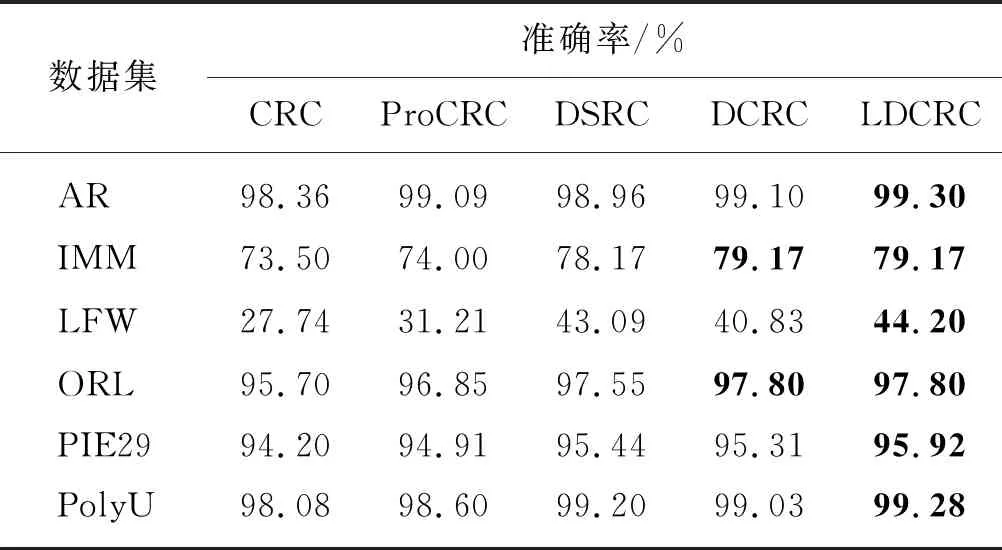
表2 平均分类准确率

从图1和表2的实验结果不难发现,CRC的分类准确率是最低的,而ProCRC的分类准确率优于CRC,这一实验结果表明考虑类别信息可以提高CRC的分类准确率.DSRC和DCRC的分类准确率优于ProCRC,这表明DSRC和DCRC的判别信息惩罚项可以降低类间相关性、增强类内相关性,从而提高分类准确率.LDCRC的分类准确率是最优的,这一结果说明,判别信息惩罚项可以保持DSRC和DCRC的优点,而局部系数强化项可以加强近邻样本的协同表示作用,更好地增强近邻样本对测试样本的影响,使求解的表示系数有较好的表示能力,从而提高分类准确率.DCRC在IMM和ORL两个数据集的分类准确率与LDCRC的相当,但是在别的数据集上,DCRC分类准确率低于LDCRC.一种可能原因是,IMM和ORL的样本数量较少,LDCRC选取的近邻样本产生的协同表示能力不足.因此本文提出的LDCRC对提高CRC、ProCRC、DSRC和DCRC的分类准确率是有效的.

3.3 参数讨论

本节讨论正则参数λ和γ对LDCRC的影响.图2给出了在交叉验证折数为6,不同的参数λ和γ下,LDCRC的分类准确率.从实验结果不难发现,当λ和γ较小时,LDCRC可以获得较好的分类准确率,这一发现可以提高LDCRC的实用性.在AR、ORL、PIE29和PolyU等4个数据集上,LDCRC的分类准确率较高,在γ较小的情况下,LDCRC对λ并不敏感.对IMM和LFW这2个数据集,LDCRC的分类准确率受参数影响的波动较大,这说明IMM和LFW这2个数据集的结构较为复杂,导致基于表示理论的分类方法在研究这类数据集的分类准确率不高.

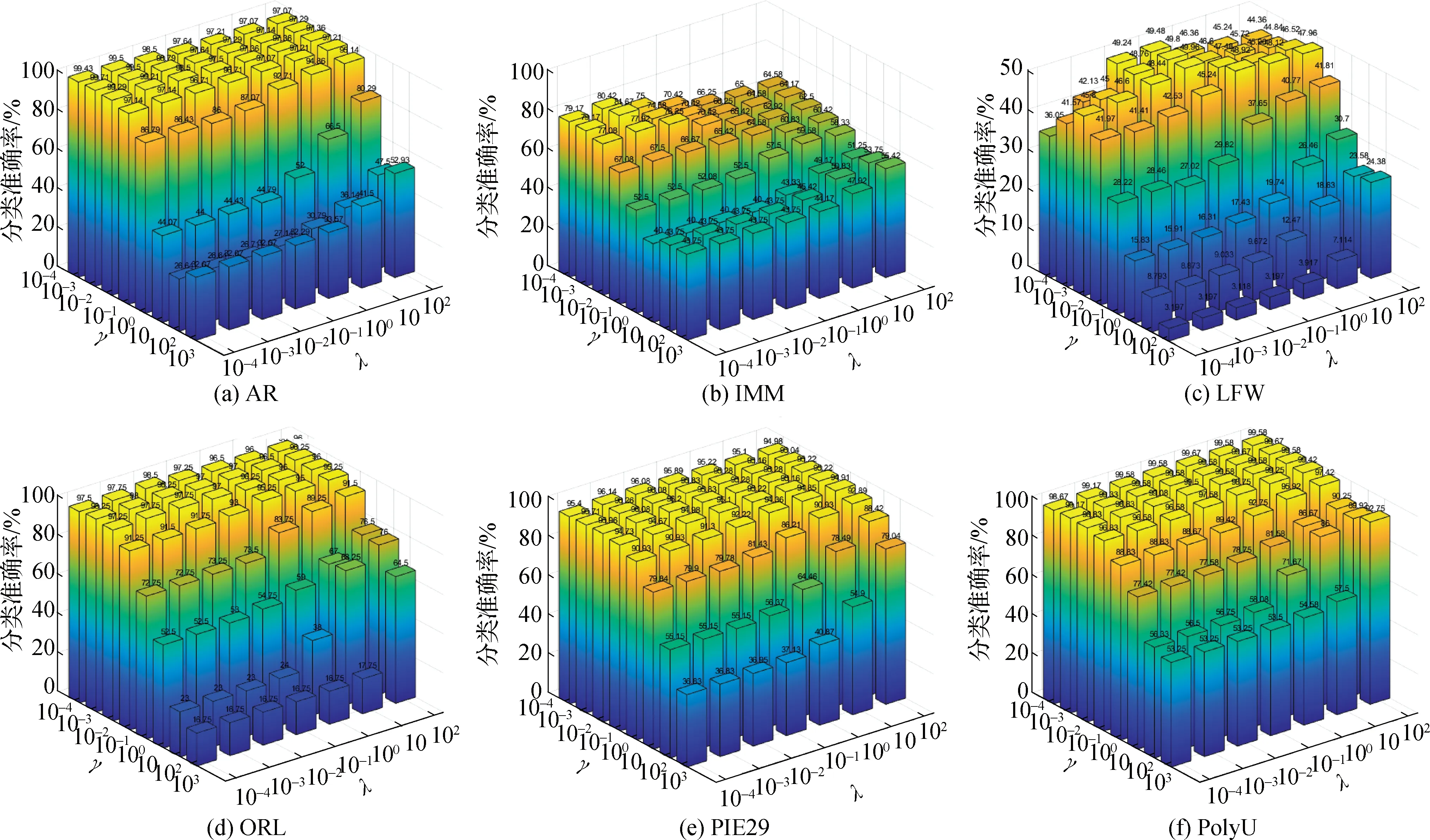
图2 不同γ和λ下的分类准确率Fig.2 Classification accuracies under different γ and λ

4 结 论

本文提出LDCRC,通过定义判别信息惩罚项以增强表示系数的判别能力,并定义局部系数强化项以增强近邻样本的协同表示能力.在6个标准的图像数据集上的实验表明LDCRC具有判别能力和协同表示能力,可以提高CRC等方法的分类准确率.LDCRC在复杂数据集,如IMM和LFW上的分类准确率不高,将在今后的研究中给出更适合复杂数据集分类的方法.LDCRC存在着参数选择问题,利用启发式搜索方法,如遗传算法等进行正则参数的选取将在今后的研究中给出.