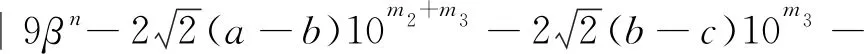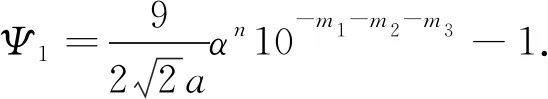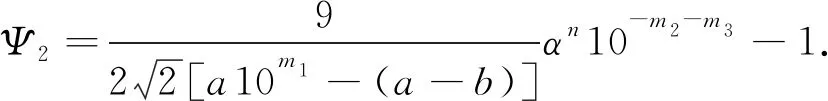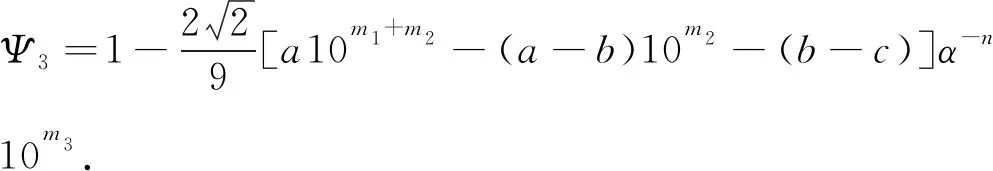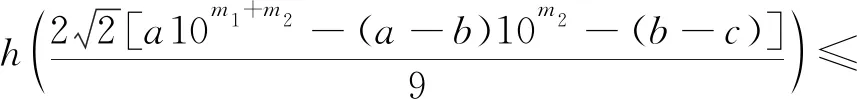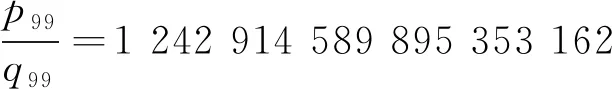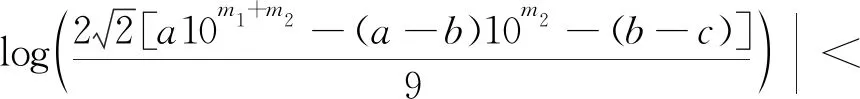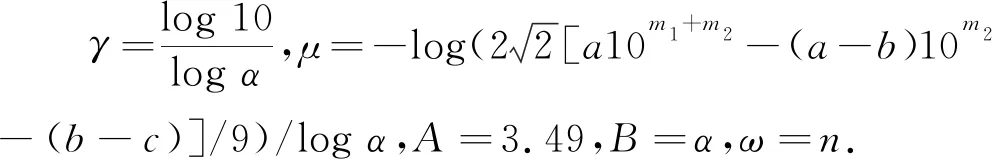可表为3个纯位数串联的Pell数
2023-06-13周建华瞿云云朱山山曾吉文
周建华,瞿云云*,朱山山,曾吉文
(1.贵州师范大学数学科学学院,贵州 贵安新区 550025;2.厦门大学数学科学学院,福建 厦门 361005)
1 引言及主要结果

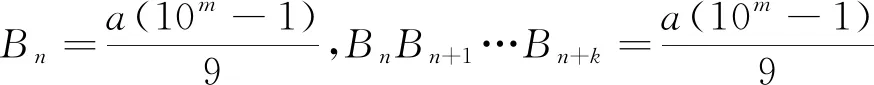
本文使用代数数对数的线性形式以及Baker-Davenport约减方法,找到了所有可表为3个纯位数串联的Pell数,即得到下面的结果:
定理1丢番图方程
(1)
仅有正整数解(n,Pn)∈{(7,169),(8,408),(9,985)},其中a,b,c∈{0,1,…,9},a>0,a≠b,b≠c且mi∈Z+(i=1,2,3).
2 预备知识
αn-2≤Pn≤αn-1.
(2)
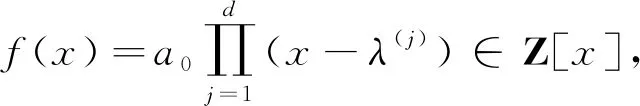
h(λ+η)≤h(λ)+h(η)+log 2,
h(λη±1)≤h(λ)+h(η),h(λm)≤|m|h(λ),
其中λ和η都是代数数,m∈Z.
最后,介绍以下3个引理.∀x∈R,设‖x‖=min{|x-n|:n∈Z}表示从x到最近整数n的距离.
引理1[11-12]设Κ为一个dΚ次实代数数域,且λ1,λ2,…,λt∈Κ为正的实代数数,b1,b2,…,bt为有理整数.设Ψ=λ1b1λ2b2…λtbt-1.如果Ψ≠0,则有
(1+logB)A1A2…At),
其中B≥max{|b1|,|b2|,…,|bt|}且Aj≥max{dΚh(λj),|logλj|,0.16}(j=1,2,…,t).
如下的引理2是文献[13]的一个变形.
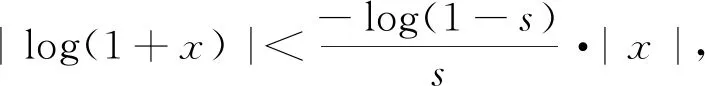
3 定理1的证明
定理1的证明由方程(1)得
(3)
从而有
(b-c)10m3-c].
(4)
考虑当a,b,c∈{0,1,…,9},a>0,a≠b和b≠c时,使用程序找到了方程(1)在n∈[1,1 000]范围内的所有的正整数解如定理所示.现在,假设n>1 000,下证在该范围内方程(1)无其他正整数解.
结合不等式(2)和方程(1)可得10m1+m2+m3-1 m2+m3)+2. (5) 接下来,分3个步骤讨论方程(4). 步骤1方程(4)可写为 两边取绝对值有 10m2+m3<29×10m2+m3. (6) h(λ2)=h(α)=(logα)/2<0.45, h(λ3)=h(10)=log 10<2.31. 因此,可取A1=6.48≥max{dΚh(λ1),|logλ1|,0.16},A2=0.9和A3=4.62.因为m1+m2+m3 11×10-m1>|Ψ1|>exp[-2.62× 1013(1+logn)], 两边取对数,可得 m1log 10<2.62×1013(1+logn)+log 11. (7) 步骤2重写方程(4)为 两边取绝对值有 9.9×10m3<29×10m3. (8) h(a10m1)+h(a-b)+log 2≤h(9)+ log 2<8.33+m1log 10. 因此,可取A1=16.66+2m1log 10,A2=0.9,A3=4.62和B=max{|b1|,|b2|,|b3|}=n.由不等式(8)和引理1,可得 11×10-m2>|Ψ2|>exp[-4.04× 1012(1+logn)(16.66+2m1log 10)], 两边取对数,可得 m2log 10<4.04×1012(1+logn)(16.66+ 2m1log 10)+log 11. (9) 步骤3再重写方程(4)得 两边取绝对值有 两边同时除以9αn,得到 (10) h(λ1)= (m1+m2)h(10)+h(a-b)+m2h(10)+ h(b-c)+2log 2<11.22+m1log 10+ 2m2log 10, 因此,可取A1=22.44+2m1log 10+4m2log 10,A2=0.9,A3=4.62和B=max{|b1|,|b2|,|b3|}=n.由不等式(10)和引理1,可得 3α-n>|Ψ3|>exp[-4.04×1012(1+ logn)(22.44+2m1log 10+4m2log 10)], 两边取对数,可得 nlogα-log 3<4.04×1012(1+logn)(22.44+ 2m1log 10+4m2log 10). (11) 结合不等式(7),(9)和(11)可得, nlogα<3.43×1039[1+(logn)3]+1.03× 1040[logn+(logn)2], 计算得n<4.66×1045,由式(5)左端不等式知m1+m2+m3<1.79×1045,故有m1+m2+m3 然后,使用引理2减少n的上界.设 不等式两边同时除以logα得 0< 966 906 984 107 996 622 451 342 711 342· (475 757 483 963 622 834 701 712 499 334 135 536 483 955 779 839)-1, 且q99>6M,对所有的a∈{1,2,…,9}计算可得最小的ε=‖μq99‖-M‖γq99‖>0.109 100 11,由引理2得,ω=m1<49.878,故得m1≤49.若m1≤2,则也满足m1≤49.将m1≤49代入不等式(9)和(11)得 nlogα<1.59×1028[1+(logn)2]+3.17× 1028logn, 计算可得n<1.01×1032且m2+m3 φ2=(m2+m3)log 10-nlogα- 不等式两边同时除以logα得 429 512·(1 902 082 001 674 088 766 069 917 116 107 203 431)-1, 且q79>6M,对所有的m1≤49,a,b∈{0,1,…,9},a>0且a≠b时,可得最小的ε=‖μq79‖-M‖γq79‖>0.000 184 57,由引理2得,ω=m2<41.252,故得m2≤41.若m2≤2,则也满足m2≤41.将m1≤49和m2≤41代入不等式(11)可得 nlogα<2.53×1015(1+logn), 计算得n<1.16×1017且m3 φ3=m3log 10-nlogα+ 3.07×α-n, 不等式两边同时除以logα得 且q48>6M,对所有的m1≤49,m2≤41,a,b,c∈{0,1,…,9},a>0且a≠b,b≠c时,可得到最小的正数ε=‖μq48‖-M‖γq48‖>2.426 745 39×10-7,由引理2可得,ω=n<75.502,故得n≤75.但是,当(m1,m2,a,b,c)∈{(1,19,6,3,7),(1,23,1,0,9),(7,16,5,1,2),(13,2,6,8,3)}时,出现ε≤0的情况.因此,对相同的M,再取γ的第49个渐进分数为 且q49>6M.此时,可得最小的正数ε=‖μq49‖-M‖γq49‖>0.188 343 11,且ω=n<60.561,故得n≤60.综上所述,得到n≤75,这与假设n>1 000矛盾. 综上,定理得证.