基于核主成分分析的GSA-SVM木材单板缺陷识别研究

贺春光 李璐芳 高峰 袁云梅 高凡 丁安宁 多化琼

摘要：為支持向量机能够准确识别木材单板表面缺陷，以提高木材单板质量，提出高效准确的单板缺陷核主成分分析（KPCA）的引力搜索算法（GSA）-支持向量机（SVM）识别模型。考虑到图像特征数据间的冗余影响，采用KPCA方法对原始特征数据降维，并通过GSA优化SVM的惩罚因子C和核参数g，建立KPCA- GSA-SVM 木材单板缺陷识别模型。基于颜色、纹理、形状3方面的特征以活节、死节、裂纹为研究对象的样本原始数据集，选取8个主要特征（1个颜色特征、1个纹理特征和6个形状特征）作为木材单板识别依据，对木材单板识别模型进行学习训练及预测分析，并与传统粒子群参数优化算法（PSO）构成的KPCA- PSO -SVM识别模型进行识别效果对比。结果表明，基于KPCA-GSA-SVM 木材单板识别模型对于活节、死节、裂纹的识别率达到100%、96.78%、100%，较KPCA- PSO -SVM识别模型分别高出21.62%、0.63%、7.41%，且整体耗费时间缩短7.26 s，由此看出预测识别率、识别速度、稳定性高于前者。研究结论从新的角度对单板缺陷进行识别，有助于木材单板缺陷的识别发展。

关键词：单板缺陷，引力搜索算法，支持向量机，核主成分分析，识别模型

中图分类号：S784文献标识码：A文章编号：1006-8023（2023）02-0091-09

Study on GSA-SVM Wood Veneer Defect Identification Based

on Kernel Principal Component Analysis

HE Chunguang1， LI Lufang1， GAO Feng2， YUAN Yunmei3， GAO Fan1， DING Anning1， DUO Huaqiong1*

（1. College of Materials Science and Art Design， Inner Mongolia Agricultural University， Hohhot 010018， China; 2. Vocational

and Technical College， Inner Mongolia Agricultural University， Baotou 014109， China; 3. School of

Information Engineering， Shanxi College of Applied Science and Technology， Taiyuan 030000， China）

Abstract：In order for the support vector machine to accurately identify the surface defects of wood veneer and improve the quality of wood veneer， an efficient and accurate recognition model of kernel principal component analysis （KPCA） gravity search algorithm-support vector machine （GSA-SVM） for veneer defects was proposed. Considering the redundant effect between image feature data， KPCA method was used to reduce the dimension of original feature data， and GSA optimized the penalty factor C and kernel parameter g of support vector machine （SVM） to establish KPCA-GSA-SVM wood veneer defect recognition model. Based on the three features of color， texture and shape， the raw data set of samples with live knots， dead knots and cracks as the research objects， 8 main features （1 color feature， 1 texture feature and 6 shape features） were selected as the basis for wood veneer recognition. The wood veneer identification model was learned， trained， predicted and analyzed， and the identification effect was compared with the KPCA-PSO-SVM identification model composed of the traditional particle swarm parameter optimization algorithm （PSO）. The results showed that the recognition rate of live knots， dead knots and cracks of the wood veneer recognition model based on KPCA-GSA-SVM was 100%， 96.78% and 100%， which were 21.62%， 0.63% and 7.41% higher than that of KPCA-PSO-SVM， and the overall time was shortened by 7.26 s， it can be seen that the prediction recognition rate， recognition speed and stability were higher than the former. The research conclusions identify the veneer defects from a new perspective， which is helpful for the identification and development of wood veneer defects.

Keywords：Veneer defects; gravity search algorithm; support vector machine; kernel principal component analysis; recognition model

收稿日期：2022-06-02

基金项目：内蒙古自治区重点研发和成果转化计划项目（2022YFDZ0031）

第一作者简介：贺春光，博士研究生，讲师。研究方向为图像处理在木材科学中的应用。Email： hcghcg008@163.com

*通信作者：多化琼，博士，教授。研究方向为木材科学与技术。Email： duohuaqiong@163.com

引文格式：贺春光，李璐芳，高峰，等.基于核主成分分析的GSA-SVM木材单板缺陷识别研究[J].森林工程，2023，39（2）：91-99.

HE C G， LI L F， GAO F， et al. Study on GSA-SVM wood veneer defect identification based on kernel principal component analysis[J].Forest Engineering， 2023， 39（2）：91-99.

0引言

近些年，随着单板行业的不断发展，人们开始逐渐提高单板质量要求，生产企业需要在保证使用性能的基础上，确保单板具有良好的表面质量。但在实际操作中，单板表面缺陷的产生往往是不可避免的。其中活节、死节、裂纹作为常见且具有代表性的单板表面缺陷，不仅破坏木材均匀性，影响成材表现，还降低木材某些力学性质，加大木材的加工难度，伤害木材单板质量，是影响装饰质量及单板的商品价值和使用价值的主要影响因素。因此有效地进行木材单板表面缺陷的自动识别显得尤为重要。

随着现代计算机技术的不断发展，基于数字图像处理技术的木材单板缺陷识别与检测研究方法理论已日趋成熟[1-2]。目前，在木材识别方法中应用较为广泛的方法有支持向量机、BP（Back Propagation）神经网络与深度神经网络等。马旭等[3]基于支持向量机的核函数理论，用于木材缺陷分类，并通过大量实验得出多项式核函数与其他识别方法对比，识别精度最高且误差较小。Zhang等[4]、郭慧等[5]、Ji等[6]、罗微等[7]以木材缺陷为研究对象提取图像纹理特征，采用BP神经网络作为分类器对木材缺陷进行识别，识别率可达93%，结果表明，BP神经网络可以有效提高分类器的性能和识别准确率。然而目前很多木材单板的识别方法存在一定的局限性，如Kaur等[8]、Zhang等[9]方法效率与应用效果受识别参数影响较大，宋月婵等[10]、Cuong-le等[11]优化算法，虽能在一定程度上提高SVM木材单板缺陷的识别效率，但对于不同的缺陷其实际效果有所降低，且模型本身易陷入局部最优化。

针对以上问题，本研究以单板缺陷中活节、死节、裂纹为例，利用核主成分分析（Kernel Principal Component Analysis，KPCA）进行特征降维选取最佳的特征数据，利用引力搜索算法（Gravity Search Algorithm，GSA）对支持向量机（Support Vector Machines，SVM）的惩罚因子C和核参数g进行寻优，建立基于 KPCA-GSA-SVM 的木材单板缺陷识别模型，以期提高木材单板缺陷识别的准确性[12]。

1KPCA-GSA-SVM理论基础

1.1核主成分分析（KPCA）

KPCA是对传统主成分分析算法的非线性扩展线性降维方法，其目标是保留较多的原数据点特性，同时能够挖掘到数据集中蕴含的非线性信息[13-14]。其核主成分分析的主要步骤如下。

将获取的木材单板缺陷原始数据在空间R进行非线性映射

φ：R→H。（1）

式中：R为原始数据空间；H为特征空间，其中通过映射原始数据xi（i=1，2，…，N）在特征空间的像为φ（Xi），则φ（Xi）的协方差矩阵

C=1N-1∑Ni=1φ（Xi）φ（Xi）T=

1N-1（φ（X1），…，φ（XN））φ（X1）Tφ（XN）T 。（2）

式中：当 XT=（φ（X1），…，φ（XN）），则存在C=1N-1XTX。但由于φ（X）函数未知，所以需要引入核函数（K）

K=XXT=φ（X1）Tφ（XN）T（φ（X1），…，φ（XN））=

k（X1，X1）…k（XN，X1）k（XN，X1）…k（XN，XN）。（3）

核函数中心化Kc处理得到

Kc=K-lNK-KlN+lNKlN 。（4）

式中：lN为N×N的矩阵，每一个元素都为1/N。而核矩阵Kc的特征值与特征向量关系式为

（XXT）u=λu 。（5）

式中：u为代表Kc的特征向量；λ为Kc的特征值。将求得的特征值進行归一化处理，利用特征值的累积贡献率进行选取

∑nj=1λj/∑Ni=1λi≥E 。（6）

式中：∑nj=1λj代表前n个特征值累计在整个特征值综合的比值大于阈值E，通常为使保证数据降维后仍能保留足够特征信息。

1.2支持向量机

支持向量机[7，16-17]是一种常见的机器学习识别方法，基本原理是：在线性可分条件下，构造最优超平面，在最初空间将其完全分开，对于非线性利用核公式将低纬度非线性问题转化为高纬度线性问题。作为二分类问题，支持向量机对于解决多分类问题存在一定的障碍，因此，研究人员在已有基础上提出来多分类支持向量机方法。通过组合二分类的方法来进一步实现多分类识别问题。但其算法性能又与惩罚因子C和核参数g取值有非常紧密联系，如果惩罚因子C和核参数g选择不当，算法性能会很差，SVM针对多分类对象的具体步骤见文献[18-19]。

1.3引力搜索机

引力搜索算法[20-21]是基于万有引力定理，指引粒子更新位置从低质量粒子转向高质量粒子发展，其中粒子位置为最优解，通过不断更新换代寻找最优解的算法，其中具体的过程如下。初始化粒子位置，其中系统包含N个粒子

Xi=（x1i，…，xdi，…，xNi），i=1，2，…， N。（7）

式中：xdi表示第i个粒子的在d维中的位置。但不同的粒子之间存在着引力作用，且不同的迭代引力的作用也会发生变化

Fdij（t）=G（t）Mpi（t）×Maj（t）Rij（t）+ε（xdj（t）-xdi（t））。（8）

式中：Maj（t）为主动粒子j的惯性质量；Mpi（t）为被动粒子的i的惯性质量；Rij（t）为粒子间的欧式距离；ε为常数；G（t）则作为t次迭代的引力常数

G（t）=G0e-αtT 。（9）

式中：G0和α是常数；T为迭代总数。在引力作用下每个粒子的速度与作用发生变化

vdi（t）=randi×vdi（t）+αdi（t）

xdj（t）=xdj（t）+vdi（t）。（10）

式中：randi表示0，1中的随机数，提高算法中的随机性；αdi（t）表示在第t次迭代中i的加速度

αdi（t）=Fdi（t）Mi（t） 。（11）

式中：Fdi（t）代表在d维上粒子i受其他粒子的作用力合力；Mi（t）代表粒子的惯性质量，具体见式 （12）—式（14）

Fdi（t）=∑Nj=1，j=1randiFdij（t） 。（12）

Mi（t）=mi（t）∑Nj=1mj（t）。（13）

mi（t）=fiti（t）-worst（t）best（t）-worst（t） 。（14）

式中：mi（t）表示第i个粒子的重力；fit，i（t）代表在第t次迭代时粒子的适应度值；best（t）为最佳适应度值worst（t）为最差适应度值。

1.4KPCA-GSA-SVM模型建立

本研究利用核主成分分析对GSA-SVM模型参数进行优化识别参数优化，提高识别效率，增加识别效果，具体过程如下。

步骤 1：提取图像特征，构成木材单板缺陷图像特征集。

步骤 2：对数据集进行标准化处理，可以得到输入样本，求核矩阵K，使用核函数来实现将原始数据由数据空间映射到特征空间，计算在高维空间中对映射的非线性数据进行中心化后的核矩阵。

步骤 3：计算矩阵Kc的特征值以及对应的特征向量，进行单位化处理。并计算特征值求出贡献率，根据累计贡献率求域值p（95%），如果t>p，则选取前t个主分量，作为降维后的数据，并分为训练集与测试集。

步骤 4：初始化所有粒子的位置与速度，设置最大迭代数与相关参数。

步骤 5：建立粒子的适应度函数，利用最小化、最大化公式计算最佳适应度值bbest（t）和最差适应度值worst（t），根据不同适应值，更新确定惯性质量Mi（t）、mi（t）。计算粒子的加速度，确定粒子所受合外力。

步骤 6：根据确定的加速度，利用公式计算粒子的速度和位置。

步骤 7：之后根据所求的全局最优解gbest（t）所需要达到预设精度或最大迭代次数进行步骤4循环迭代，直到算法终止，将求出最优参数带入SVM模型中，进行图像识别。

为进一步详细表述上述流程，现将其构成具体线性流程图，如图1所示。

2基于KPCA-GSA-SVM的木材单板缺陷识别

2.1特征选取

2.1.1图像预处理

实验使用戴尔台式计算机，Windows7操作系统，C++编辑器与MATLAB软件运行，利用佳能照相机进行相片采集。采集木材单板缺陷图像210张（死节、活节与裂纹各70张），选取120张作为数据集，90作为实验集，原始缺陷图像大小为256×256像素。

但在实际生产采集过程中由于受木屑、灰尘、照度不足和光线不均等因素影响，部分采集的图像质量效果差，部分信息模糊，构成识别结果与实际期盼差距较大。为解决上述问题，本研究通过对木材死节、活节与裂纹图像进行自适应高斯滤波[22-23]与自适应伽马校正[24-25]相结合方式来达到提高图像质量，消除图像中沉郁的信息，恢复与增强有关信息的可检测性的效果[26]，图2为其中3张原始图的预处理结果。

2.1.2图像特征提取

木材缺陷识别是基于多种信息的提取与检测，图像信息的提取也是图像识别的重要步骤，通过对木材缺陷图像的颜色、纹理、形状和轮廓等多方面信息的提取，构成每张图像独有的非图像数字化表达，并以此为基础建立了许多基于数字图像技术的木材缺陷特征提取方法，为更加完善图像信息的提取，促进图像识别技术的发展，本研究采用颜色、纹理和形状3方面进行特征的提取，通过对颜色通道R、G、B进行三阶矩的计算得出颜色特征[27-29]，并利用Gabor小波變化[30-31]的纹理特征选取方向为π/7、π/8、π/9、π/10、π/11的图像进行均值、对比度、方差特征求解得到图像纹理特征，最后根据Hu不变矩[32-33]对平移、缩放、镜像和旋转都不敏感的7个二维不变矩的得出形状特征，最终构成对木材不同缺陷图像的特征集。

2.1.3特征数据KPCA 处理

为减少特征数据之间的冗余，达到预期识别效果，对已有的1个图像颜色、1个纹理特征和6个形状特征进行特征降维，选择合适的特征作为最终的识别参数。其中为减少数据之间较大的差距，需要对特征集进行无量纲化处理，将所有特征数据标准化，所有数据确定在0到1之内，再根据核函数求取核矩阵K确定函数的特征值与特征向量，并将特征值进行方差贡献率计算求出占比最高的特征值，其中图像特征方差贡献率表示单个特征在图像特征集中影响力的大小，具体数据如图3所示。

由图3可知，在特征降维过程中，特征值占比大小，对总体特征集的影响力较大。因此，在特征识别过程中一般选取累计贡献率达到95%以上的数值作为主要识别数值用于图像的识别研究。本实验基于上述原则与图像信息，选取前8位作为识别特征用于研究，其中选取的特征分别为颜色特征的颜色矩、纹理特征的π/10的方差值，以及形状特征的6个二维不变矩，表示特征集易受到图像的颜色分布情况、在π/10纹理方向的方差以及在Hu不变矩平移、缩放、镜像和旋转等不敏感的6个二维不变矩的影响，部分具体结果见表1。

2.2单板缺陷识别

将KPCA提取到的8个主成分作为GSA-SVM预测模型的输入向量，在Matlab 软件平台上编写相应程序代码，建立木材缺陷识别的KPCA-GSA-SVM 模型。为验证 KPCA-GSA-SVM 预测模型的优越性，将其与KPCA-PSO-SVM[34]模型作对比，模型相关参数是按照相关论文研究成果[21，32，34]及实际测试合理设定，见表2。

将表2中的参数带入不同的识别模型中，由图4可知，通过粒子群算法可以得到最佳适应度与平均适应度的惩罚参数C和核函数参数g的最优解，分别为7.64、0.75，粒子群算法平均适应度整体较低，其惩罚参数C相对更高。引力搜索算法可以得出最佳适应度与平均适应度的惩罚参数C和核函数参数g，

最优解分别为4.88、1.45，相比较粒子群算法该算法的平均适应度与最佳适应度整体较低，且最佳适应度与平均适应度差值较大，迭代次数更少，因此整体运行速度更快，其惩罚参数C也相对更高，将得到的识别参数带入KPCA-SVM分类模型，得出测试集训练结果，如图5所示。

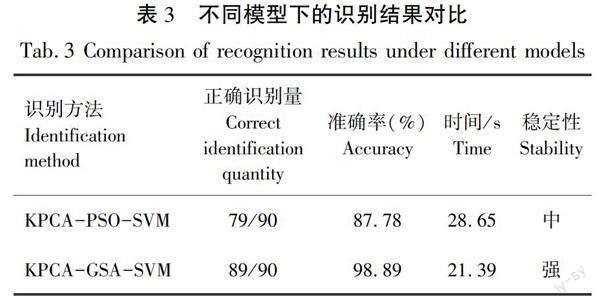
由表3可知，总体粒子群算法与引力搜索算法的识别率分别为 87.78%、98.89%，耗费时间分别为28.65、21.39 s，由此可知，引力搜索算法比粒子群算法整体识别率较高，运行速度更佳，具有更强的稳定性、泛化能力和学习能力，适应范围较广。

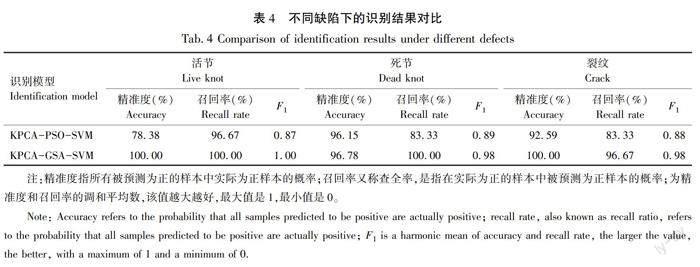
但上述识别图像是面对整体特征进行识别求解，为进一步对比研究活节、死节、裂纹3种不同缺陷分别在KPCA-PSO-SVM、KPCA-GSA-SVM优化方法下的识别效果，将上述识别结果进行拆分得出不同缺陷在不同优化方法下的识别结果，见表4。由表4可知，对于活节、死节、裂纹的识别率达到100%、96.78%、100%，KPCA-GSA-SVM相对于KPCA-PSO-SVM高出21.62%、0.63%、7.41%。同时在召回率与F1等评价指标相比，KPCA-GSA-SVM模型也远高于KPCA-PSO-SVM模型，且整体耗费时间缩短7.26 s，由此可知本研究基于KPCA-GSA-SVM算法在木材单板缺陷图像的识别效率与模型稳定性相对于KPCA-PSO-SVM算法有所提升。

3结论

随着现代计算机技术的高速发展，计算机数字图像处理技术已成为当前追逐的热点，并广泛应用在木材单板领域中。数字图像技术所具备的线性好、精度高和灵活性强等优势，为木材单板识别提供了新的发展手段。本研究基于传统支持向量机，提出基于核主成分分析的GSA-SVM识别模型，对木材单板的不同缺陷进行识别研究。

1）本研究建立了KPCA-GSA-SVM单板缺陷识别模型，利用KPCA方法对原始数据进行主成分特征提取，减少数据间的量化信息，对模型数据进行降维，提高算法运行效率。并在此基础上引入GSA搜索算法对SVM的惩罚因子C和核参数g进行寻优，GSA算法比PSO算法具备参数更少，搜算算法更加广泛等优势，在一定程度上提高了模型的识别效率与运行速率。与KPCA-PSO-SVM 模型比较，KPCA-CSA-SVM 模型的判别准确率和运行速度更佳，具有更强的稳定性、泛化能力和学习能力[35-39]。

2）但由于客观条件的限制，本研究所收集的数据有限，且主要针对杨木、樟子松的2类缺陷完成了识别工作，当识别对象为样本库外树种的缺陷可能存准确率不高的情況，对于不同树种的缺陷可能识别效果不好，因此，在今后的研究工作中，还需要进行更为完善的研究，有必要收集更加丰富的实测数据资料，以提供更加可靠的判别信息，增强模型的适用性[40]。

【参考文献】

[1]尚宇辉.大数据与数字图像处理技术的应用[J].集成电路应用，2021，38（10）：90-91.

SHANG Y H. Application of big data and digital image processing technology[J]. Application of IC， 2021， 38（10）： 90-91.

[2]吴少霜，赵纯，朱亚男，等.数字图像处理技术在果蔬分级检测中的应用[J].福建农机，2021（3）：30-36.

WU S S， ZHAO C， ZHU Y N， et al. Application of digital image processing technology in fruit and vegetable grading detection[J]. Fujian Agricultural Machinery， 2021（3）： 30-36.

[3]马旭，刘应安，业宁，等.基于核PCA与SVM算法的木材缺陷识别[J].常州大学学报（自然科学版），2017，29（3）：60-68.

MA X， LIU Y A， YE N， et al. Application of KPCA and SVM to wood defect recognition[J]. Journal of Changzhou University （Natural Science Edition）， 2017， 29（3）： 60-68.

[4]ZHANG Y X， ZHAO Y Q， LIU Y， et al. Identification of wood defects based on LBP features[C]//2016 35th Chinese Control Conference （CCC）. July 27-29， 2016， Chengdu， China. IEEE， 2016： 4202-4205.

[5]郭慧，王霄，刘传泽，等.基于灰度共生矩阵和分层聚类的刨花板表面图像缺陷提取方法[J].林业科学，2018，54（11）：111-120.

GUO H， WANG X， LIU C Z， et al. Research on defect extraction of particleboard surface images based on gray level co-occurrence matrix and hierarchical clustering[J]. Scientia Silvae Sinicae， 2018， 54（11）： 111-120.

[6]JI X Y， GUO H， HU M H. Features extraction and classification of wood defect based on hu invariant moment and wavelet moment and BP neural network[C]//Proceedings of the 12th International Symposium on Visual Information Communication and Interaction. Shanghai China. New York， NY， USA： ACM， 2019： 37：1-5.

[7]羅微，孙丽萍.利用局部二值模式和方向梯度直方图融合特征对木材缺陷的支持向量机学习分类[J].东北林业大学学报，2019，47（6）：70-73.

LUO W， SUN L P. Wood defect detection and classification by fusion feature and support vector machine[J]. Journal of Northeast Forestry University， 2019， 47（6）： 70-73.

[8]KAUR I， AGGARWAL G， VERMA A. Detection and classification of disease affected region of plant leaves using image processing technique[J]. Indian Journal of Science and Technology， 2016， 9（48）： 1-13.

[9]ZHANG Z H， LUO Y C， DENG X D， et al. Digital image technology based on PCA and SVM for detection and recognition of foreign bodies in lyophilized powder[J]. Technology and Health Care： Official Journal of the European Society for Engineering and Medicine， 2020， 28（S1）： 197-205.

[10]宋月婵，刘光萍.基于KPCA-SVM的预测模型在铀矿堆浸中的应用[J].江西科学，2015，33（1）：106-111.

SONG Y C， LIU G P. The application of heap leaching of uranium based on KPCA-SVM[J]. Jiangxi Science， 2015， 33（1）： 106-111.

[11]CUONG-LE T， NGHIA-NGUYEN T， KHATIR S， et al. An efficient approach for damage identification based on improved machine learning using PSO-SVM[J]. Engineering With Computers， 2022， 38（4）： 3069-3084.

[12]ROSSO M M， CUCUZZA R， DI TRAPANI F， et al. Nonpenalty machine learning constraint handling using PSO-SVM for structural optimization[J]. Advances in Civil Engineering， 2021， 2021： 1-17.

[13]刘波，宁芊.基于特征融合和KPCA＿GA-SVM的滚动轴承故障诊断[J].现代计算机（专业版），2019（11）：32-38.

LIU B， NING Q. Mechanical bearing fault diagnosis based on feature fusion and KPCA＿GA-SVM[J]. Modern Computer， 2019（11）： 32-38.

[14]KUANG F， ZHANG S， XU W. A novel hybrid KPCA and SVM with GA model for intrusion detection[J]. Applied Soft Computing， 2014， 18： 178-184.

[15]谭念，孙一丹，王学顺，等.基于主成分分析和支持向量机的木材近红外光谱树种识别研究[J].光谱学与光谱分析，2017，37（11）：3370-3374.

TAN N， SUN Y D， WANG X S， et al. Research on near infrared spectrum with principal component analysis and support vector machine for timber identification[J]. Spectroscopy and Spectral Analysis， 2017， 37（11）： 3370-3374.

[16]王学顺，孙一丹，黄安民.木材红外光谱的树种识别研究[J].森林工程，2015，31（6）：65-70.

WANG X S， SUN Y D， HUANG A M. Research on infrared spectrum for timber species identification[J]. Forest Engineering， 2015， 31（6）： 65-70.

[17]张冬妍，张春妍，尹文芳.基于KPCA和PSO-SVM的木材干燥过程在线优化建模研究[J].安徽农业科学，2014，42（7）：1993-1996.

ZHANG D Y， ZHANG C Y， YIN W F. Optimized online modeling of timber drying process using kernal principal component analysis and PSO-SVM[J]. Journal of Anhui Agricultural Sciences， 2014， 42（7）： 1993-1996.

[18]吴啸天.基于多特征提取和SVM分类器的木材显微识别[J].陕西林业科技，2017（5）：11-14.

WU X T. Wood microscopic recognition based on feature extraction and SVM classifiers[J]. Shaanxi Forest Science and Technology， 2017（5）： 11-14.

[19]盛剑桥，方圆，张亮，等.粒子群算法优化SVM的无线网络安全状态检测方法[J].自动化技术与应用，2022，41（12）：55-58.

SHENG J Q， FANG Y， ZHANG L， et al. Particle swarm optimization SVM wireless network security state detection method[J]. Techniques of Automation and Applications， 2022， 41（12）： 55-58.

[20]戴娟，顾斌杰，潘丰.基于引力搜索算法的SVM参数优化及应用[J].江南大学学报（自然科学版），2013，12（2）：127-131.

DAI J， GU B J， PAN F. Parameter optimization and application of SVM based on gravitational search algorithm[J]. Journal of Jiangnan University （Natural Science Edition）， 2013， 12（2）： 127-131.

[21]龔安，吕倩，胡长军，等.基于混沌万有引力搜索算法的SVM参数优化及应用[J].计算机科学，2015，42（4）：240-243.

GONG A， LYU Q， HU C J， et al. Parameter optimization and application of SVM based on chaos gravitational search algorithm[J]. Computer Science， 2015， 42（4）： 240-243.

[22]李健，丁小奇，陈光，等.基于改进高斯滤波算法的叶片图像去噪方法[J].南方农业学报，2019，50（6）：1385-1391.

LI J， DING X Q， CHEN G， et al. Blade image denoising method based on improved Gauss filtering algorithm[J]. Journal of Southern Agriculture， 2019， 50（6）： 1385-1391.

[23]王海菊，谭常玉，王坤林，等.自适应高斯滤波图像去噪算法[J].福建电脑，2017，33（11）：5-6.

WANG H J， TAN C Y， WANG K L， et al. Adaptive Gaussian filter image denoising algorithm[J]. Fujian Computer， 2017， 33（11）： 5-6.

[24]李灿林，刘金华，张卫正，等.一种非均匀照明彩色图像自适应校正方法[J].科学技术与工程，2021，21（10）：4133-4140.

LI C L， LIU J H， ZHANG W Z， et al. An adaptive method for color image correction with non-uniform illumination[J]. Science Technology and Engineering， 2021， 21（10）： 4133-4140.

[25]KANSAL S， TRIPATHI R K. Adaptive gamma correction for contrast enhancement of remote sensing images[J]. Multimedia Tools and Applications， 2019， 78（18）： 25241-25258.

[26]KIM Y， KOH Y J， LEE C， et al. Dark image enhancement based onpairwise target contrast and multi-scale detail boosting[C]//2015 IEEE International Conference on Image Processing （ICIP）. September 27-30， 2015， Quebec City， QC， Canada. IEEE， 2015： 1404-1408.

[27]HEMACHANDRAN K. Image retrieval based on color moments[J]. Digital Image Processing， 2012， 4（16）： 910-916.

[28]RAJ R， SUDHAMANI D M V. Retrieval of images using combination of features as color， color moments and hu moments[J]. Advances in Image and Video Processing， 2019， 7（5）： 9-21.

[29] SINGH H， AGRAWAL D. A hybrid content based image retrieval system based onlocal binary pattern （LBP）， color moment （CM） and edges[J]. International Journal of Engineering and Technology， 2017， 9（1）： 45-54.

[30]刘胜昔，程春玲.改进的Gabor小波变换特征提取算法[J].计算机应用研究，2020，37（2）：606-610.

LIU S X， CHENG C L. Feature extraction algorithm based on improved Gabor wavelet transform[J]. Application Research of Computers， 2020， 37（2）： 606-610.

[31]周华平，张晓宇，姚尚军，等.融合FLBP和Gabor小波的图像轮廓提取算法[J].佳木斯大学学报（自然科学版），2021，39（1）：49-52.

ZHOU H P， ZHANG X Y， YAO S J， et al. An image contour extraction algorithm fused FLBP and Gabor wavelet[J]. Journal of Jiamusi University （Natural Science Edition）， 2021， 39（1）： 49-52.

[32]ZHAO J D， WANG X K. Vehicle-logo recognition based on modified HU invariant moments and SVM[J]. Multimedia Tools and Applications， 2019， 78（1）： 75-97.

[33]KONDUSOV D V， SERGEEV A I， KONDUSOVA V B. Comparison of 3D models using hu moment invariants[J]. Russian Engineering Research， 2020， 40（7）： 570-574.

[34]QIAN X， CHEN J P， XIANG L J， et al. A novel hybrid KPCA and SVM with PSO model for identifying debris flow hazard degree： a case study in Southwest China[J]. Environmental Earth Sciences， 2016， 75（11）： 991.

[35]LUO W， SUN L P. An improved binarization algorithm of wood image defect segmentation based on non-uniform background[J]. Journal of Forestry Research， 2019， 30（4）： 1527-1533.

[36]趙乾.基于极限学习机的实木板材缺陷检测算法研究[D].南京：南京林业大学，2018.

ZHAO Q. Research on defect detection algorithm of solid wood board based on extreme learning machine[D]. Nanjing： Nanjing Forestry University， 2018.

[37]XIE Y H， Wang J C. Study on the identification of the wood surface defects based on texture features[J]. Optik-International Journal for Light and Electron Optics， 2015， 126（19）： 2231-2235.

[38]SHI Z H， FENG Y N， ZHAO M H， et al. Normalised gamma transformation-based contrast-limited adaptive histogram equalisation with colour correction for sand-dust image enhancement[J]. IET Image Processing， 2020， 14（4）： 747-756.

[39]WANG L Z， XI J N， CAO Q， et al. The effect of echocardiography based on lipid nano contrast agent on cardiology patients with heart failure and atrial fibrillation[J]. Journal of Nanoscience and Nanotechnology， 2021， 21（2）： 852-858.

[40]尹建新，祁亨年，冯海林，等.一种基于混合纹理特征的木板材表面缺陷检测方法[J].浙江农林大学学报，2011，28（6）：937-942.

YIN J X， QI H N， FENG H L， et al. A method for wood surface defect detection based on mixed texture features[J]. Journal of Zhejiang A & F University， 2011， 28（6）： 937-942.