谈谈换元法在解题中的妙用

林正坤

在解答比较复杂的代数问题时，我们通常会采用换元法来帮助我们理清题目中的数量关系，使问题化难为易、化繁为简，然后顺利获解.运用换元法解题首先要根据问题的特征或数量关系引进新的辅助元来替换原问题中的数、字母、式子等，然后求出新元的值，再将求得的值带回所设的换元式，带入替换关系中，求出原来的未知量或变量，最后对解出的答案进行检验.本文主要介绍换元法在因式分解、解方程以及整式运算中的应用.

一、换元法在因式分解中的妙用

当我们在进行因式分解时，如果一个多项式的项数、字母较多，次数较高或含有代数式乘积的项时，可对多项式中某些相同的部分设辅助元进行代换，让整个题干的因式项数减少或因数次数降低，从而方便解题.

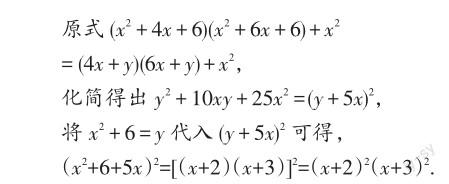
评注：用换元法分解因式时，不必将原式中的元都用新元代换，根据题目需要，引入必要的新元，原式中的变元和新的变元可以一起变形.换元法的本质就是简化多项式.

二、换元法在解方程中的妙用

当我们遇到分式方程、无理方程、高次方程等直接求解比较困难的方程问题时，可考虑运用换元法，把方程中的某个式子看成一个整体，用一个变量去代替它，通过变量代换实现降次、无理式转化为有理式、分式转化为整式的目的，从而使较繁难的问题变为较简易的问题.

评注：如果用开平方的方式解答无理方程，会导致整个方程的次方数过高，使解题过程更加困难.因此我们可以根据题目的要求和代数式的特性，利用换元法把无理方程巧妙地转化为有理方程.

三、換元法在整式运算中的妙用

在整式运算中，对一些较为复杂的题目，直接求解显然不易入手时，同学们可以考虑整体换元.整体换元的关键是要构造元和设元，就是要将已知式中结构相同的某个部分看作一个整体，用一个新的变量去替代它，然后再结合题目形式进行变形求值，从而使问题得以简化.

例3求（1+2+3+…+998）（2+3+4+…+ 999）-（1+2+3+…+999）（2+3+4+…+998）的值.

分析：从整式的整体上来看，我们需要找寻其中的共同点，将这些共同点利用新元进行代替，让整个式子得以简化.通过观察我们可以将第一个式子（1+2+3+…+998）设为x，将（1+2+3+…+999）设为y，然后就可以将其带入后面两个式子中将整式进行简化.

解：设1+2+3+…+998=x；

1+2+3+…+999=y.

将x，y代入原式后可得

x（y-1）-y（x-1）=（xy-x）-（xy-y）

= y-x=999.

评注：本题中每一个代数式都可以用新元替代原有的式子，但是取不同的代数式换元后，运算难度会有所不同，所以我们在利用换元法解题的时候需要仔细观察，寻找规律，找到最合适设置新元的位置代入换算.