有关平面直角坐标系的知识点及考点归纳

顾建明

坐标系与其它数学知识存在不可分割的联系.许多知识在平面直角坐标系中进行研究会更加直观易懂.所以只有牢固掌握了与直角坐标系有关的知识点与考点，才能更好地学习一次函数、反比例函数和二次函数等相关知识.

一、平面直角坐标系相关知识点归纳

1.平面直角坐标系的定义：在平面内画两条互相垂直、原点重合的数轴，就组成平面直角坐标系.水平的数轴称为x轴或横轴，竖直的数轴称为y轴或纵轴，两坐标轴的交点为平面直角坐标系的原点.

2.各个象限内点的特征：右上为第一象限、左上为第二象限、左下为第三象限、右下为第四象限.坐标在四个象限的特点：点P （ x，y）在第一象限则x>0，y>0；在第二象限则x<0，y>0；在第三象限则x<0，y<0；在第四象限则x>0，y<0.

4.点的对称：点P（ m，n），关于x轴的对称点坐标是（ m，-n），关于y轴的对称点坐标是（-m，n），关于原点的对称点坐标是（-m，-n）.

5.平行线：平行于x轴的直线上的点的特征：纵坐标相等，如直线PQ，P（m，n）Q （p，n）；平行于y轴的直线上的点的特征：横坐标相等，如直线PQ、P（m，n）、Q（m，p）.

6.象限角的平分线：第一、三象限角平分线上的点横、纵坐标相等，可记作：P（m，m）；点P （ a，b ）关于第一、三象限坐标轴夹角平分线的对称点坐标是（ b，a ）；第二、四象限角平分线上的点横纵坐标互为相反数，可记作： P（m，-m）；点P （ a，b ）关于第二、四象限坐标轴夹角平分线的对称点坐标是（- b，- a ）.

7.点的平移：在平面直角坐标系中，将点（ x，y）向右平移a個单位长度，可以得到对应点（x + a，y）；向左平移a个单位长度，可以得到对应点（x-a，y）；向上平移b个单位长度，可以得到对应点（x，y+b）；向下平移b个单位长度，可以得到对应点（x，y-b）.

二、平面直角坐标系相关考点归纳

1.求坐标

求点的坐标的方法是过这个点向x轴作垂线，则垂足对应的数就是该点的横坐标；过这个点向y轴作垂线，则垂足对应的数就是该点的纵坐标.确定了一个点的横坐标和纵坐标，就知道这个点的坐标.

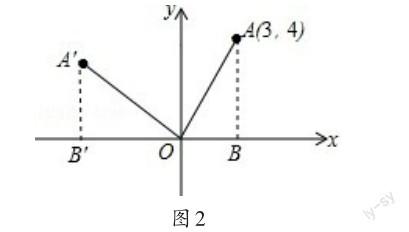
例1如图1，在平面直角坐标系xOy中，已知点A（3，4），将OA绕坐标原点O逆时针旋转90°至OA′，则点A′的坐标是.

例2在平面直角坐标系中，A（-5，0），B（3，0），点C在y轴上，△ABC的面积为12，求点C的坐标.

解：∵点A（-5，0），B（3，0），都在x轴上，

∴AB=8.

∵△ABC的面积为12，点C在y轴上，

解得OC=3，

若点C在y轴的正半轴上，则点C的坐标为（0，3），若点C在y轴的负半轴上，则点C的坐标为（0，-3），

综上所述，点C的坐标为（0，3）或（0，-3）.

2.求象限

在平面直角坐标系中，各象限内点的符号特点是：第一象限内的点，横坐标和纵坐标都为正；第二象限内点的横坐标为负，纵坐标为正；第三象限内点的横坐标和纵坐标都为负；第四象限内点的横坐标为正，纵坐标为负.确定了点横坐标及纵坐标的正负，就确定了象限.

例3若点M（x，y）满足（x+y）2= x2+ y2-2，则点M所在象限是（）.

A.第一象限或第三象限

B.第二象限或第四象限

C.第一象限或第二象限

D.不能确定

解：∵（x+y）2= x2+ y2+2xy，

∴原式可化为xy=-1，

∴x、y异号，

∴点M（x，y）在第二象限或第四象限.

故选B项.

故选B项.

3.求面积

当三角形有一边在x轴上时，则以x轴上的边为底边，其长等于x轴上两个顶点横坐标差的绝对值，此边上的高就等于另一个顶点纵坐标的绝对值；当三角形的一边在y轴上时，则以y轴上的边为底边，其长等于y轴上两个顶点纵坐标差的绝对值，此边上的高就等于另一个顶点横坐标的绝对值.确定了三角形的底边和高就能求出面积.

例5如图3，△ABC的三个顶点坐标分别是A（2，4），B（-2，0），C（3，0），求△ABC的面积.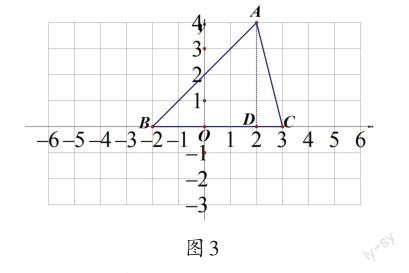

解：过A作AD⊥x轴，垂足为D，

∵A的坐标是（2，4），

∴AD=4，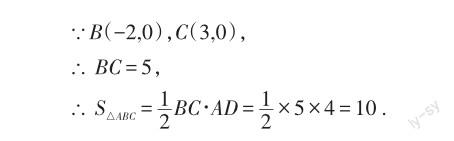

例6如图4，平面直角坐标系中，已知点A（-3，-1），B（1，3），C（2，-3），求三角形ABC的面积.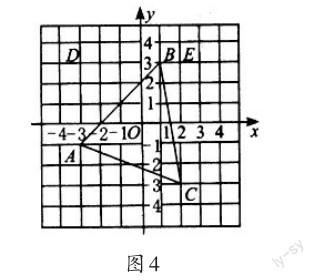

分析：由于三边均不平行于坐标轴，所以我们无法直接求边长，也无法求高，因此得另想办法.根据平面直角坐标系的特点，可以将三角形围在一个梯形或长方形中，这个梯形（长方形）的上下底（长）与其中一个坐标轴平行，高（宽）与另一个坐标轴平行.这样，梯形（长方形）的面积就容易求出，然后再减去围在梯形（长方形）内边缘部分的直角三角形的面积，即可求得原三角形的面积.

解：如图5，过点A、C分别作平行于y轴的直线，与过点B平行于x轴的直线交于点D、E，则四边形ADEC为梯形.