基于贝叶斯理论的多雷达点迹自适应融合方法

江 兵,周传睿,姚 元

(南京电子技术研究所,江苏 南京 210039)

随着干扰、诱饵等电磁对抗手段的广泛应用,单平台雷达已难以满足高质量目标信息保障需要,多站雷达组网进行探测数据融合成为应对日益复杂的电磁环境的必要途径,能提供更精确的目标状态信息、增强预警探测系统的容错能力和自适应能力、提高系统的可靠性和鲁棒性、扩展系统的时空覆盖率[1-2],对提高复杂环境下预警探测能力有重要意义。

多雷达数据融合的目的是在一定准则下对多雷达探测数据加以分析、综合和使用,获得对探测目标的一致性解释与描述,获得比单雷达更优越的探测信息[3-4]。多雷达数据融合在融合层面可划分为信号级、检测级、点迹(跟踪级)以及航迹(情报级)四种[1]。信号级融合是直接将各雷达的探测回波进行融合处理,对时空频同步精度要求较高;检测级融合是在各雷达检测判决的基础上进行融合,对网络带宽要求较高。点迹和航迹融合是两种资源经济型融合方法,点迹融合具有信息损失少、处理精度更高、稳定性更强的优势[5],已逐渐替代航迹融合,成为现代组网雷达系统数据融合的主要手段。

多雷达点迹融合方法可分为序贯滤波方法和数据压缩方法两类[6]。序贯滤波方法[7]是将各雷达量测点迹视为平等独立的量测值,按照探测时间顺序依次代入滤波算法中,滤波过程中依据代入的点迹调整量测协方差矩阵,高低精度点迹混合滤波,提高了数据率,有利于跟踪高机动目标,但航迹精度难以保证。数据压缩方法是按照一定的权值,将某一时刻多个雷达的量测点迹综合成单个精度更高的量测值再进行滤波,航迹精度更高,但对多雷达采样周期和同步性能有一定要求。本文的研究针对多站雷达高数据率协同跟踪中近程目标的场景,采用数据压缩方法。

基于数据压缩的点迹融合常采用基于经典统计理论的融合方法,包括最小二乘、加权平均融合方法[8-9]等,主要方法是根据各雷达的精度、可靠性等性能指标为各雷达分配一个权值后进行加权融合[10-11]。贝叶斯统计理论则将每一次检验过程动态地看作是对先验知识的不断修正过程[12],文献[13]系统地论述了贝叶斯算法的基本思想,采用贝叶斯估计算法可以有效地对多源不确定性数据进行融合,并可以适应融合随时间、空间变化的数据需求,基于贝叶斯的数据融合技术在多源数据融合中得到广泛应用[14-18],但在多雷达点迹融合中缺少相关研究。

雷达点迹滤波预测的下一时刻目标位置,实际上是一种先验知识,传统基于经典统计理论的方法缺乏对先验知识的利用,不利于提高点迹融合精度。贝叶斯统计理论为基于数据压缩的点迹融合提供了新思路。本文首先基于贝叶斯理论构建一种多雷达点迹融合和滤波架构,将多雷达量测点迹视为贝叶斯理论中的观测值,将卡尔曼滤波对目标下一时刻位置的预测和预测协方差视为贝叶斯理论的先验信息;然后针对融合过程中所需的点迹标准差等信息,研究基于回波信噪比的点迹标准差在线估计方法。相对于现有的基于经典统计理论的点迹融合方法,本文建立了点迹融合与卡尔曼滤波的紧耦合框架,充分利用目标位置预测值这一先验知识,有效提高点迹融合精度和鲁棒性。本文通过仿真测试的方式对比了本文方法与单雷达滤波、航迹融合等方法的结果,验证了本文方法的有效性。

1 贝叶斯融合算法

贝叶斯统计理论相对于经典统计理论的主要区别在于是否利用先验知识,贝叶斯统计理论则是将每一次检验过程动态地看作是对先验知识的不断修正过程。假定待估计参数x的先验概率为p(x),观测值为y,贝叶斯统计理论给出了计算后验概率的方法[19-20]:

(1)

在测得一组测量数据(x1,x2,x3, …,xl)的条件下,被测参数的条件概率密度函数可表示为

(2)

(3)

其中,

(4)

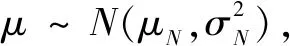
(5)

综合式(3)和式(5)可得

(6)

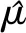
(7)

因此,式(6)可用于在已知测量数据(x1,x2,x3, …,xl)和被测量参数μ先验概率的情况下对μ进行估计。在多雷达点迹融合应用中,μ代表目标位置真值;μ0为上一时刻航迹滤波对目标距离、方位、俯仰的预测值(Rp,Ap,Ep),σ0为目标距离、方位、俯仰预测值的标准差(σR,p,σA,p,σE,p);xk为雷达k的点迹距离、方位、俯仰测量值(Rk,Ak,Ek),σk为对应的测量标准差(σR,k,σA,k,σE,k)。要求多雷达点迹与航迹预测值位于同一时空空间,且准确描述目标位置预测值和位置测量值的概率密度。

2 多雷达点迹预处理

为适应基于贝叶斯理论的数据融合对量测值的要求,对多雷达点迹进行预处理,统一时空基准,并估计量测误差。

2.1 点迹时空配准

空间配准是针对各雷达坐标原点不同,将雷达点迹转换至同一坐标系,假设雷达m点迹坐标原点在统一坐标系(大地直角坐标系)中的位置为(am,bm,cm),将雷达点迹由极坐标系转换至大地直角坐标系,并平移至统一的坐标原点得

xm=R′mcos(E′m)cos(A′m)+am
ym=R′mcos(E′m)sin(A′m)+bm
zm=sin(E′m)+cm

(8)

其中,(R′m,A′m,E′m)为雷达m空间配准前的点迹距离、方位、俯仰,(xm,ym,zm)为雷达m点迹在统一坐标系(大地直角坐标系)中的位置,再将该点迹转换回极坐标系得

(9)

式中(Rm,Am,Em)为雷达m点迹空间配准后的距离、方位、俯仰。

时间配准是针对各雷达探测时间不同,将时间相近的雷达点迹转换至同一时刻。本文采用多项式插值法进行时间配准,基本原理是利用多个时刻的点迹数据进行曲线拟合,对目标运动轨迹进行逼近,进而估计指定时刻的目标位置。假设需将雷达m点迹时间配准至tc,提取雷达m在t0、t1、t2时刻测量值x0、x1、x2,采用拉格朗日三点插值法,近似得到雷达m在tc时刻的测量值如下:

(10)

2.2 点迹误差估计

假设点迹系统差通过最小二乘等方式进行了在线校正[22],点迹误差估计则主要考虑由热噪声等引起的随机差。

距离标准差估计方法如下:

(11)

式中σTR为热噪声引起的随机误差,σXR为其他因素引起的点迹距离随机误差,包括数据量化、脉冲抖动等。σTR与信噪比SNR有直接关系。

(12)

式中τe为等效脉冲宽度,c电磁波传播速度,SNR为单次扫中信噪比。

角度标准差估计方法如下:

(13)

式中σTA为热噪声引起的随机误差,σXA为其他因素引起的点迹角度随机误差,包括扫描、闪烁等。σTA与信噪比SNR有直接关系。

(14)

式中θ0为3 dB波束宽度,Km为归一化单脉冲斜率,在1.2～2.0之间。

点迹误差估计过程中,σXR和σXA由雷达系数自身决定,不随目标改变,可由试验方法测得。σTR和σTA为噪声引起的随机误差,主要由目标回波的SNR决定。点迹误差估计方法是,利用历史的点迹SNR和误差测量数据,结合式(11)和式(13),通过最小二乘法对σXR和σXA进行估计,构建以SNR为自变量的距离、方位、仰角标准差实时估计方法。

3 多雷达点迹融合方法

贝叶斯统计理论提供了一种数据融合的方式,假设将被测量值的预测误差和测量误差均建模为高斯噪声,则可用式(6)进行点迹融合,整个点迹融合与滤波过程如图1所示。

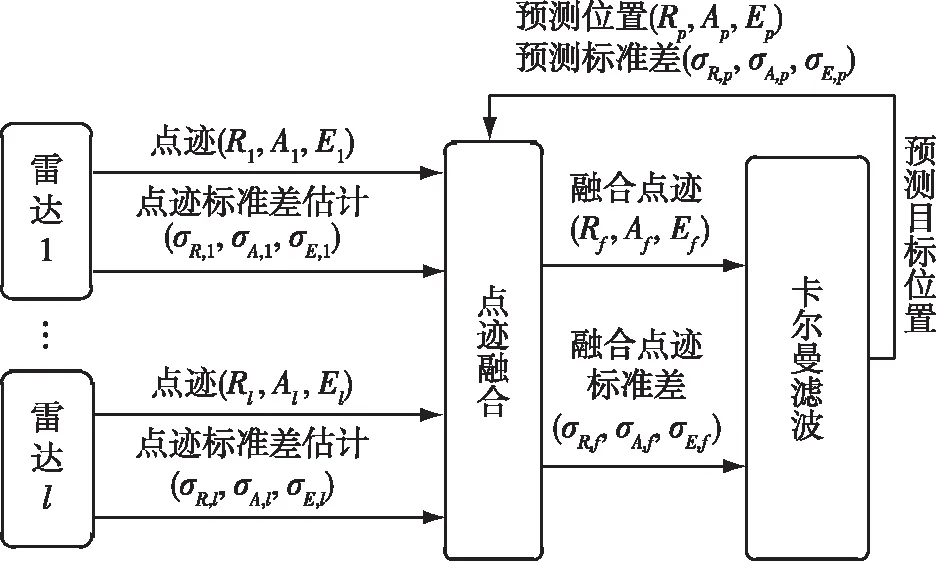
图1 点迹融合与滤波过程框图Fig.1 Block diagram of data fusion and filtering process

点迹融合前需要获知的信息包括航迹滤波对tk+1时刻的目标距离、方位、俯仰的预测值(Rp,Ap,Ep)及其预测标准差(σR,p,σA,p,σE,p),以及tk+1时刻l个雷达经时空配准后的量测值和量测标准差,雷达m的点迹距离、方位、俯仰测量值记为(Rm,Am,Em),对应的测量标准差记为(σR,m,σA,m,σE,m),对距离、方位、俯仰分别进行融合,计算方法如下:

(15)

式中(Rf,Af,Ef)为融合点迹的距离、方位、俯仰,形成量测矩阵Yk+1=[Rf,Af,Ef],标准差为(σR,f,σA,f,σE,f)。

(16)

融合点迹滤波采用卡尔曼滤波方法,并预测下一时刻目标位置。卡尔曼滤波状态转移方程如下,首先基于tk前的测量预测tk+1时刻的状态及其协方差

(17)

P(k+1|k)=φ(tk)P(k|k)φ(tk)T+Q(tk)

(18)

(19)

然后利用融合点迹形成的量测矩阵Yk+1更新目标状态及其协方差

(20)

P(k+1|k+1)=[I-Kk+1H(tk+1)]P(k+1|k)

(21)

其中,卡尔曼增益为

Kk+1=P(k+1|k)HT(tk+1)×
[H(tk+1)P(k+1|k)HT(tk+1)+Rk]-1

(22)

进而利用式(17)预测t+2时刻目标位置,利用式(18)得到预测方差,等待t+2时刻各雷达点迹时空配置结果,继续进行下一次点迹融合。

4 仿真分析

为验证本文所提点迹融合方法对提高目标位置估计精度的作用,作者设计了仿真试验,产生两种雷达的探测点迹,分别称为高波段雷达和低波段雷达。作者采用4种处理方法产生航迹,方法1是单独对高波段雷达点迹进行卡尔曼滤波处理,产生航迹;方法2是单独对低波段雷达点迹进行卡尔曼滤波处理,产生航迹;方法3是对高低波段雷达的航迹进行融合处理,按照航迹估计协方差进行加权融合;方法4是采样本文提出的点迹融合与滤波方法进行处理。

研究人员在仿真试验中模拟高低波段雷达测量点迹选取的目标理论轨迹如图2所示,包含平飞、爬升、转向等典型的运动形态。根据典型的高低波段雷达搭配使用方式,高波段雷达作为近程精确跟踪,探测精度高但作用距离近,低波段雷达作为远程预警,探测精度稍差但探测距离远。根据雷达方程,在目标RCS恒定的情况下,回波信噪比主要受目标距离影响。仿真中根据目标距离,结合高波段、低波段雷达的辐射功率、收发增益等参数设定,计算目标回波信噪比和点迹标准差,通过在理论轨迹上叠加高斯噪声的方式获取仿真点迹。

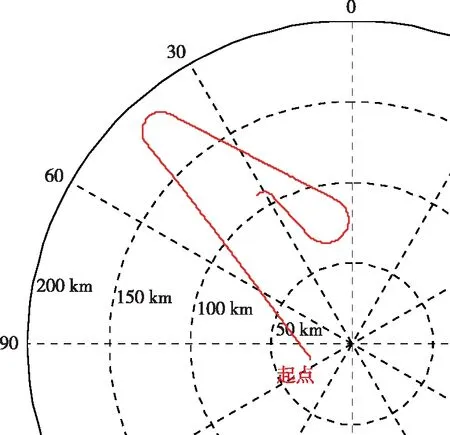
图2 仿真目标理论轨迹Fig.2 Theoretical trajectory of the simulation target

目标距离随时间的变化如图3所示,图4为高波段雷达模拟点迹的俯仰值,在目标距离较近时维持较高的探测精度,随着目标远离、信噪比迅速下降,探测精度显著恶化。图5为低波段雷达模拟点迹的俯仰值,保精度探测距离大于目标最远距离,对目标探测精度基本保持恒定。对比图4和图5,高波段雷达在目标距离近时探测精度优于低波段雷达,在目标距离远时劣于低波段雷达。点迹仿真创造了两雷达探测精度随时间变化且在不同时期互有优劣的情形。

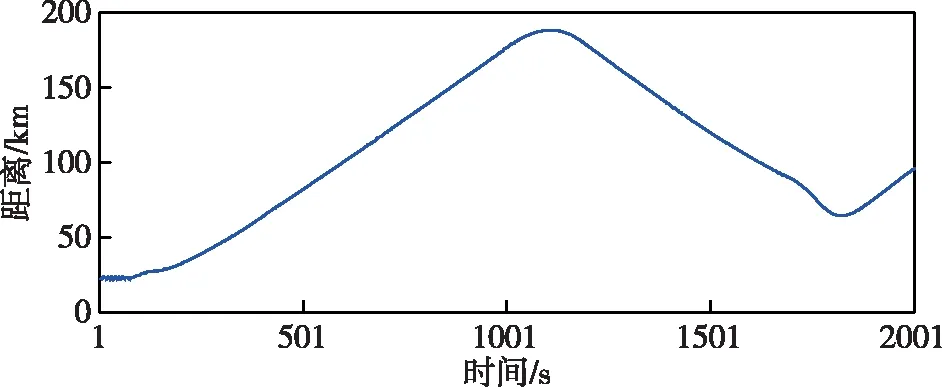
图3 目标距离Fig.3 The range of the simulation target

图4 高波段雷达点迹俯仰值Fig.4 The elevation of the high wavelength radar point

图5 低波段雷达点迹俯仰值Fig.5 The elevation of the low wavelength radarpoint

仿真试验中使用4种方法处理高波段雷达和低波段雷达的仿真点迹,获得4种航迹数据,分别计算一次差,图6和图7分别给出了方法1和方法2处理所得航迹的俯仰一次差结果。方法1仅使用高波段雷达点迹进行滤波,受点迹精度影响明显,在目标距离远点迹精度差时,俯仰误差较大。方法2仅使用低波段雷达点迹进行滤波,点迹误差基本恒定,航迹误差也维持较为恒定的结果,在目标近时劣于方法1结果,在目标远时优于方法1结果,与高低波段雷达点迹精度差别一致。

图6 方法1高波段雷达点迹滤波结果一次差Fig.6 The error of high wavelength radar track

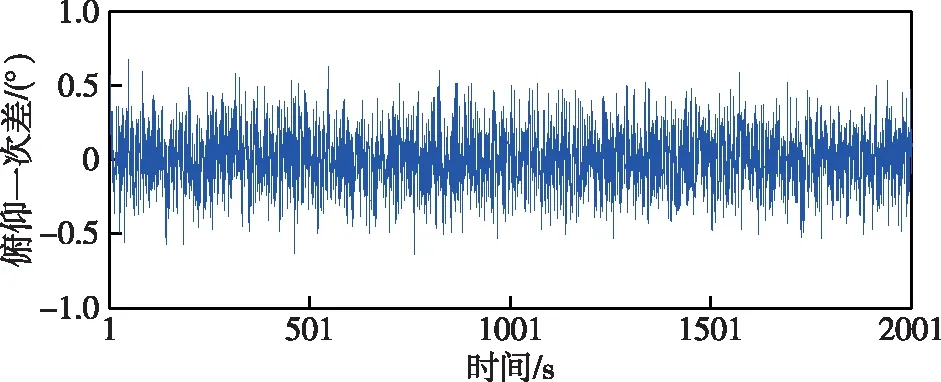
图7 方法2低波段雷达点迹滤波结果一次差Fig.7 The error of low wavelength radar track

图8和图9分别是方法3和方法4处理所得航迹的俯仰一次差结果,方法3是高低波段雷达航迹融合处理结果,方法4是利用本文提出的方法进行高低波段雷达点迹融合处理结果。由于在目标距离远时高波段雷达点迹误差大,单独滤波所得航迹误差大,影响航迹融合结果。本文提出的点迹融合方法,全程俯仰误差无明显起伏,一次差优于航迹融合结果。

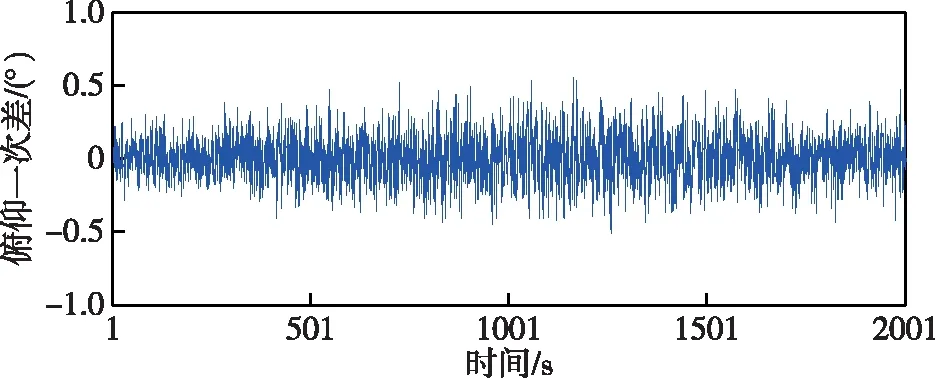
图8 方法3高低波段雷达航迹融合一次差Fig.8 The error of radar track fusion

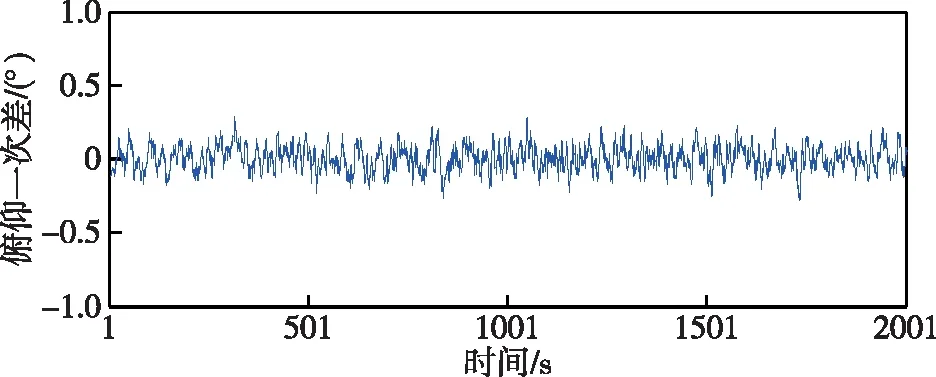
图9 方法4高低波段雷达点迹融合一次差Fig.9 The error of point fusion

为综合比较4种方法的滤波精度,作者进行500次蒙特卡洛仿真,统计距离、方位、俯仰最大误差,结果如表1所示。航迹融合的距离最大误差介于高低波段雷达单独滤波结果之间,方位、俯仰最大误差略优于高低波段雷达单独滤波结果,本文提出的点迹融合结果优于航迹融合结果和高低波段雷达单独滤波结果。结果表明,本文方法有效提高了对目标位置的估计精度。

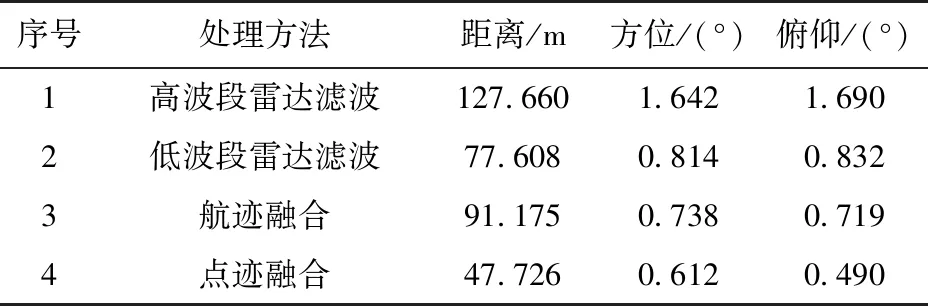
表1 目标航迹最大误差比较

5 结束语

本文基于贝叶斯理论提出了一种多雷达点迹自适应融合方法,将贝叶斯融合算法与卡尔曼滤波结合,以卡尔曼滤波量测预测作为贝叶斯理论的先验知识,并利用目标回波信噪比实时估计点迹标准差,构建权重自适应调整的多雷达数据压缩架构。仿真结果表明,本文提出的基于贝叶斯理论构建的点迹融合滤波架构,能够有效提高对目标航迹的估计精度,且能够适应点迹精度随信噪比、干扰变化的场景,具有较强的鲁棒性。