含修正Yukawa-Kratzar势场的Schr?dinger方程束缚态解析解
2023-06-11陈文利史艳维冯晶晶樊亚云
陈文利 史艳维 冯晶晶 樊亚云

摘 要:采用Greene-Aldrich指數型近似方法近似表达径向方程非线性离心项,利用P-NU方法研究了含修正Yukawa-Kratzar势场的Schr?dinger方程束缚态解析解问题,得到了归一化的束缚态波函数和相应能量本征值方程,数值求解能量本征值方程并和真实值数据进行了对比。
关键词:修正Yukawa-Kratzar势场;束缚态;薛定谔方程;近似解析解
中图分类号:O365文献标志码:A文章编号:1001-2443(2023)01-0041-06
引 言
在量子力学体系中,薛定谔方程的束缚态解析解是寻求理解物理系统量子信息的有效手段,其主要研究系统的离散能量本征值和本证态。诸多解析求解办法被提出来解决不同势场的薛定谔方程的束缚态解析解问题,例如,超对称方法(SUSYQM)[1], NU (Nikiforov–Uvarov) 方法[2], P-NU(Parametric Nikiforov–Uvarov)方法[3-4] , AIM 方法[5]等。其中,P-NU方法是将带离心项的薛定谔方程转为多参数的非线性微分方程进行求解,能够快速有效的获得系统的解析解。
标准的Kratzar势场[Vr=-De2re/r-re2/r2],其在[r=re]取到最小值[-De],修正的Kratzar势场是在标准的Kratzar势场添加一个[De]项,表达式中[1r]项归因于特定离子分子中的库仑势能,带有[1r2]项是和电子动能相关。C. Berkdemir利用NU方法解析求解该势场的能量本征值和相应波函数,并计算了[N2,][CO,NO]和[CH]分子能量本征值[6-7], 修正的Yukawa模型在研究双原子[Cl2]和[N2]等的热力学性质的问题上已经被证实为有效的研究分子热力学性质的模型[8]。由于组合势场能提供更为广泛的应用,在基于修正的Kratzar势场和修正的Yukawa势场的基础上构造出了更为复杂的修正的Yukawa-Kratzar组合势场,其表达式为[9]
其中,[V0]是势场强度,[α]为是势屏参数,[De]为离解能,[re]为平衡键长,当[V0=0]时势场可退化为修正的Kratzar势,当[De=0]时势场可退化为修正的Yukawa势场。首先,势函数展开后势函数中主要含有指数形式结构,此结构对于含离心项的薛定方程解析解求解将带来较大挑战。另一方面,在文献[9]中,R.H.Parmar等利用P-NU方法和超对称方法求解该势场的Klein–Gordon方程的解析解,在文献[8]中,U. S. Okorie利用超几何函数法求解了修正的Yukawa势场薛定方程解析解,获得了系统的能量方程, 但修正的Yukawa-Kratzar组合势场的薛定谔方程束缚态解析解问题尚未见报道。本文拟采用Greene-Aldrich近似方法近似表达系统的非线性离心项[10],分别用了P-NU方法和超几何函数法求解修正的Yukawa-Kratzar组合势场的薛定谔方程任意[l]态束缚态解析解,并推导出系统的能量本征值方程和波函数方程。同时,数值求解了能量本征值数据并和程序包所得真实数据进行比较,验证了本文推导的正确性。
不难发现,经过简单的推导,超几何函数法所获得的能量本征值方程(23)和参数P-NU方法所得的本征值方程(10)本质是一致的,也进一步验证了本文推导的准确性。
3 数值结果与讨论
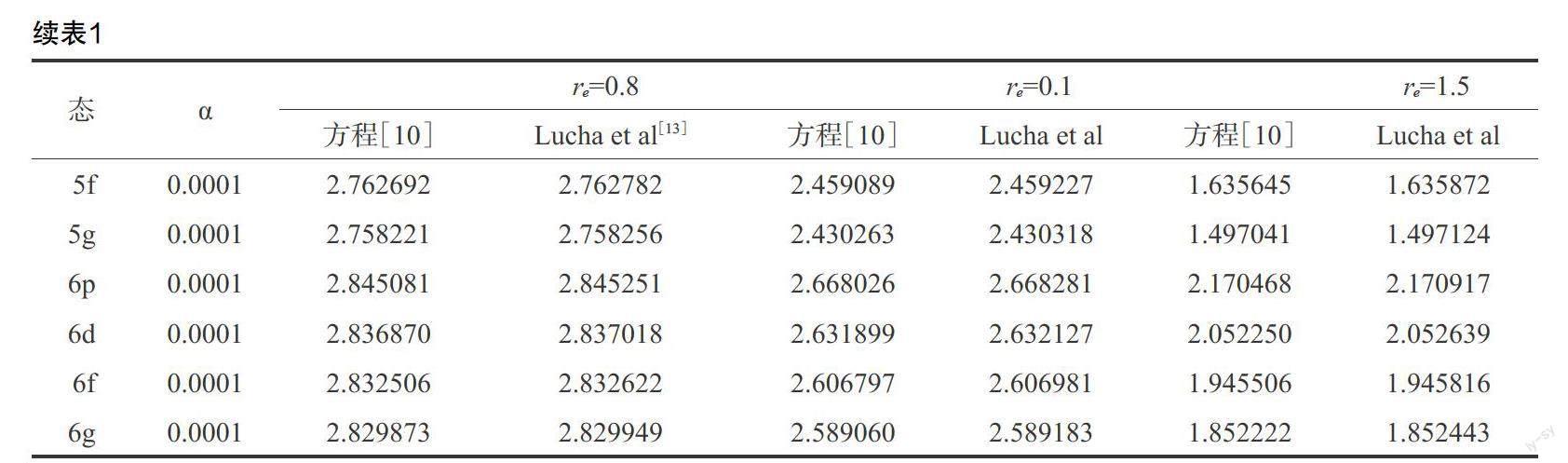
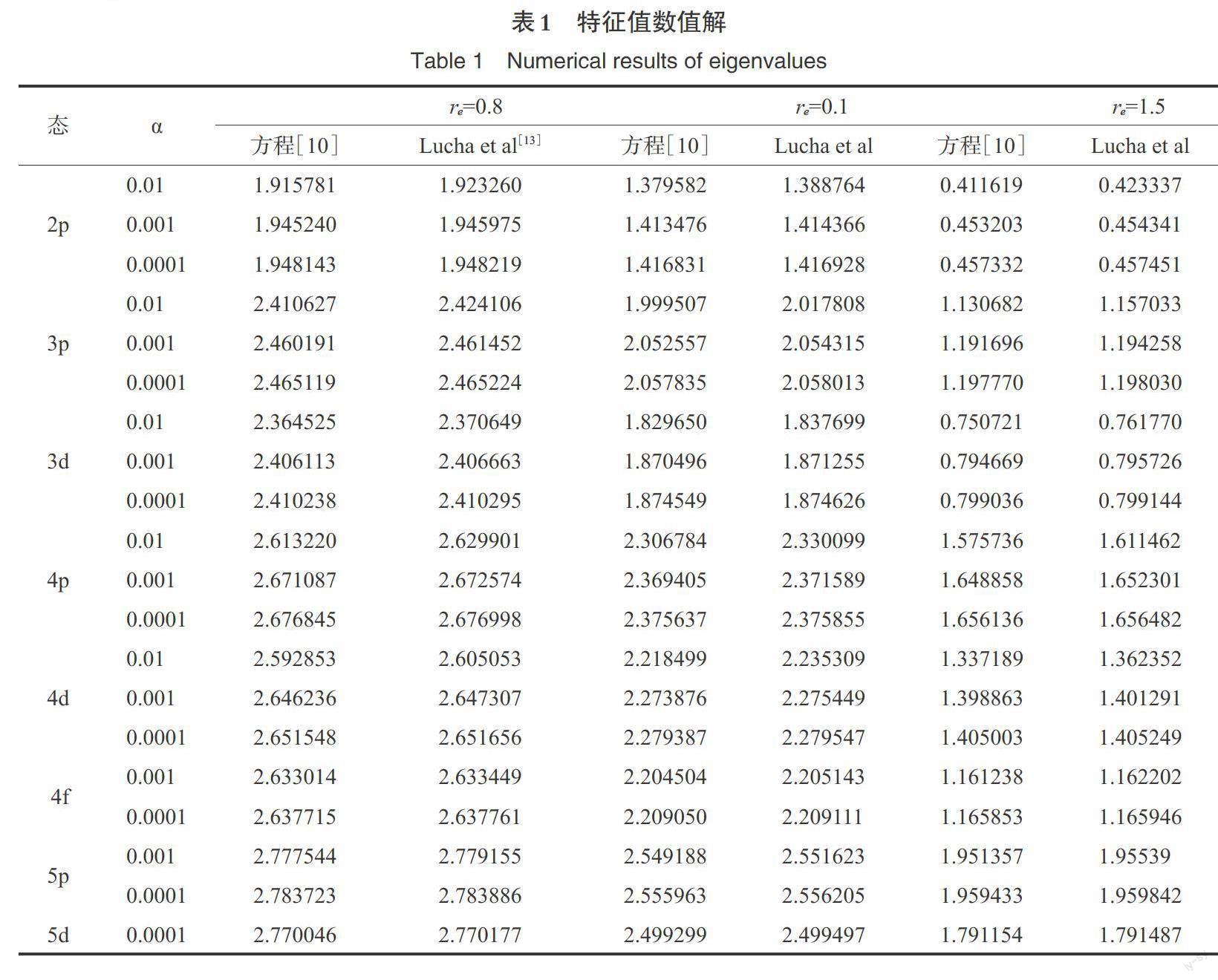
首先,取势参数[De=6,V0=3,] 数值求解能级方程(10)在[2p,3p,3d,4p,4d,4f,5p,5d,5f,5g,][6p,6d,6f,6g]态[re=0.8,1.0,1.5]的能量本征值数据,并将获得的能级数据与MATHEMATICA程序包[14]所获得数据进行比较,详见表1。本文所推导出的能级数据较好的逼近了真实值,同时,当α越逼近零时,能量数据逼近于真实值精度越高,这一点和近似公式的近似精度要求是一致。
别数值求解两种退化后势场对应系统的本征值数据,并和程序包和先前文献中已获得数据进行比较,详见表2。从对比数据不难看出,本文获得了修正的Yukawa势场和修正的Kratzar势场都较好的逼近了真实值.
4 结 论
P-NU方法是求解量子系统的有效代数方法,本文采用该方法研究了修正的Yukawa-Kratzar势场的Schr?dinger方程束缚态解析解问题,采用Greene-Aldrich指数型近似方法近似表达径向方程非线性离心项,将径向方程转化为适合应用P-NU方法求解的非线性微分方程,获得了系统的任意[l]态能量本征值和含有雅克毕函数表示的复杂波函数,并借助归一化条件,计算出归一化常数. 最后从两个层面验证本文推导的正确性,首先,利用传统的超几何函数法重新进行了能量本征值的推导,获得了和P-NU方法所得一致的能量方程,自洽的验证了推导的正确性;其次,从数值解方面进行了验证,我们将所计算出的能量本征值数据与MATHEMATICA程序包所计算的数据进行了比较,同时,取定不同参数将修正Yukawa-Kratzar势场退化为修订的Yukawa势场和修订的Kratzar势场,并与退化后的两种势场能量本征值数据与先前文献已知数据和程序包计算所得数据进行了比较,当屏参数[α]趋向于零时,能量本征值越逼近于真实值,这个结论与Greene-Aldrich指数型近似性质是一致。
参考文献:
[1] COOPER F, KHARE A, SUKHATME U, Supersymmetry and quantum mechanics[J]. Phys Rep, 1995,251: 267–365.
[2] PARMAR R.H. Generalized improved non-central potential and solution of Schr?dinger equation with extended ring-shaped potential via Nikiforov-Uvarov method[J].Eur Phys J Plus, 2019,134(86): 12513-6.
[3] IKOT A N, OKORIE U S, AMADI P O,et al.The Nikiforov–Uvarov-Functional analysis (NUFA) method: a new approach for solving exponential-type potentials[J].Few-Body Syst,2021,62(1):9.
[4] TEZCAN C, SEVER R, A general approach for the exact solution of the schr?dinger equation[J]. Int J Theor Phys, 2009,48:337–350.
[5] BAYRAK O, BOZTOSUN I, CIFTCI H. Exact analytical solutions to the Kratzer potential by the asymptotic iteration method[J]. Int J Quantum Chem, 2007, 107:540-544.
[6] BERKDEMIR C, BERKDEMIR A, HAN J G.Bound state solutions of the Schr?dinger equation for modified Kratzers molecular potential[J]. Chem Phys Lett,2006,417:326-329.
[7] ONYENEGECHA C P, NJOKU I J, OMAME A, et al. Dirac equation and thermodynamic properties with the modified Kratzer potential[J].Heliyon,2021,7:e08023.
[8] OKORIE U S, IBEKWE E E. Thermodynamic properties of the modified Yukawa potential[J]. J Korean Phys Soc,2018,73(9):1211-1218.
[9] PARMAR R H, VINODKUMAR P C .Eigensolution of the Klein–Gordon equation for modified Yukawa–Kratzer potential and its applications using Parametric Nikiforov–Uvarov and SUSYQM method[J]. J Math Chem,2021,59:1638–1703.
[10] GREEN R L, ALDRICH C. Variational wave functions for a screened Coulomb potential[J].Phys Rev A, 1976,14(6):2363-2366.
[11] CHEN W L,OKON I B. Pseudospin symmetric solutions of the Dirac equation with the modified Rosen–Morse potential using Nikiforov–Uvarov method and supersymmetric quantum mechanics approach[J].Chin Phys B,2022,31(5):134-139.
[12] ANTIA A D, OKON I B, ISONGUYO C N, et al. Bound state solutions and thermodynamic properties of modified exponential screened plus Yukawa potential[J].J Egypt Math Soc,2022,30:11.
[13] GRADSHTEYN S, RYZHIK I M, Tables of integrals, series, and products, fifthed[M]. New York: Academic Press,1994:1-50.
[14] LUCHA W, SCH?BERL F F. Solving the schr?dinger equation for bound states with MATHEMAICA 3.0[J].Int J Mod Phys C,1999,10(4):607-619.
The Bound State Analytical Solutions of Schr?dinger Equation with the Modified Yukawa-Kratzer Potential Model
CHEN Wen-li, SHI Yan-wei, FENG Jing-jing, FAN Ya-yun
(School of Intelligent Science and Information Engineering, Xi'an Peihua University, Xi'an 710125, China)
Abstract: The nonlinear centrifugal terms of the radial equation are approximated by the Greene-Aldrich exponential form approximation method. The bound state analytical solution of the Schrodinger equation with improved Yukwa-Kratzar potential is studied by P-NU method. The normalized bound state wave function and corresponding energy eigenvalues are obtained. The energy eigenvalue equation is solved numerically and compared with the real value data.
Key words: the modified Yukawa-Kratzer potential; bound states; Schr?dinger equation; approximately analytical solutions
(責任编辑:马乃玉)
