一类具有时滞和修正Leslie-Gower项捕食模型的Hopf分支

王雅迪 袁海龙

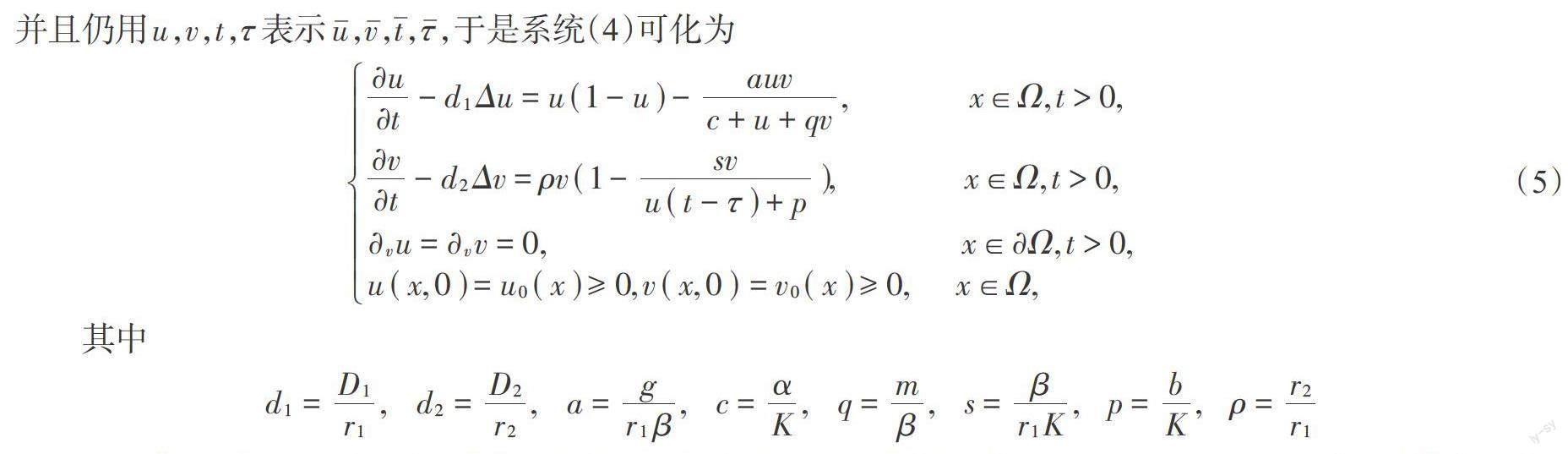
摘 要：主要研究在齐次Neumann边界条件下的一类带有修正Leslie-Gower项和Beddington-DeAngelis功能反应的时滞扩散捕食模型。首先，以时滞参数作为分支参数，研究了时滞效应对该捕食模型正常数平衡点稳定性的影响，并得到了产生Hopf分支的条件；其次，利用偏泛函微分方程的规范型理论和中心流形定理，给出了Hopf分支方向和分支周期解的稳定性；最后，借助MATLAB软件进行数值模拟，验证结论。

关键词：Hopf分支； 时滞；捕食-食饵模型； 修正Leslie-Gower；稳定性

中图分类号：O175.12文献标志码：A文章编号：1001-2443（2023）01-0022-13

引 言

捕食关系作为自然界中最重要和最广泛的种间关系之一，在生物种群现象的研究中起到至关重要的作用。近年来，众多学者通过对捕食-食饵模型的探讨，取得了非常丰富的研究成果［1-4］。2011年，Melese和Gakkhar［5］研究了如下带有修正Leslie-Gower项和Beddington-DeAngelis功能反应函数的捕食-食饵模型

其中[u]和[v]分别表示食饵和捕食者的种群数量；[r1]和[r2]分别表示食饵和捕食者的内禀增长率；[K]表示食饵的最大环境容纳量；[g]表示最大消耗速率；[α]表示饱和常数；[m]代表捕食者干扰；模型中所有参数均为正数。其中[gu/α+u+mv]是Beddington-DeAngelis功能反应函数，反映了捕食者的捕食能力对食饵数量规模的饱和反应；修正Leslie-Gower项[βv/u+b]的建立是基于当捕食者在所偏爱的食饵匮乏情况下，转向去获取其它食物来源的假设。

考虑（1）在齐次Neumann边界条件下的扩散系统

其中[Ω?RN（N≥1）]为具有光滑边界[?Ω]的有界开集；[ν]是[?Ω]上的单位外法向量；[Δ]是拉普拉斯算子；[D1]和[D2]分别表示食饵和捕食者的扩散系数，均为正常数。

对于系统（2），Melese和Gakkhar［5］讨论了唯一正平衡点的局部渐近稳定性，并指出在某些条件下Turing不稳定将不会在该平衡点处产生；Yang［6］利用比较原理方法研究了唯一正平衡点的全局渐近稳定性；陈平和胡广平［7］则研究了Turing不稳定出现的条件及时空模式的存在性，并对无扩散影响的空间齐次系统，分析了正平衡点的稳定性以及Hopf分支的存在性；此外，Li［8］等人研究了一类脉冲扩散捕食系统，利用比较原理和Lyapunov函数得到了系统存在唯一全局稳定周期解的条件。

在现实自然界中，时间滞后现象普遍存在，因此将时滞效应引入到生物模型中，有利于对系统动力学行为做更深入、全面的研究。Yang和Wei［9］在系统（2）的基础上，考虑了如下时滞反应扩散模型

其中[τ]代表时滞参数，对于此系统，他们研究了时滞对非负平衡点稳定性的影响以及Hopf分支.Yang和Zhang［10］则考虑在时滞模型（3）基础上加入食饵避难常数后系统的动力学行为。此外，Liu［11］考虑给系统（1）引入反馈时滞，则有

并研究了其系统的局部稳定性和Hopf分支。

基于以上分析，本文在系统（2）的基础上考虑如下模型

其中，时滞[τ]代表捕食者的成熟期。为了书写方便，作无量纲变换，令

受生物种群在繁衍过程中成熟期的影响，当前时态的种群增长率总是与之前某一时态的种群数量有关。在此生物学背景下，考虑给系统（2）中捕食者种群引入时滞后，本文分别对常微和偏微系统研究了时滞效应对正常数平衡点稳定性的影响，以及在正常数平衡点处Hopf分支产生的条件，并计算了分支周期解的稳定性和分支方向.结果表明，当时滞参数[τ]在经过某一临界值时，系统会由稳定状态变为不稳定状态，并产生Hopf分支。文中分别用[?0]和[?+]表示非负整数集和正实数集。

1 正常数平衡点的稳定性和Hopf分支的存在性

1.1 带时滞的常微分系统

本节考虑如下带有时滞参数的常微分系统

取[τ=3.46>τ0]和初值[u（x，t）=u*+0.05tsin（0.54x）]，[v（x，t）=v*+0.05tsin（0.54x）]，因此由定理1.4和定理2.1可知系统（14）在正常数平衡点[（u*，v*）]处产生Hopf分支，如图4。

4 结 论

本文提出了一个带有修正Leslie-Gower项和Beddington-DeAngelis功能反应的时滞扩散捕食模型，研究时滞对该模型动力学行为的影响。利用稳定性理论讨论了该系统平衡点处局部稳定性和Hopf分支发生的条件，并通过中心流形定理和规范型理论分析了Hopf分支的方向和周期解的穩定性。数值模拟出该系统在不同时滞作用下的时间序列图。从数值模拟结果中可以看出，系统（6）和（14）中时滞参数发生变化时其生态意义有如下变化：当时滞参数小于某个临界值时，捕食者和食饵的种群密度会在特定区域内趋于一个正平衡态，保持稳定；而当时滞参数超过该临界值时，两种群的密度变化会呈现周期振荡模式。因此时滞效应是影响捕食系统种群密度变化的一个重要因素。

参考文献：

［1］ CHEN S S， SHI J P， WEI J J. The effect of delay on a diffusive predator-prey system with Holling type-Ⅱ predator functional response［J］. Communications on Pure & Applied Analysis， 2013， 12： 481-501.

［2］ LI L Y， MEI Y Y， CAO J Z. Hopf bifurcation analysis and stability for a ratio-dependent predator-prey system with time delay［J］. International Journal of Bifurcation and Chaos， 2020， 30（3）： 2050037.

［3］ 赵童， 袁海龙. 一类具有时滞的捕食—食饵模型的Hopf分支［J］. 安徽师范大学学报（自然科学版）， 2022， 45（2）： 121-130.

［4］ ZHU Y， WANG K. Existence and global attractivity of positive periodic solutions for a predator-prey model with modified Leslie-Gower holling type II schemes［J］. Journal of Mathematical Analysis and Applications， 2011， 384： 400-408.

［5］ MELESE D， GAKKHAR S. Stability analysis of a predator-prey model with Beddington-DeAngelis functional response ［J］. Plant， Soil and Environment-UZPI（Czech Republic）， 2011， 15（2）： 65-71.

［6］ YANG W S. Global asymptotical stability and persistent property for a diffusive prey-predator system with modified Leslie-Gower functional response［J］. Nonlinear Analysis： Real World Applications， 2013， 14（3）： 1323-1330.

［7］ 陳平， 胡广平. 一类具有B-D反应项的扩散捕食系统的稳定性和Turing模式［J］. 西北师范大学学报（自然科学版）， 2020， 56（2）： 15-20.

［8］ LI X Y， WANG Q， HAN R J. An impulsive predator-prey system with modified Leslie-Gower funtional response and diffusion［J］. Qualitative Theory of Dynamical Systems， 2021， 20（3）： 1-20.

［9］ YANG R Z， WEI J J. The effect of delay on a diffusive predator-prey system with modified Leslie-Gower functional response［J］. Bulletin of the Malaysian Mathematical Sciences Society， 2017， 40（1）： 51-73.

［10］ YANG R Z， ZHANG C R. Dynamics in a diffusive predator-prey system with a constant prey refuge and delay［J］. Nonlinear Analysis： Real World Applications， 2016， 31： 1-22.

［11］ LIU J. Dynamical analysis of a delayed predator-prey system with modified Leslie-Gower and Beddington-DeAngelis functional response［J］. Advances in Difference Equations， 2014， 2014（1）： 1-19.

［12］ WU J H. Theory and Applications of Partial Functional Differential Equations［M］. New York： Springer， 1996：1-448.

［13］ LIN X D， SO W H， WU J H. Center manifolds for partial differential equations with delays［J］. Proceedings of the Royal Society of Edinburgh， 1992， 122（3-4）： 237-254.

［14］ HASSARD B D， KAZARINOFF N D， WAN Y H. Theory and Applications of Hopf Bifurcation［M］. Cambridge： Cambridge University Press， 1981：1-499.

Hopf Bifurcation Analysis of a Predator-Prey Model with Modified Leslie-Gower Functional Response and Time Delay

WANG Ya-di， YUAN Hai-long

（School of Mathematics and Data Science， Shaanxi University of Science and Technology， Xi'an 710021， China）

Abstract： In this paper， a diffusive modified Leslie-Gower-type predator-prey model with time delay and Beddington-DeAngelis functional response subject to Neumann boundary condition is considered. By choosing the time delay as the bifurcation parameter， the stability/instability of the unique positive constant equilibrium and the existence of Hopf bifurcation are investigated. In addition， the formulae to determine the direction of the Hopf bifurcations and the stability of the bifurcating periodic solutions by applying the theory of normal form and center manifold for partial differential equation are derived. Finally， some numerical simulations are carried out to support the analytical results.

Key words： Hopf bifurcation； time delay； predator-prey model； modified Leslie-Gower； stability

（责任编辑：马乃玉）