EVO公式对高度近视白内障患者术后屈光力的预测性分析

李典蓉 段丽 张明媚 李瑶 熊亚楠 朱涛 张宏*

高度近视（high myopia，HM）是指眼轴长度（AL）≥26 mm 或屈光度≤-6.0D 的近视性疾病，由于AL 延长及氧化应激反应等，可导致患者出现一系列影响视力的并发症，如白内障、黄斑病变和视网膜病变等［1］。手术是治疗高度近视并发白内障的主要方式，但有良好的术后视觉效果仍存在一定难度。为了提高患者术后视觉质量，减少屈光误差的产生，IOL 计算公式不断更新。研究认为新型公式中的EVO 公式在高度近视患者IOL 预测中表现良好［2］，本研究旨在比较高度近视患者IOL 度数计算中EVO 公式、Holladay 公式、Haigis 公式及Barrett Universal Ⅱ公式平均绝对屈光误差（mean absolute error，MAE），进一步评估EVO 公式的预测准确性和稳定性，这对高度近视白内障患者术后获得理想屈光状态、提高生活质量具有重要意义。

1 资料与方法

1.1 临床资料 选择2019 年7 月至2022 年1 月本院眼科确诊为高度近视合并白内障，且行Phaco+IOL 植入术患者95 例（135 眼）。纳入标准：①经IOL Master 500 测量眼轴≥26 mm；②无其他高度近视并发症；③术前术后检查资料完整，按时随访。排除标准：①视力、屈光度、眼轴长度、角膜曲率等无法配合测量；②既往有其他眼部疾病或眼部手术史；③术中、术后出现手术并发症者。依据AL 分为3 组，A 组（26 mm ≤AL＜28 mm）39 例53 眼，B 组（28 mm ≤AL＜30 mm）41例53 眼，C 组（AL ≥30 mm）21 例29 眼。本研究经本院伦理审查委员会批准，患者均签署知情同意书。

1.2 方法 （1）术前检查：所有患者术前常规进行全面眼科检查，如视力、眼压、裂隙灯检查、眼部超声、角膜内皮计数（EM-3000）、UBM（SW-3200L）、IOL Master 500（德国 蔡司）等，采用IOL Master 进行眼球生物学参数测量。（2）手术及随访：按照每个入组对象的不同情况，选择适宜型号及度数的IOL，并分别使用Holladay 公式、Haigis 公式、Barrett Universal Ⅱ公式及EVO 公式，计算得出每个公式的术后理论屈光度。对所有患者均于表面麻醉下行Phaco+IOL，术中植入预先选择好的IOL。术后进行随访，在术后1 个月屈光状态稳定时由验光师以验光仪所测数值为基础，进行插片验光检查，并记录术后实际屈光度。计算ME 及MAE。

1.3 统计学方法 采用SPSS 25.0 统计软件。符合正态分布的计量资料以（±s）表示，多组间比较采用单因素方差分析，两两比较时采用LSD 检验。偏态分布计量资料以M（Q1，Q3）表示，采用Kruskal-Wallis 秩和检验。计数资料组间比较采用卡方检验。采用Spearman秩相关分析AL 与MAE 的相关性。P＜0.05 为差异有统计学意义。

2 结果

2.1 基线资料 三组患者年龄、性别构成比、手术眼、角膜最平坦曲率（K1）及角膜最陡峭曲率（K2），差异无统计学意义（P＞0.05），见表1。

表1 三组患者基线资料比较

2.2 3 组中不同IOL 公式间ME 比较 Holladay 公式、Haigis 公式、Barrett Universal Ⅱ公式及EVO 公式大部分ME 为正值，表明使用这四种公式对高度近视白内障患者术后屈光度进行预测时，普遍存在远视漂移的情况，见图1。

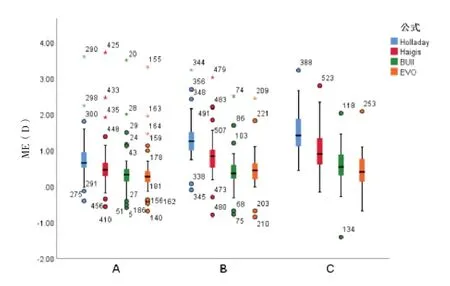
图1 3组四种公式的ME

2.3 同组中四种公式MAE 比较 3 组中，Holladay 公式、Haigis 公式、Barrett Universal Ⅱ公式及EVO 公式间MAE 差异有统计学意义（P＜0.001），A 组MAEHolladay高于MAEEVO、MAEBUII和MAEHaigis（P＜0.001、P＜0.001、P=0.02），表 明26 mm ≤AL＜28 mm 时，EVO 公 式、Barrett Universal Ⅱ公式及Haigis 公式的预测准确性相当且优于Holladay 公式。B 组MAEEVO与MAEBUII间差异无统计学意义（P=1.00），其余公式间MAE 差异有统计学意义（P＜0.05）。表明28 mm ≤AL＜30 mm 时，EVO公式与Barrett Universal Ⅱ公式预测准确性相当且优于Haigis 公式和Holladay 公式。C 组MAEEVO与MAEBUII间差异无统计学意义（P=0.99），MAEBUII与MAEHaigis间差异无统计学意义（P=1.00），其余公式的MAE 差异有统计学意义（P＜0.05）。表明当AL ≥30 mm 时，EVO 公式与Barrett Universal Ⅱ公式的预测准确性相当，Barrett Universal Ⅱ公式与Haigis 公式的预测准确性相当，但EVO 公式预测准确性优于Haigis 公式，而Holladay 公式预测准确性低于其他三种公式。见表2 及图2。

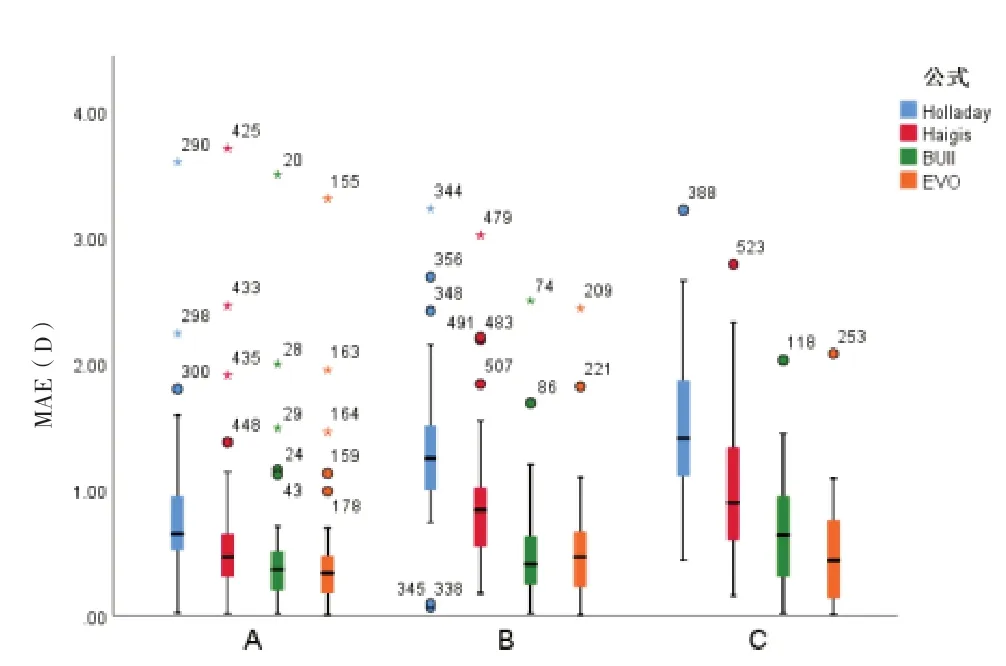
图2 同组中四种公式的MAE分布

表2 同组中四种公式的MAE比较［M（Q1，Q3）］

2.4 同一公式在三组中的MAE 比较 Holladay 公式、Haigis 公式及Barrett Universal Ⅱ公式在A、B、C 组中MAE 差异有统计学意义（P＜0.05），即Holladay 公式、Haigis 公式和Barrett Universal Ⅱ公式的MAE 受AL 影响大。EVO 公式在A、B、C 组中的MAE 差异无统计学意义（P＞0.05），即EVO 公式的MAE 受AL 影响较小，其预测稳定性优于Holladay 公式、Haigis 公式、Barrett Universal Ⅱ公式。三个AL 亚组进行两两比较，MAEHolladay与MAEHaigis在B组及C组间差异无统计学意义（P＞0.05），但在A 组与B 组及A 组与C 组间差异有统计学意义（P＜0.05），表明在26.0 mm ≤AL＜28.0 mm 与AL ≥30.0 mm 时Holladay 公式与Haigis 公式的预测准确性有明显差异。而Barrett Universal Ⅱ公式在A 组与C 组间MAE 差异有统计学意义（P=0.02），表明Barrett Universal Ⅱ公式预测准确性在26.0 mm ≤AL＜28.0 mm与AL ≥30.0 mm 时有明显差异。见表3 及图3。

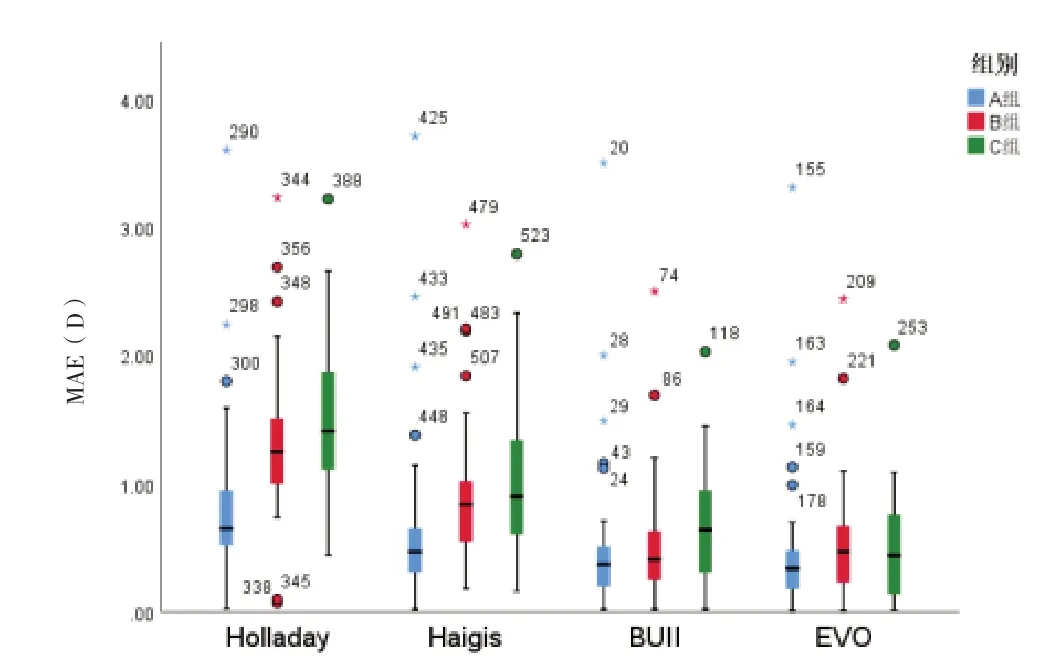
图3 同一公式在三组中的MAE分布

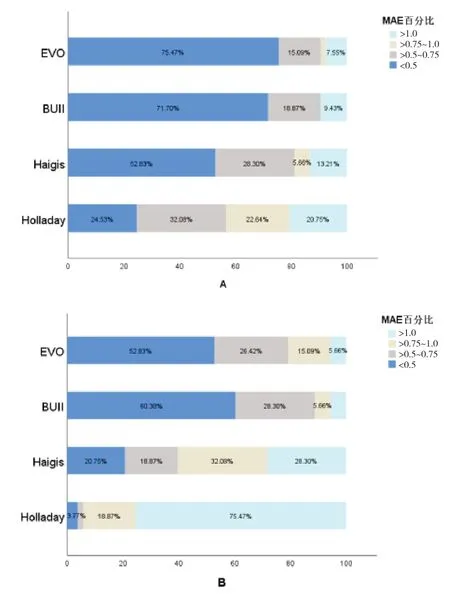
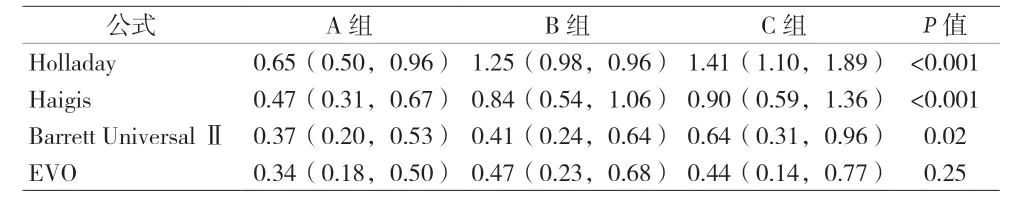
表3 同一公式在三组中MAE比较［M（Q1，Q3）］

2.5 四种公式MAE 分别在不同屈光阈值范围内的百分比 B 组及C 组中，低于0.5D 屈光阈值范围内MAEHolladay和MAEHaigis的百分比低于Barrett UniversalⅡ公式及EVO 公式，表明当AL ≥28 mm 时使用Holladay 公式和Haigis 公式进行术后屈光度预测时产生的屈光误差大于Barrett Universal Ⅱ公式及EVO 公式。MAEHolladay和MAEHaigis在A 组中低于0.5D 屈光阈值百分比高于B 组及C 组，表明这两种公式的预测准确性受AL 影响明显。使用Barrett Universal Ⅱ公式及EVO 公式进行IOL计算时产生的屈光误差相似且低于Holladay公式和Haigis 公式，另外Barrett Universal Ⅱ公式及EVO公式有89.63%及93.33%的屈光误差在1.0D 以内。见图4。

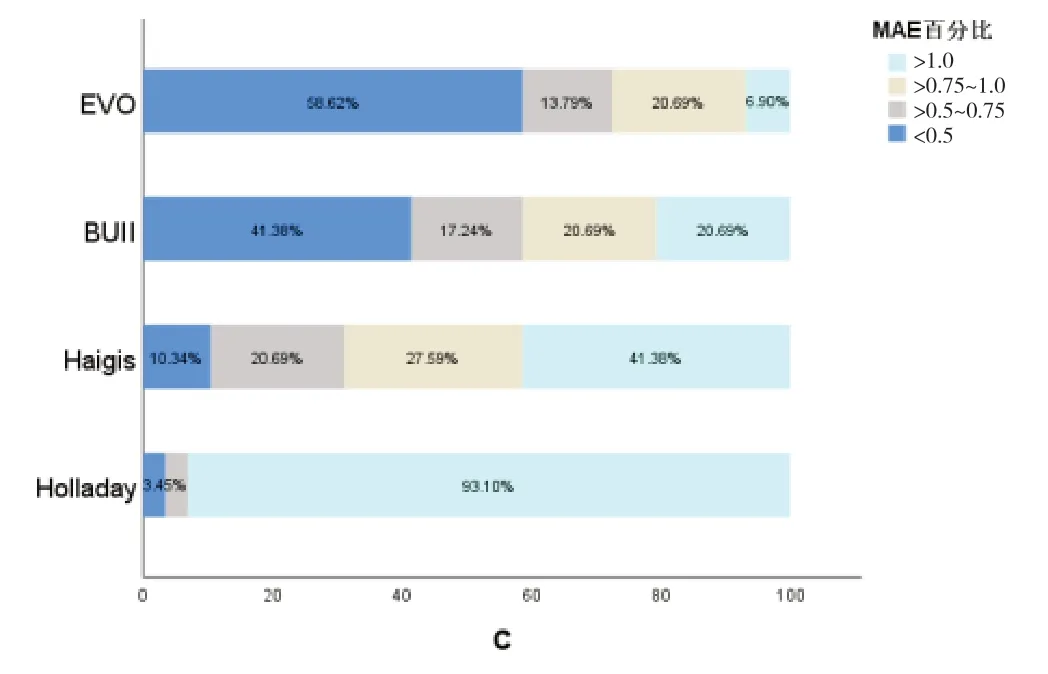
图4 四种公式MAE分别在不同屈光阈值范围内的百分比

2.6 MAE 与AL 的相关性 采用Spearman 秩相关分析显 示，MAEHolladay、MAEHaigis及MAEBUII的r＞0，P＜0.05，表明使用Holladay 公式、Haigis 公式和Barrett UniversalⅡ公式进行预测时，高度近视患者白内障术后的屈光误差与AL 呈正相关，即随AL 增长，Holladay 公式、Haigis 公式和Barrett Universal Ⅱ公式对术后实际屈光度的预测误差随之增大，预测准确性随之降低。MAEEVO的P＞0.05，表明EVO 公式的预测准确性受AL 影响不明显，其预测稳定性优于Holladay 公式、Haigis 公式和Barrett Universal Ⅱ公式，见表4。

表4 MAE与AL的相关性

3 讨论

本研究显示，在AL ≥26 mm 时，Holladay 公式较其他3 种公式的预测准确性差，且稳定性不佳，表明Holladay 公式不适用于高度近视患者IOL 的计算。Holladay 公式属于第三代IOL 计算公式，其对术后IOL有效位置（ELP）进行估算在第一代及第二代IOL 计算公式的基础上加用AL 和K 值。虽然早期研究显示Holladay 公式在高度近视患者IOL 计算中有良好表现［3-4］，但近期研究［5］表明，与Barrett Universal Ⅱ公式相比，高度近视患者使用Holladay 公式的准确性并不理想。这可能是由于Holladay 公式在计算中使用的数据较第四代及第五代IOL 公式少，故而准确性欠佳。

对Haigis 公式分析结果显示，Haigis 公式在AL ≥26 mm 时准确性高于Holladay 公式；在26 mm ≤AL＜28 mm 以及AL ≥30 mm 时准确性与Barrett Universal Ⅱ公式相似；但AL ≥28 mm 时，准确性较EVO公式差。这可能是由于Haigis 公式在IOL 计算上，除AL和K 值外，还引入了ACD、白到白（WTW）、晶体厚度（LT）等多组数据，且采用常数对ELP 进行估算［4］，通过线性回归对常数进行优化提高预测精度。CHEN 等研究结果也进一步证实这一结论［6］。然而，RONG 研究结果与本文有些差异，结果显示当AL＞30 mm 时，其准确性逊于Barrett Universal Ⅱ公式［7］，可能是由于Haigis公式受K 值影响较大。而Barrett Universal Ⅱ公式对ELP的计算增加为AL，K，光学ACD，LT 及WTW 水平等五个因素，可以精确估计ELP，从而提高对IOL 预测的准确性，故而普遍适用于各AL 情况下的IOL 计算，并在超长眼轴IOL 计算中也可保持良好的预测性［7］。

本研究显示，EVO 公式作为一个新的厚透镜公式，其准确性与Barrett Universal Ⅱ公式相当，且其90%以上的预测误差位于1.0D 以内，这与PANTANELLI 及GUO 的研究结果相符［8-9］。同时EVO 公式稳定性略优于Barrett Universal Ⅱ公式，这也验证了Lin 的结论［5］。这可能因EVO 公式使用AL、K 和ACD 作为预测因子的同时，为每只眼睛产生相应的“正视因子”［10］。但PEREIRA 的结论与本研究略有不同，针对高度近视白内障患者，Barrett Universal Ⅱ公式的稳定性及准确性优于EVO 公式［11］。原因可能是EVO 公式的准确性不仅受AL 及K 值影响，还受到a 常数的影响［12］，KHATIB等［13］认为通过适当的晶体常数优化，Barrett UniversalⅡ公式和EVO 公式的预测性能将同样准确。

EVO 公式不仅适用于高度近视患者，在其他类型特殊眼中的IOL 计算也有良好表现。MO 等［14］在2022年发表的一篇探讨ACD 对IOL 计算公式的影响研究中指出，EVO 公式针对浅前房患者有较为良好的准确性。HIPóLITO 等［15］认为在针对极端的ACD 或晶体厚度（LT）时，EVO 公式可获得更加可靠和稳定的结果。针对玻璃体切除术［16］、硅油填充术后或深板层角膜移植术后［17］发生白内障的患者，EVO 公式也十分适用。但对于EVO 公式是否适用于短眼轴患者尚存在部分争议［18-19］，仍需进一步探索。