基于机器视觉的插销自动装配算法研究
2023-06-09黄佳兴雷张文邓林志
黄佳兴,孙 晓,雷张文,于 柳,邓林志
(1.湖南工业大学 机械工程学院,湖南 株洲 412007;2. 株洲国创轨道科技有限公司,湖南 株洲 412007;3. 湖南工业大学 图书馆,湖南 株洲 412007)
0 引言
在“十四五”和《中国制造2025》等战略背景下,制造技术现朝着新型智能方向发展[1]。机器视觉技术作为一项新型工业生产中的辅助技术,随着智能化的发展得到了广泛的应用。
利用图像处理及机器视觉技术进行工业生产的最大特点,是能够快速无接触地获取目标信息[2]。在生产线上的应用可以有效避免人为主观性造成的误差;在新型工业生产线的应用中,装配视觉检测的机器人替代人工完成抓取和装配工作。装配生产线中因工件偏移造成的错误装配使得机器寿命缩短,而在工业传输链条的装配过程,对连接插销的准确插入有极高的要求,如果有偏差靠强行插入,会严重影响链条的使用寿命,因此及时反馈并更新工件位置信息是非常必要的。如何提高工件识别定位的效率与精度,一直是国内外学者的研究重点。
目前,在工件识别与定位中,图像处理、机器视觉、深度学习[3-5]等自动化识别处理方式被广泛应用。罗辉等[6]结合Hu 矩不变量和模板匹配方法对工件定位与识别,但是其结果的准确性对轮廓提取的精度有一定要求。龚海强等[7]通过比较两相邻点之间的高度差与欧氏距离大小关系,得出点间斜率,并以此确定工件位置,但是此方法要保证3 个相邻的采样点要在同一个区域内。武洪恩等[8]结合八邻域跟踪算法、Hu 矩、递进霍夫变换法,对工件完成了识别与定位。钟佩思等[9]将工件质心像素值作为样本点,通过对样本点进行正交函数拟合得到工件质心平面坐标,最后经双目视觉以工件质心进行三维重建。卢军等[10]通过加权最小二乘法拟合工件亚像素边缘的二维测量法来定位工件的策略,达到了工件亚像素级的定位精度。余永维等[11]利用GrabCut 算法、SURF 算法、视差测距法,实现了对目标工件图像的分离、三维立体匹配和定位。但是这些算法的计算量都较大,不适用于快速处理的场景要求。
综上所述,现有的工件检测算法存在算法复杂、对硬件设备要求较高、难以实时检测等缺点。针对上述问题,本文提出了一种快速的提取与调整策略,使其更易于在嵌入式设备上使用。
1 系统平台设置
1.1 系统平台搭建
该检测调整系统由图像采集系统、图像处理系统、机械系统、运动控制系统4 个子系统构成,如图1 所示。
图1 所示插销位置检测调整系统中,图像采集系统由200 万像素的CMOS 相机、畸变小于1.00%的定焦镜头和环形光源构成,镜头与光源同侧放置直射工件;机械系统由可自由移动的相机和光源支架构成;运动控制系统由移动滑台和舵机运动控制驱动器构成,树莓派(Raspberry Pi)与舵机运动控制卡控制舵机步进距离;图像处理系统基于OpenCV-Python平台搭建。移动滑台搭载相机与光源做同步移动。面阵CMOS 相机定距自动采集图像,并经由千兆网线传输到树莓派进行图像的保存与数据的处理。当一个目标插销被运送至检测点时,发出信号,相机获取当前图像,读取分析目标位置信息,并计算需要调整的角度,调整系统对插销进行调整,完成一个作业动作。
1.2 视觉系统标定
整个系统的坐标位置如图2 所示。
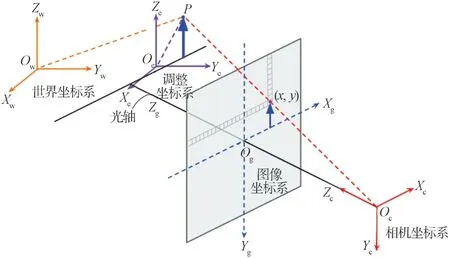
图2 各坐标系位置关系示意图Fig. 2 Position relationship of each coordinate system
图2 中,世界坐标系用{Ow-XwYwZw}表示、工件调整执行坐标系用{Oe-XeYeZe}表示、相机坐标系用{Oc-XcYcZc}表示、插销图像坐标系用{Og-XgYgZg}表示,根据式(1)可求解插销像素坐标(u,v)映射到{Oe-XeYeZe}坐标的变换矩阵T。
根据已知的像素坐标、图像坐标、相机坐标和执行坐标相互之间的坐标变换关系公式(2)
推导出如下像素坐标与末端执行坐标的映射表达式(3):
可得到变换矩阵T,
式(2)~(4)中:fx、fy为相机内参数中的焦距;u0、v0为相机感光板中心在像素坐标系下的坐标;R为外参数中的旋转矩阵;I为平移矩阵;f为像距;dx、dy为x、y方向上一个像素在相机感光板上的物理长度;以上参数可通过采集不同方向上的黑白棋盘格图像进行标定。
2 目标提取
为减轻后期计算压力,达到快速提取目标要求,在目标获取阶段需寻找一种准确有效的目标检测方法,将目标与背景剥离出来。
2.1 检测方法
在对目标进行识别前,需要从复杂的工业背景中检测到所需的目标并分离出来。在目标检测中,利用连续视频帧中目标区域的像素点变化可将目标从背景图像中提取出来。
根据检测目标背景的复杂程度以及相机的相对运动情况,不同的算法之间存在较大的差异。其中背景差分法、光流场法和帧间差分法是最常用于运动物体分离的方法[12]。为了提高工业生产线上的效率,快速提取目标并且读取目标信息。在上述3 种方法中,选用检测运动目标快速、检测精度较高、鲁棒性较好和计算资源需求较小的背景差分法。为进一步降低背景差分法的计算资源需求,提出对背景差分算法进行帧数获取的限制约束改进,即在连续的视频序列中只获取两张照片,不对中间图像进行计算处理,这样可有效提高计算效率。

图3 序列片段选取Fig. 3 Sequence fragment selection
2.2 快速目标提取
背景差分法被广泛应用于视频片段中的运动对象提取,根据视频帧之间的相减结果得到运动物体的变化来分离目标,原理如图4 所示。
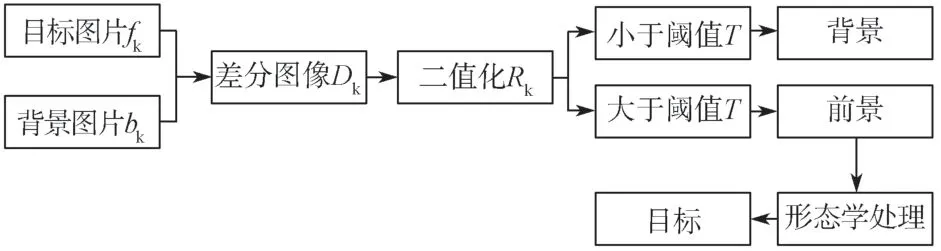
图4 背景差分原理图Fig. 4 Background difference schematic diagram
通过目标图像与背景图像得到的差分图像经阈值划分后得到最终运动目标,如式(5)所示。在对视频序列进行了精简化处理后,虽然降低了计算量,但是对提取结果有一定的影响。这些主要来源于环境变化带来的各种干扰,可以通过后续的图像增强处理予以消除。
式中:fk(x,y)为目标图像;bk(x,y)为背景图像;T为设定的阈值。
背景差分法需要建立一个背景图像,然后将目标图像与背景图像进行差分处理得到差分图像。本文选取了一个工序内的两张图像作为背景图像和目标图像进行处理。这两种图像是需通过快速筛选而决定的,整个过程如图5 所示。
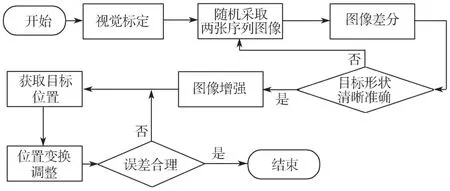
图5 目标快速提取调整流程图Fig. 5 Flow chart for target quick extraction and adjustment
当插销从流水线上过来时,相机捕获两张序列图像,对两张图像进行差分处理,通过将差分图像的像素点与预设好的阈值比较,判断像素点的分类情况,筛选出合格的目标图像。如目标图像不合格,则重复循环捕获序列图像,直至目标图像合格。经过快速背景差分处理后,剔除了目标外的大部分背景,图6为背景差分法处理后的图像及其像素灰度。
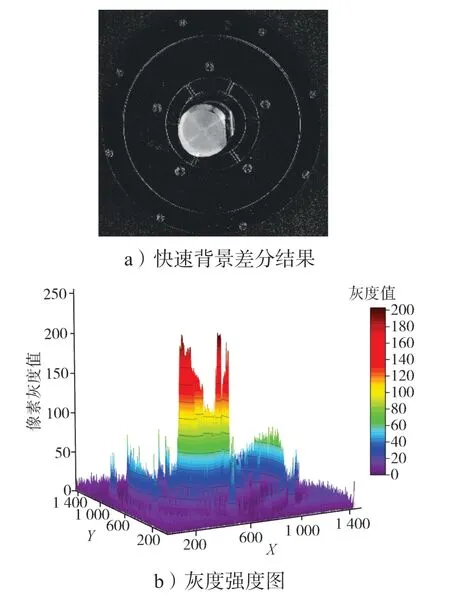
图6 干扰背景去除结果Fig. 6 Image after interference background removal
从图6 中可以看出,采用背景差分法处理图像,可以有效地分离出目标图像,但由灰度强度图可以看出还是存在许多干扰。
2.3 图像增强处理
为了削弱或者去除图像中的一些干扰信息,使图像的主体信息能够清楚地表示出来,需要对图像进行增强处理。考虑到本研究在消除噪点的同时,需要保护插销的边缘信息。因此在进行滤波和形态学处理时,对中心像素和边缘像素分别进行处理。对金属材质零件易反光的边缘处,进行了形态学腐蚀膨胀算法(morphology erosion-dilation algorithm,MEDA)来加强边缘特征。对中心和其他点附近的像素点,设置较大的权值并且灰度差值较小的双边滤波器来滤除图像的噪声,图7 为经过滤波和形态学处理后得到的图像。

图7 增强处理后的图像结果Fig. 7 Image after enhancement processing
2.4 特征提取
经过增强处理后的图像边缘特征变化最明显、差异最大的部分,通过图像梯度的变化,就能很好地找到图像边缘。目前常用的检测算子有Canny、Sobel、Scharr 等,图8 所示为插销在不同的检测方法下获得的边缘检测效果图。
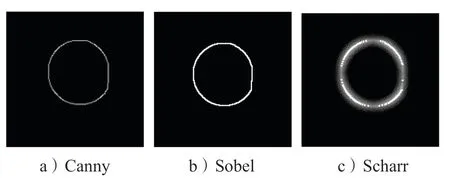
图8 边缘检测效果对比图Fig. 8 Edge detection effect comparison chart
对此图8 中3 种算子的边缘检测效果图,可以看出,Canny 算子的边缘检测效果较好。
3 目标位置调整
目前,关于目标位置的获取,一般运用霍夫变换(Hough)或者其他智能匹配算法和来实现,但是传统的霍夫变换所需计算资源极大,难以满足快速检测的需求。
3.1 基于粒子群优化的Hough 变换
对于简单几何形状的图像边界的提取,霍夫变换是一个非常直接有效的方法。其首先通过将图像坐标上每一点映射成参数坐标下的对应曲线,然后利用投票算法机制,统计在参数坐标下对应曲线相同交点的个数,并且根据结果的局部最大值,得到检测图像中的特征曲线[13]。
如关于直线的检测,在直角坐标下的直线上的一点,经霍夫变换后,为极坐标下的一正弦曲线,多个点则对应多条曲线。如果通过一个交点的曲线越多,则表示原直角坐标系下的点在同一条直线上。此时两曲线交点坐标即原直线的两个极坐标参数ρ和θ,且满足
曲线霍夫变换过程如图9 所示。
虽然霍夫变换能准确地提取到所需的特征曲线,但由于图像的像素数量较大,导致所需的计算量较大,内存占据较多,检测耗时严重,无法满足实时处理的问题。为此,在传统的Hough 变换中加入粒子群优化算法。把粒子群算法中的粒子位置和适应度值替换为Hough 变换中解出的参数和累加数组值。通过适应度值更新粒子速度和位置,并在下一代中剔除适应度值低的粒子,以此降低算法的计算量,提高处理速度。
其中粒子群算法可以描述为在n维解空间中,用xi=[xi1,xi2, …,xin]表示粒子i的当前位置;用vi=[vi1,vi2, …,vin]表示粒子i的当前飞行速度。找到粒子i所经历的最好位置pi=[pi1,pi2, …,pin],pi也称个体最好位置;最终得到所有粒子经历的最好位置pg=[pg1,pg2, …,pgn],也称全局最优位置。
粒子群算法的速度和位置更新公式如下:
式(7)中:rand1、rand2是两个0~1 间的随机数;c1、c2为学习因子,设为常数2;w为惯性因子,其中w=1.5Mk/kM,其中Mk为第k次迭代时粒子群的数量;M为初始粒子量。
通过适应度更新每个粒子的位置pi(k+1),即
以检测直线的过程为例,具体说明结合了粒子群优化的Hough 变换算法过程:
1)选择1 个具有m个粒子的种群S(0),设置初始种群S(0)={P1,P2, …,Pm},初始极坐标参数ρ和θ为ρ0、θ0,初始累加数组A为0;
2)对预处理后的图像进行边缘提取后得到目标边缘点集合;
3)随机挑选点集中两点Pp1、Pp2,构建直线并获得直线极径和极角,用该数据对粒子位置进行设置,直到所有粒子完成初始化设置;
4)随机设置每个粒子在种群中的初始速度vi;
5)利用适应度函数,计算粒子的适应度值f(xi(k,ρk,θk));
6)根据式(9)比较每个粒子位置的当前适应度值和历史最优适应度值,将当前最优适应度值的粒子位置设为全局最佳位置,并更新粒子位置;
7)选取适应度值大的粒子组成下一代粒子群;
8)根据直线参数方程更新k+1 代种群S(k+1)中每个粒子的速度vi(k+1,ρk,θk);
9)更新k+1 代种群中粒子的位置;
10)返回第5 步,重复执行,直到迭代结束。
3.2 目标位置信息的获取
对于大部分零件的二维图像都可以拆分成直线和圆弧这样的简单几何形状,对此可以通过粒子群优化的霍夫变换算法来检测形状特征进行插销位置的确定。因此本文提出了一种通过拆分零件图像特征的目标位置获取方法。只检测图像的某些几何形状特征,以加快检测的速度。计算插销旋转角度的具体步骤如下:
1)通过Hough 变换找出图像中直线段,设置最大阈值得到所需的直线L,完成直线提取;
2)利用Hough 变换,找出图像中第二个形状特征圆,进行中心定位,得到原本的插销圆的中点(xr,yr);
3)用最小包围矩找出包围零件的最小矩形,得到最小包围矩的中心点坐标(xe,ye);
4)对插销旋转角度大小进行计算。为统一方向,选取直线在X方向上值最小的点作为直线L的计算起点,使得直线L与X的夹角
根据式(12)计算
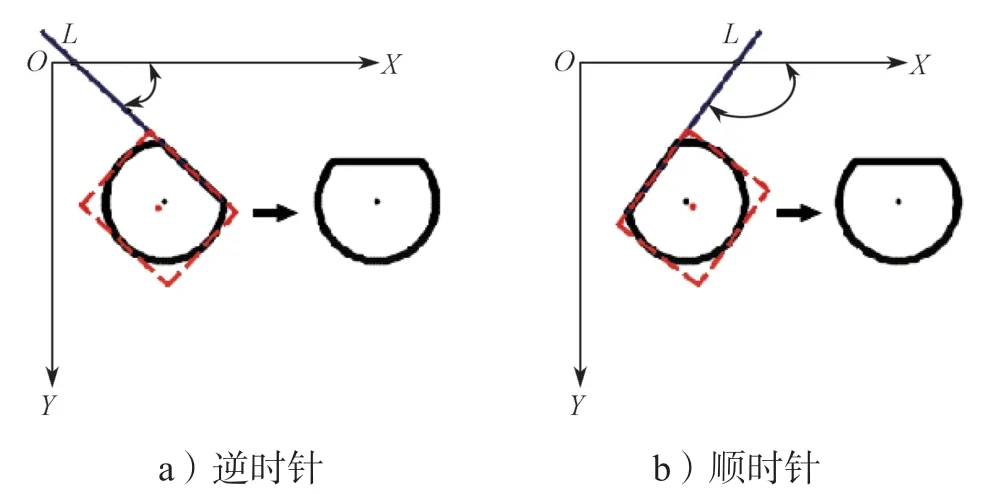
图10 旋转方向示意图Fig. 10 Rotation direction diagram
最后对旋转后的插销角度位置进行校验。根据计算出的图像旋转偏移量Δθ旋转图像,再次计算图像中直线L与X的角度,确定旋转角度的误差是否符合要求。
通过插销像素坐标变化可计算出插销的位移。已知目标插销中心像素坐标为(u1,v1),标定插销中心像素坐标为(u2,v2),则插销在图像坐标系下的移动量为(u2-u1,v2-v1)。利用式(14)计算出像素偏移量∆u、∆v,式(9)将∆u、∆v转换为执行坐标系下的偏移量∆x、∆y。
4 仿真实验
为减少在实际测量中的误差,在SolidWorks软件中将待调整插销角度位置随机摆放,通过比较本文算法计算出的插销旋转角度偏移量Δθ。和SolidWorks 中实际测量的角度偏移量Δθ*,得到实际的误差结果。此外,为了评估本文方法和其他方法在求解旋转角度时的精度和速度,与Hough、SIFT、ORB 算法进行对比。总共进行了50 次模拟实验,图11 所示为本文算法的部分结果。

图11 部分仿真实验结果图Fig. 11 Partial simulation experiments
用式(16)计算偏移量的误差δθ和δθ´将算法独立运行后,两种算法所得的误差角度和运行时间的对比曲线如图12~13 所示。
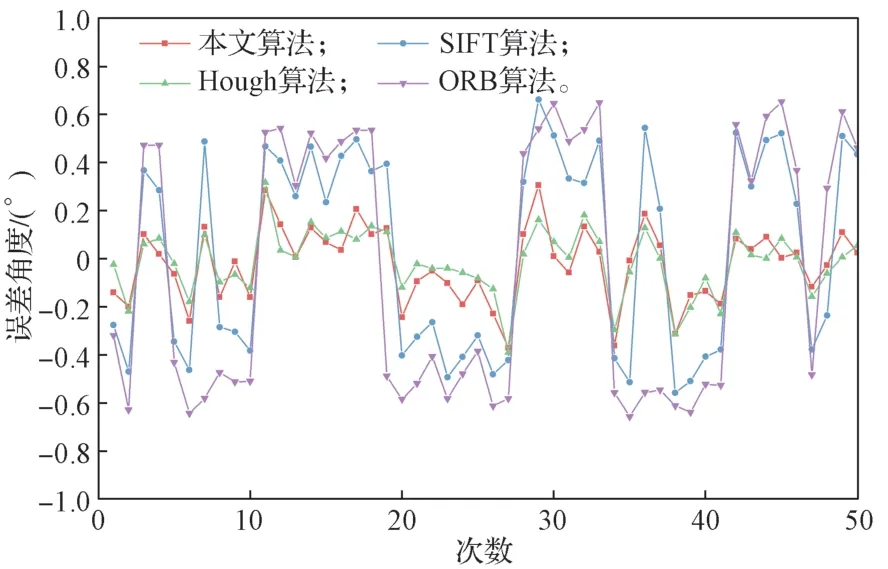
图12 角度误差对比曲线Fig. 12 Angular error comparison curves
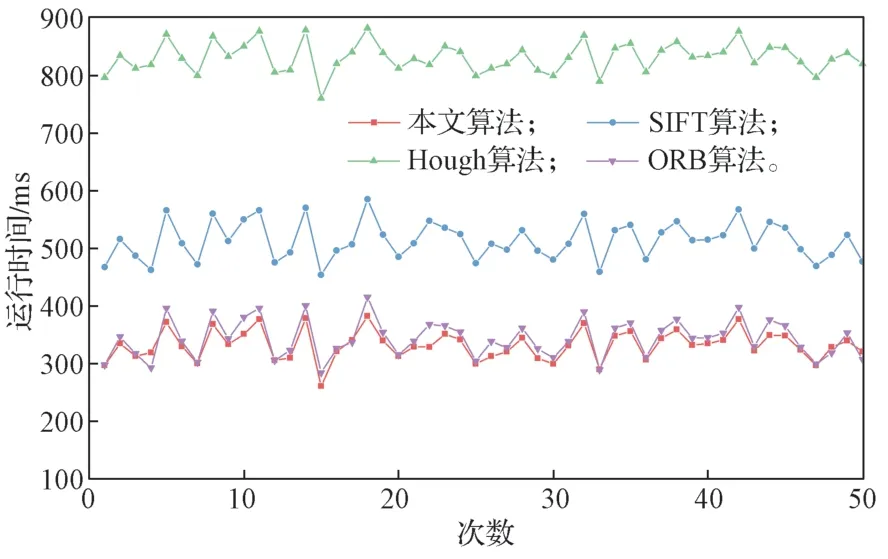
图13 运行时间对比曲线Fig. 13 Runtime comparison curves
对比图12 中各算法的角度误差曲线,可以看出本文算法和Hough 算法的计算测量误差范围为[-0.4°,+0.4°],SIFT 算法的误差范围为[-0.6°, +0.6°],ORB算法的误差范围为[-1°, +1°]。4 种算法在插销调整中计算的角度误差均小于1°,满足基本误差范围要求,但是SIFT 算法和ORB 算法的计算误差波动较大,且利用ORB 算法时还出现了误差角度方向的错误。本文算法在对Hough 算法进行精简后,仍然可以保持同样的精度,且在求解旋转角度时的精度要明显高于其他两种算法的对应值。
对50 次实验的运行时间进行统计,得到本文方法对旋转角度进行计算的平均时长约为332.0 ms,SIFT 算法所用平均时长约为512.6 ms,Hough 算法所用平均时长约为831.7 ms,ORB 算法所用平均时长约为343.2 ms。可以利用本文方法计算的运行时间较其他3 种方法有所缩短,提高了工作效率。
综上所述,通过对霍夫变换中引入粒子群算法,在保证霍夫变换的精度情况下可缩短运行时间,提高了插销位置匹配的速度。
5 结语
为了精确且快速获取流水线上随机摆放的插销位置信息,本文提出了一种快速的目标提取与调整策略。运用了一种基于背景差分的目标背景分离和粒子群优化Hough 变换的定位算法。在背景分离中,为节省嵌入式设备的计算资源,对帧数获取进行限制约束。通过获取其中几张图像代替整个视频帧的方法减少了图像处理环节的计算量,提高了计算速度。在特征提取与匹配中,通过拆分图像几何形状特征进行目标匹配,精简了特征数量,从而提高了运算效率,并且具有较高的精度。结合粒子群优化的霍夫变换,通过丢弃劣等种群来加快传统霍夫变换的计算速率。相比其他方法,本文方法也更能满足使用嵌入式设备的工业自动化生产需求。
