基于双边闭环函数的T-S 模糊模型非线性系统网络跟踪控制
2023-06-09肖会芹徐春秀黄浪尘曾红兵彭天顺
肖会芹,徐春秀,黄浪尘,曾红兵,彭天顺
(湖南工业大学 电气与信息工程学院,湖南 株洲 412007)
1 研究背景
近几十年来,因实际工程需要使得非线性系统稳定和综合问题的研究受到了大量学者的关注。而Takagi-Sugeno(T-S)模糊模型[1],因其对非线性系统优越的逼近特性,降低了非线性系统的分析难度,成为非线性系统建模和控制的强有力工具。于是大量基于T-S 模糊模型的非线性系统问题被科研工作者们研究,如稳定性问题[2]、鲁棒耗散控制问题[3]、滤波器设计问题[4]、滑模控制问题[5],以及跟踪控制问题[6]等。
跟踪控制的主要目标是设计一个跟踪控制器,使被控对象输出或状态在一个小的误差范围内跟踪给定参考信号[7]。跟踪控制在现代工业中的应用非常普遍,如路径跟踪[8]、轨迹跟踪[9]等。因为非线性系统跟踪控制问题相较于稳定性问题更为复杂,也更具有挑战性,从而成为当下的研究热点之一。
网络的快速发展、网络节点硬件成本的不断降低,也使得网络被广泛地应用到非线性系统的跟踪控制中[8-15]。但是在实际网络控制系统中,网络通信带宽有限,这会使得网络系统产生信号传输时滞、数据包丢失等现象,这在一定条件下会显著降低系统性能,甚至影响系统的稳定性。因此,目前非线性系统的网络跟踪控制也引起了许多学者的关注。文献[11]在变采样周期情况下,为提高带宽利用率,提出了一种事件触发方案,研究非线性网络控制系统输出跟踪控制问题。文献[15]中提出将定采样周期、数据传输时滞和数据丢包统一转化为零阶保持器端数据更新周期,通过求解零阶保持器端最大数据更新周期,研究了考虑网络诱导和丢包的非线性系统网络跟踪控制问题。虽然上述文献都取得了一定的研究成果,但是没有充分利用采样区间的信息,这使得结果仍然存在一定的保守性。
近年来,很多学者基于输入时滞方法[16]提出了新的分析方法。如不连续L-K(Lyapunov-Krasovskii)泛函方法[17],时间依赖离散型Lyapunov 泛函方法[18],闭环Lyapunov 泛函方法[19],双边闭环函数方法[20]等。其中,由于双边闭环函数方法包含[tk,t]和[tk,tk+1)采样区间信息,且只要求Lyapunov泛函在采样点大于0。这给Lyapunov 泛函的构建带来更多的自由度,使其被越来越多的学者使用[21-25]。如文献[21]通过分割采样区间来构造新的双边闭环Lyapunov 泛函,进而得到改进的稳定性判据。文献[25]利用双边闭环函数方法,研究了数据通信时延环境下采样控制系统的稳定性问题。
基于上述双边闭环函数的思想,本文拟在T-S 模糊模型非线性系统网络跟踪控制中,引入一个新的双边闭环泛函,用以研究考虑网络诱导时滞和数据丢包环境下,该类系统的H∞跟踪控制问题。这种双边闭环函数在泛函构造中考虑了系统采样区间[tk,tk+1)的信息,因而使得积分不等式的向量和状态向量紧密耦合。且其充分利用了有关实际采样的区间结构特征信息,并且使用自由权矩阵积分不等式来进一步降低系统的保守性,得到了基于线性矩阵不等式(linear matrix inequality,LMI)的跟踪系统稳定性判据。最后,通过一个实例进行仿真,验证了所提出设计方法的有效性和优越性。
本文采用如下标号:上标“-1”和“T”分别表示矩阵的“逆”和矩阵的“转置”;Rn表示n维欧几里得空间;Rm×n代表m×n维的实矩阵;p>0表示矩阵是正定的;diag{…}表示块对角矩阵;“*”表示对称矩阵中的对称项;I和0 分别代表合适维度的单位矩阵和零矩阵;;。
2 问题描述



3 主要结果及证明


4 数值实例

由表1 可以得出,定理1 明显改进了文献[7]和[15]的结果。

表1 不同方法的最大输入时滞结果Table 1 Maximal input delay of different methods
对于模糊控制器未知的情况,在式(11)中设定Qg=I、ρ=2。在相同的条件下,比较不同方法的跟踪性能:
1)采样器的采样周期Ts=10 ms;
2)信号传输时滞τ=40 ms;
3)数据包丢失个数γ=1。
由定理2 可以得出δ1=1、δ2=1 时的模糊控制器K1=K2=[-28.782 5 -16.991 9],文献[15]中给出的模糊控制器K1=K2= [-20.742 2 -7.953 8]。假设初始状态为x(0)=[2 -1]T,xr(0)=[-1 1]T。两个状态变量的跟踪误差曲线如图1 所示。由图1 可以看出,在相同网络条件下,相较于文献[15],本文所设计的模糊控制器产生的跟踪误差明显更小,即本文所设计的控制器有更好的跟踪控制效果。由表1 也可以得出,对于给定的模糊控制器,本文提出的方法,在相同的H∞跟踪性能要求下,比文献[7]和[15]具有更大的输入时滞上界,这表明本文给出的方法相较于已有方法,保守性更低。
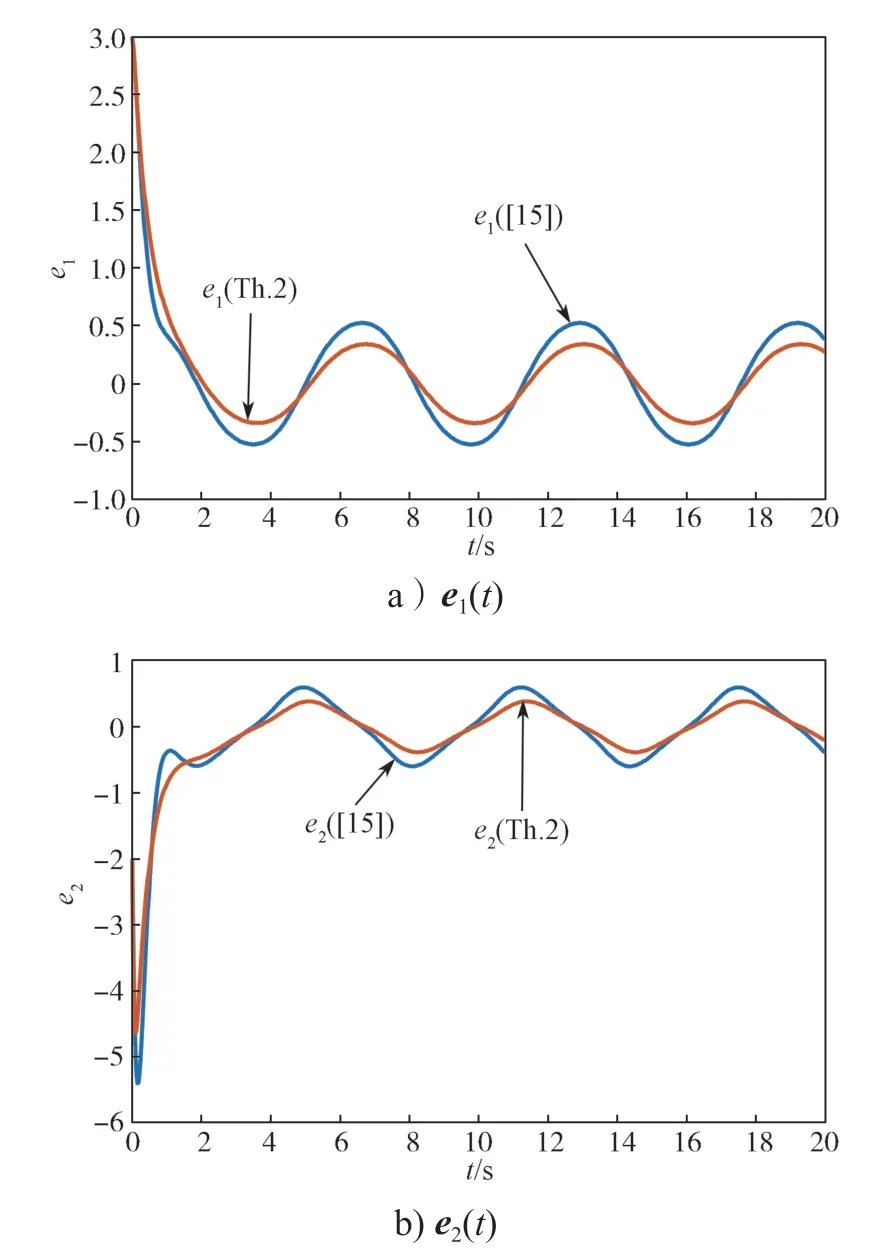
图1 e(t)跟踪误差曲线Fig. 1 Tracking error curves of e(t)
5 结语
本文研究了一类具有数据丢包和传输时滞的非线性系统H 网络跟踪控制问题。首先基于T-S 模糊模型建立非线性系统跟踪误差模型,在此基础上构造了一个新的双边闭环函数,这种双边闭环函数充分利用了有关实际采样的区间结构特征信息,在考虑网络诱导时滞和数据丢包环境下,获得模糊控制器增益已知和未知情况下实现系统跟踪控制更低保守性的充分条件,然后采用参数调整法获得跟踪效果更好的模糊控制器参数,最后通过一个Duffing 强制振荡系统的仿真实例验证了本文方法的有效性。
