随机过程中的随机变量概念错误及纠正
2023-06-09高宏
高宏

[摘 要]文章以维纳过程定义为例,分析随机过程理论在研究单个质点随机运动时,将质点位移与时间之间的数量关系抽象为随机变量的基本概念错误,以及使用描述大量质点空间位置分布的随机变量数字特征来刻画单个质点位移随时间变化规律的方法错误。文章将布朗粒子位移与时间之间的数量关系还原为时间函数,根据爱因斯坦“同一个布朗粒子在不同微小时间间隔中的运动相互独立”的基本假设,从理论上证明了布朗运动的瞬时速度为白噪声过程,并基于白噪声样本函数重新定义了维纳过程,建立了可正确描述单个布朗粒子运动规律的样本函数模型。
[关键词]随机过程;随机变量;样本函数;维纳过程
[中图分类号] G644.5 [文献标识码] A [文章编号] 2095-3437(2023)02-0052-05
随机过程理论是一种利用数学基础理论和研究方法,探讨和揭示客观世界动态随机现象数量关系及其变化规律并解决自然科学、工程技术和社会科学等领域实际问题的应用数学理论。随机过程理论最早源于爱因斯坦1905年对布朗运动的定量研究,随机过程、随机变量和样本函数等数学概念是从质点随机运动现象中抽象出来的一种数学结构,是人脑对质点随机运动现象数量关系及空间形式的思维反映。随机变量基本概念虽然远离了直观的经验世界,却能更深刻地反映随机现象的本质。由于随机变量定义及基本概念的抽象性和复杂性,维纳(Wiener)在研究单个布朗粒子所走曲线的数学性质时,将单个布朗粒子的位移与时间之间的数量关系抽象为随机变量[1-4],无形中改变了布朗粒子位移函数的定义域和值域,导致研究对象从单个质点改变为质点集合,并用随机变量的统计特性来描述样本函数的曲线性质,从而得出了“布朗粒子位移服从正态分布”“布朗粒子位移与时间的平方根成正比”和“布朗运动路径处处不可导”等一系列与物理学理论和实验结果严重不符的结论,为自然科学、工程技术和社会科学提供了错误的理论、方法及工具。
本文拟分析维纳过程定义中的基本概念错误和研究方法错误,基于爱因斯坦“布朗粒子在不同时间间隔中的运动相互独立”的基本假设,推导出布朗粒子的瞬时速度为白噪声过程,利用白噪声样本函数重新定义维纳过程,建立可正确描述单个布朗粒子运动规律的数学模型。
一、概率论中的随机变量定义
随机变量是概率论中一个极为重要的基本概念,也是研究隨机现象的基本工具。引入随机变量的主要目的是把随机试验的结果数量化,将随机事件的结果映射为实数,这样就可以利用数学分析方法来研究随机现象。
随机变量的定义涉及随机试验、样本点和样本空间三个基本概念。
随机试验是指人们对随机现象进行的观察或观测,随机试验具有以下三个特征:
(1)可重复性:在相同条件下可重复进行。
(2)多结果性:试验结果不止一个,但所有可能的结果都是事先明确可知的。
(3)不确定性:每次试验之前不能确定会出现哪一个结果,但可以肯定会出现所有可能结果中的一个。
尽管一次随机试验将要出现的结果是不确定的,但其所有可能结果是明确的。我们把大量重复随机试验会出现的每一种可能的结果称为一个样本点,一般记为ω;全部样本点的集合称为样本空间,一般记为Ω。
定义:设随机试验的样本空间为Ω={ω},若X(ω)为定义在样本空间Ω上的单值实数函数,则称X(ω)为随机变量,简记为X。
随机变量的取值可以是连续的,也可以是离散的,根据随机变量取值的不同,可以分为连续型随机变量和离散型随机变量。
通常用大写英文字母X,Y,Z,…来表示随机变量,用小写英文字母x,y,z,…表示实数。如果随机试验的结果本身就是一个实数x,即样本点ω本身是一个实数,这时常定义X= X(ω)= ω= x。
对于抛硬币试验,试验结果可能是硬币正面向上,也可能是硬币反面向上,即有两种可能的结果,而且只有这两种结果,事先可以明确。因此该试验所对应的样本空间Ω由ω1和 ω2两个样本点构成,我们指定实数1和-1分别与样本点ω1和 ω2对应(见图1),则随机变量可写成
[X=Xω= 1,ω=ω1-1,ω=ω2 (1)]
从上述随机变量的定义可以看出,随机变量X的取值由样本点ω决定,也就是说,随机变量X是样本点ω的函数,即有X= X(ω)。因此,随机变量的定义域为样本空间Ω。
随机变量实质上是一个定义在“随机试验所有可能结果集合”上的单值实数函数,随机变量的不同取值与随机试验的所有可能结果一一对应,随机变量的值随试验结果的不同而变化。从数学上讲,随机变量就是一个从随机试验结果的集合到实数集的映射。
二、随机过程与随机变量的关系
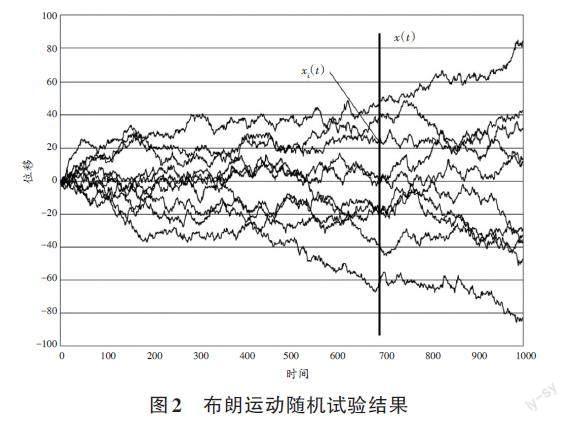
在现实世界中,许多随机现象都是随着时间的进程变化发展的,这类动态随机现象就是所谓的随机过程。例如在相同条件下重复10次观察一个从原点出发的布朗粒子位移x随时间t的变化过程,可得到如图2所示的10条布朗粒子位移曲线,这10次测量结果也可分别用10个时间函数x1(t),x2(t),…,x10(t)表示。尽管每次的试验结果各不相同,但每次的结果却是一个确定性的时间函数xi(t)。若同时观测10个从原点出发的布朗粒子位移x随时间t的变化过程,也会得到与图2类似的试验结果曲线。
显然,每个布朗粒子的观测结果,均为一个随时间变化的实数,亦即随机过程的试验结果是一族时间函数x1(t),x2(t),…,xi(t),…,也就是说,随机过程试验的样本点ωi与时间函数xi(t)一一对应(见图3)。
由于随机过程的试验结果是一族时间函数,因此我们可用定义在Ω×T上的二元函数X(ω,t)来描述随机过程的所有试验结果。下面给出X(ω,t)在四种不同情况下的含义:
(1)固定ω,X(ω,t)是一个自变量为t、定义域为T的普通函数,它是一次随机过程试验(即在T上进行一次全程观测)所得到的一条记录曲线或一个时间函数x(t),通常称为随机过程的一次物理实现或一个样本函数(轨道)。样本函数x(t)是确定性的时间函数,从时间角度刻画了随机过程。
(2)固定t,X(ω,t)是一个定义在样本空间Ω上的单值实数函数,也就是概率论中的随机变量,简记为X(t)。从概率论的观点来看,随机过程就是一族有时间标记的随机变量X(t)。随机变量X(t)从空间角度刻画了大量布朗粒子在某一时刻的位置分布规律。
(3)固定ω,固定t,X(ω,t)是一个实数,表示某次随机过程试验在t时刻的观测值。
(4)当ω和t均变化时,随机过程试验的所有结果构成一族样本函数,因此,所有这些样本函数的总体或集合就构成了随机过程。
综上所述,我们可以从两个不同的角度给出随机过程的两种等价定义。
定义1:随机过程是一族依赖于样本空间的时间函数集合。
定义2:随机过程是一族依赖于时间的随机变量集合。
定义1把随机过程看成是一族样本函数的集合,这是概率论随机变量定义的推广。概率论将样本空间中的样本点映射成实数轴上的一个点,而随机过程则是将样本空间中的样本点映射成一个时间函数(随时间变化的实数)。
定义2把随机过程看成是概率论中多维随机变量的推广,可以把多维随机变量的理论作为随机过程理论的基础。
以上两种定义从不同的角度描述了随机过程,其本质是相同的,互为补充。在工程技术领域对随机过程做实际观测常用定义1,观测次数越多,所得样本函数数量也越多,则越能掌握随机过程的统计规律。定义2与概率论中的随机变量定义相联系,因此在数学领域做随机过程理论分析时,常用定义2。时间分割越小,多维随机变量的维数n就越大,也就越能细致描述随机过程的统计规律。
在实际应用中,样本函数x(t)用来记录或描述一个质点的位移随时间的变化过程,随机变量X(t)则用来描述大量质点在某一时刻的空间位置分布。所有质点在t时刻的位置,或所有样本函数x(t)在t时刻的函数值,就是t时刻随机变量X(t)的取值。
随机变量符号X(t)并不表示X(t)是时间t的函数,X(t)是定义在样本空间Ω上的单值实数函数,它只表示t时刻所有样本函数的取值,即X(t)={ x1(t),x2(t),…,xi(t),…}。但是在随机过程理论中,却出现了用随机变量X(t)来描述单个质点位移x(t)的基本概念错误,无形中改变了样本函数x(t)的定义域和值域,导致研究对象从单个质点改变为大量质点,从而得出了一系列与事实不符的错误结论。
三、各态历经随机过程
研究随机过程的统计特性,从理论上说需要通过实验观测得到所有样本函数x(t),然后才能用统计方法求出不同时刻随机变量X(t)的数学期望、方差和自相关函数等数字特征,但这在实际研究工作中往往办不到,因为这需要对一个随机过程进行大量重复的实验或观察,甚至需要实验次数N趋于无穷大时才能满足要求。
有一种平稳随机过程,对其任何一个样本函数x(t)所做的各种时间平均,从概率意义上趋近于随机变量X(t)的各种统计平均,则称之为具有各态历经性的随机过程。
各态历经随机过程的任何一个样本函数x(t)都经历了随机过程X(ω,t)的所有可能状态,因此可用任何一个样本函数x(t)的时间平均来代替X(t)的统计平均或集合平均,简化随机现象的测量和计算过程,给解决实际问题带来极大的方便。
例如,分析电子产品中的白噪声时,用常规方法,需要在同一条件下,同时测量并记录所有电子产品中的白噪声电压或电流波形,再用统计方法计算出白噪声过程的均值、方差和自相关函数等数字特征。而利用白噪声过程的各态历经性,则只需要在同一条件下,长时间测量并记录一台电子产品的白噪声,然后用求时间平均的方法,即可获得白噪声过程的均值、方差和自相关函数等数字特征,大大简化实际问题的研究过程。
对于随机游走和布朗运动这类非平稳随机过程,各个样本函数具有不同的上升或下降趋势,整个过程不具有各态历经性。因此,研究随机游走和布朗运动的随机变量和样本函數时,要分别采用概率分析方法和函数分析方法来研究它们的空间统计特性和时间变化规律。
四、维纳过程定义的概念错误分析
维纳过程是随机过程理论中一种重要的连续时间随机过程,是刻画一系列复杂随机过程的基本工具。维纳过程不仅在随机过程理论中占有相当重要的地位,而且也是自然科学、工程技术和社会科学研究动态随机现象的重要数学工具。液体中悬浮微粒的布朗运动、光纤陀螺中的随机游走误差和股票市场中的价格波动等随机现象均可用维纳过程进行描述。
(一)爱因斯坦布朗运动理论
布朗运动是物理学中的一个著名现象。爱因斯坦于1905年首先对布朗运动进行了定量研究,为随机过程理论的建立和发展奠定了基础。
由于宏观可观测物理量与大量微观粒子运动的统计规律有关,因此爱因斯坦的研究对象并不是一个布朗粒子,而是由大量粒子组成的热力学系统,爱因斯坦关注的是大量布朗粒子在某一时刻的空间位置分布规律。
爱因斯坦认为布朗粒子的随机运动是由于受到大量液体分子的高速碰撞而引起的,并提出了“同一个布朗粒子在不同微小时间间隔中的运动相互独立”和“不同布朗粒子之间的运动相互独立”两个假设。
爱因斯坦对一维布朗运动进行了定量研究,假设所有布朗粒子同时从x轴的原点出发,根据热分子运动扩散方程推导出了大量布朗粒子在t时刻空间位置的概率分布函数
式中D为扩散系数。
显然,所有布朗粒子在t时刻的空间位置服从数学期望为零、方差为2Dt的正态分布。图2所示的布朗运动仿真试验结果也表明,大量布朗粒子在某一时刻的空间位置服从正态分布,其方差与时间成正比。
(二)维纳过程定义
维纳在研究爱因斯坦布朗运动理论后,发现爱因斯坦仅从统计的角度成功地解释了大量布朗粒子的扩散现象,但是并没有给出单个布朗粒子的运动学描述。
维纳对单个布朗粒子运动轨迹的数学性质感兴趣,首先设X(t)为布朗粒子在t时刻的位移[1-4],然后根据爱因斯坦的“同一个布朗粒子在不同微小时间间隔中的运动相互独立”假设和大量布朗粒子在t时刻的位置服从正态分布的结论,给出了如下的维纳过程定义:
若一个随机过程{ X(t),t≥0}满足
(1)X(t)是独立增量过程。
(2)X(t)~N(0,σ2t)。
(3)X(t)关于t是连续函数。
则称X(t)是布朗运动或维纳过程。
(三)维纳过程定义中的概念错误
维纳过程首先用X(t)表示一个布朗粒子在t时刻的位移,因此X(t)是定义在时域T上的一般函数,表明X(t)只是随机过程X(ω,t) 固定ω时的一个样本函数x(t),映射的是样本空间Ω中的一个样本点,亦即布朗运动的一次试验结果。
维纳过程在定义中又假定X(t)为服从正态分布的随机变量,表明X(t)是定义在样本空间Ω上的函数,也就是t时刻的随机变量,映射的是样本空间Ω上的所有样本点,亦即布朗运动的所有试验结果。
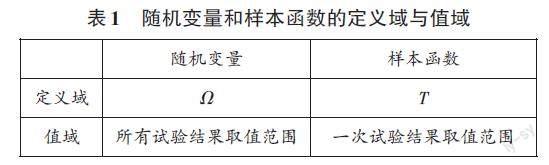
随机变量和样本函数是两个具有完全不同定义域和值域的函数(见表1),描述的是完全不同的随机现象。维纳过程定义使用同一函数符号X(t)来表示样本函数和随机变量,从根本上混淆了样本函数和随机变量所表达的内涵和外延。
维纳过程的研究对象是一个布朗粒子在t时刻的位移X(t),因此X(t)是时间t的一般函数。但是维纳过程定义却将X(t)又当作随机变量,无形中改变了X(t)的定义域和值域,导致研究对象从单个质点改变为质点集合,加之用爱因斯坦描述大量布朗粒子空间位置正态分布的统计特性来刻画单个布朗粒子的位移性质,势必会得出一系列与事实不符的错误结论。
五、维纳过程性质与事实不符
维纳过程将单个布朗粒子在t时刻的位移X(t)当作随机变量,改变了时间函数X(t)的定义域和值域,从而得出“布朗粒子位移服从正态分布”“布朗粒子位移与时间的平方根成正比”和“布朗运动路径处处不可导”等一系列与物理学理论和实验结果严重不符的结论。
(一)正态分布假设与经验事实不符
假设布朗粒子位移X(t)服从(0,σ2t)正态分布,根据正态分布的性质,布朗粒子位移曲线X(t)应具有如下两个特点:
(1)对称性:在每一时刻t,绝对值相等的正、负位移出现的次数大致相等。
(2)集中性:在每一时刻t,布朗粒子在0点附近出现的次数最多。
根据维纳过程定义X(t)关于t是连续函数的性质,可画出维纳过程描述的布朗粒子位移曲线(见图4)。
显然,维纳过程描述的布朗粒子位移曲线与图2所示的布朗粒子位移曲线完全不符。图2所示的布朗粒子位移曲线均随时间向远离原点的方向持续扩散,既不呈现正态分布的对称性,也不具有正态分布的集中性。
事实上,爱因斯坦关于“布朗运动服从正态分布”的结论指的是大量布朗粒子在某一时刻的空间位置服从正态分布。观察图2所示的布朗粒子位移曲线可以发现,所有布朗粒子在同一时刻的位置均服从正态分布,并具有正态分布的对称性和集中性。
(二)路径处处不可导性质与物理学实验不符
维纳基于“布朗粒子位移服从正态分布”的假设,还得出了“布朗运动路径处处不可导(瞬时速度无穷大)”的著名论断,并认为测量布朗粒子“瞬时速度”的任何努力都是徒劳的。
2010年,美国得克萨斯大学的李统藏成功地利用激光光镊技术首次实验测量到了布朗粒子的瞬时速度,实验结果证明了单个布朗粒子的瞬时速度波形为白噪声[5],表明布朗运动的导数(瞬时速度)不仅存在,而且可观测。
李统藏的研究成果在《科学》杂志上发表后,在全球引起了极大的轰动。《科学》杂志将李统藏的布朗粒子瞬时速度测量实验推荐为大学及高中教学内容,美国明尼苏达大学等学校的相关课程已经将该实验作为教学內容。
六、重新定义维纳过程
(一)布朗运动瞬时速度
设x(t)为布朗粒子在t时刻的位移,根据爱因斯坦“同一个布朗粒子在不同微小时间间隔中的运动相互独立”假设,可知单个布朗粒子的瞬时速度v(t)在不同时刻互不相关,因此v(t)的自相关函数可表示为
[Rvτ=vt-τv(τ)=N0δτ (3)]
式中τ为时间间隔,N0为正实常数,δ(τ)为单位冲击函数。
根据维纳-辛钦定理,平稳随机信号的功率谱密度是其自相关函数的傅立叶变换,v(t)的功率谱密度
[Svf=-∞∞v(t)e-j2πftdt=N0 (4)]
即单个布朗粒子的瞬时速度v(t)的功率谱密度在整个频率轴上均匀分布。
式(3)和式(4)表明v(t)为平均功率为N0的白噪声,与李统藏的布朗粒子瞬时速度测量实验结果完全相符。
(二)重新定义维纳过程
由于单个布朗粒子的瞬时速度v(t)就是单个布朗粒子位移x(t)的导数,白噪声的平均功率N0等于其方差σ2,因此,可给出如下的维纳过程定义:
若n(t)为均值为零、方差为σ2的白噪声样本函数,则称
[xt=0tntdt (5)]
为从原点出发的布朗运动或维纳过程。
白噪声是一种理想化的数学模型,由于其自相关函数是一个“冲击函数”,功率谱密度为“常数”,因此在数学上具有处理简单、计算方便等优点,在随机信号分析中占有相当重要的地位。
根据式(5)的单个布朗粒子位移数学模型,可演绎推导出单个布朗粒子在时域及频域的所有性质和运动规律,以及大量布朗粒子在t时刻服从(0,σ2t)正态分布的结论,与爱因斯坦布朗运动理论完全一致[6]。
七、结论
由于随机变量定义及概念的抽象性和复杂性,随机过程理论中出现了将单个质点位移假设为随机变量的基本概念错误。这一基本概念错误不仅导致研究对象从单个质点改变为质点集合,而且导致只能使用描述大量质点空间位置分布的统计规律来刻画单个质点的位移性质,从而得出了一系列与经验事实不符的错误结论,为自然科学、工程技术和社会科学提供了错误的理论、方法及工具。“与实际结合,问题驱动”是随机过程等应用数学学科发展的不竭动力和重要特征,因此,随机过程理论中关于质点随机运动的基本概念及研究方法将面临重大范式变革,新的質点随机运动理论将替代现有教科书中的内容,把人类对质点随机运动的认识提高到一个崭新的水平,为中国的随机过程学科进入世界一流学科前列提供了千载难逢的历史性发展机遇。
[ 参 考 文 献 ]
[1] 卡林,泰勒.随机过程初级教程[M]. 庄兴无,陈宗洵,陈庆华,译.北京:人民邮电出版社,2007.
[2] 王梓坤.布朗运动的若干结果[J]. 数学通报,1993(6):35-38.
[3] 钱敏平,龚光鲁,陈大岳,等. 应用随机过程[M].北京:高等教育出版社,2011.
[4] 樊平毅. 随机过程理论与应用[M]. 北京:清华大学出版社,2005.
[5] LI T C, KHEIFETS S, MEDELLIN D, et al. Measurement of the instantaneous velocity of a brownian particle[J]. Science, 2010,328(5986):1673-1675.
[6] 高宏. 公理化方法重建布朗运动理论[J]. 数学学习与研究,2020(23):133-134.
[责任编辑:林志恒]
