抽象思想在小学数学教学中的渗透

范睿

【摘  要】数学是一门逻辑性较强的课程，对学习者的思维能力有一定的要求，许多学生在数学学习中无法理解其中的逻辑关系，难以掌握抽象的数学概念与定理等知识点，加之教师采取的教学方法过于单一，从而影响了学生的数学思维能力发展以及学习兴趣的提升。抽象思想在小学数学教学中的渗透，符合数学学科的特点，能够带领学生从直观思维过渡到抽象思维的发展阶段，以促进小学生数学思想方法的掌握。

【关键词】小学数学；抽象思想；渗透

何为“抽象”？抽象是指舍弃事物的个别的、非本质的属性，抽取出本质属性的过程和方法，数学抽象思想是一种特殊的抽象思想，是只从事物的量的属性进行抽取的抽象思维，具有其本身的特点，具体体现在特定性、逻辑建构性、高度性三个方面。抽象思想是数学三大基本思想中最核心的思想，经历了数学的发展，在抽象思想下又演变出许多数学思想，如数形结合思想、分类思想及符号化思想等，由此可见，在基础教育阶段培养小学生形成数学抽象思想是十分有必要的，教师应加强对抽象思想渗透的重视程度，将抽象思想渗透于小学数学教学的全过程。

一、由“具体”引申到“抽象”

从儿童认识思维发展的规律角度出发，可以发现小学生的思维处于以具体形象思维为主的发展阶段，在小学数学教学中渗透抽象思想，需要以小学生的认知发展规律为前提条件，努力地创造出具体化、直观化、形象化的数学教学情境，带領小学生实现“具体”思想到“抽象”思想的过渡。为此，小学数学教师应将抽象思想渗透到每一个教学环节中，以具体、直观、形象的学习为基础，促使小学生初步建立抽象思维意识，助力小学生数学抽象思维的有序发展。以“梯形的面积计算公式推导”为例，教师可以借助具体的梯形图形操作引导学生推导出相关面积计算公式的由来，实现从“具体”到“抽象”的数学思想渗透，具体操作可以分为以下几点。

（一）组织猜一猜游戏活动，在图形观察中感知梯形面积的由来

在课堂导入环节，教师可以利用猜谜的游戏吸引学生的注意力，让学生通过对梯形纸片的细心观察、猜测、假设，将学习的注意力转移到梯形面积的学习中。例如，教师拿出一张梯形纸片，说道：“请同学们观察老师手中的梯形纸片，猜一猜这样梯形纸片的面积可能是多少？猜测数据越接近正确数值的学生获得胜利”，此时学生猜测的数值不同，学生也会对他人猜测到的数值产生质疑，有的学生猜测是12cm2，有的学生猜测是18cm2，也有的学生猜测是22cm2，教师应鼓励学生质疑，并结合自己观察到的图形阐述自己猜测数值的根据，说一说你为什么认为他人猜测的数值是不准确的。在这个过程中，学生对梯形纸片的观察，就是在具体思维作用下的直观感知，是建立在学生对具体事物观察下对梯形的边长、高度猜测基础上的理性思考，此时的梯形面积猜测是从直观感知中抽象思考得到的，带领学生进入抽象的数学世界，对小学生的数学抽象思想发展有一定的促进作用。

（二）引导学生在猜测之后探究，激活学生已有的数学学习经验

在抽象思维渗透的数学教学中，教师应善于运用学生猜想后的争议，引发新一轮的探究性学习活动，让学生在验证猜想的驱动下，开始调动脑海中积累的数学经验、生活经验，主动参与数学规律的探索。如在“梯形的面积计算公式推导”的这一知识点教学中，教师可以提出这样的问题：“我们已经就这个梯形的面积究竟是多少争论了一会儿了，那么想要知道梯形面积的具体数值有没有什么更科学的办法呢？”通过问题的提出引发了学生的理性思考与探究，学生开始从争论中走出来，希望可以用自己所学的知识科学地解决问题，证实结果，探索规律。有些学生想到可以将整个梯形纸片放在方格中，通过数方格的方式计算出面积，但是学生计算出的面积依然不同，有的计算出的结果是13cm2，也有不少学生计算出的是12cm2。为了进一步验证结果，教师可以组织小组合作的学习活动，要求小组成员合作完成梯形面积计算公式的探索任务，尝试运用不同的方式计算出正确的结果，可以动手操作，用剪刀将梯形纸片剪成若干个小块，并将其拼成一个规则的长方形，利用长方形面积的计算公式计算得出梯形的面积，还可以将梯形剪成几个三角形，利用三角形面积的计算公式计算出每一个三角形的面积是多少，再相加得出梯形的面积。或者将两个完全一样的梯形拼接成平行四边形，通过对梯形与拼接成的平行四边形的观察，可以发现拼接成的平行四边形的底就是梯形的“上底”和“下底”之和，高依旧是梯形的高，从平行四边形的面积计算公式可以抽象出梯形的面积公式是（上底+下底）×高÷2，带领学生在具体的、翔实的学习活动中，渗透抽象思想，帮助学生从具体思维过渡到抽象数学思维，掌握抽象归纳的数学学习方法。

二、由“简单”延伸到“抽象”

从“简单”到“复杂”，直至“抽象”是数学抽象思想发展的嬗变过程，为此教师在抽象思想的渗透中应尊重学习者的基本特征，如小学生理解能力相对较低、接受能力有限等，能够在抽象思想的渗透中创设出引发学生分析与思考的情境，引领学生从“简单”到“抽象”的思想形成过程中，获得理解能力与接受能力的稳步提升，使小学生在潜移默化中获得数学抽象思想发展。以三年级“观察物体”一课的教学为例，遵循由“简单”到“抽象”的思维发展规律，开展数学教学活动，具体如下：

（一）引导学生在观察与对比中，掌握数学图形的本质，抽象出立体图形的表象

在三年级的“观察物体”一课教学中，要求学生能够通过对最简单的正方体观察，发现正方体的基本特点，掌握观察立体图形的基本方法与规则，从对一个立体图形的观察过渡到多个立体图形组合而成的图形观察，进而抽象出立体图形的本质属性，带领学生从简单图形观察到抽象的立体图形特点与规则的探索中，能够让小学生的立体图形观察学习变得更具备灵性，也更理性。因此，教师应有方向地指导学生观察立体图形，如先让学生对手中大小不一的正方体立体图形精心观察，并比较分析几个正方形有什么相同之处，引领学生在简单的立体图形观察中发现正方体的基本特征是相同的，无论这个正方体是大还是小，都有6个面，且每一个面都是正方形，带领学生在最简单的正方形观察中建立简单立体图形的表象。

（二）将立体图形组合拼凑，引领学生在不同角度的观察中形成抽象思想

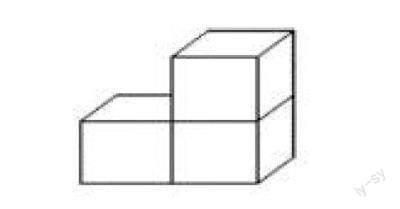
虽然对单个正方体的观察与对比可以促进小学生的抽象思想形成，但是其作用始终是有限的，除了对单个立体图形的观察，教师可以适当地增加难度，如给学生两个完全一样的正方体，让学生随意进行组合拼凑，再说一说两个立体图形的组合本质是什么。学生在实践操作之后，发现两个立体图形的组合方式虽然很多，但是其本上都是一个前一个后、一个上一个下，让学生尝试在组合之后画出正方体的组合图，实现从简单立体图形组合到抽象正方体组合图绘制的发展。在对实际的组合立体图形观察之后，教师还可以给学生出示一个立体图形的图片，如下图所示，要求学生按照图片中展示的样子摆一摆，摆好之后同桌之间相互检查是否正确，若是摆放的位置或方向不对，应及时纠正。教师与学生进行谈话，引导学生从“简单”过渡到“复杂”的数学思维中，如教师说道：“现在，我们先从正面观察这个物体，并剪出你所看到的形状，在桌子上将剪好的纸片摆出来，再从左面、右面、上面观察物体，用同样的方法将剪好的纸片摆放在桌子上，同桌之间交流，说一说：“从不同的方向观察三个正方体组成的立体图形，为什么会不同？你摸一摸最上面的正方体和其他两个是在同一个平面上吗，这和你看到的有何不同？”，由此引领学生在对简单的立体图形观察、组合后的立体图形观察以及平面立体图形的剪裁、对比分析中，进一步抽象出立体图形与平面图形的异同点，建立图形与几何领域的抽象思想。

三、由“感知”扩展到“抽象”

在小学数学教学中，教师可以从引领学生感悟新知的形成过程入手，促使学生在对数学现象的合情合理的抽象判断中，建构新知，完善认知。以“平行线的认识”一课为例，教师就可以遵循由“感知”扩展到“抽象”的教學方法，指导学生经历辨认同一个平面中两条直线相交的情形，在感知平行线的基础上，抽象出平行线的判断方法，具体方法如下：

（一）在绘制平行线中获得感知，在分类梳理中抽象平行线概念

首先，教师在黑板上画出3～4组平行线，让学生先观察每组中的两条直线之间的关系，在观察之后尝试画出两条相同构造的直线，让学生在观察以及平行线的绘制中初步感知什么是平行线。接下来，教师在黑板上画出几组不是平行线的直线，用反面例子引导学生意识到教师画的是直线，而根据已经学习到的知识认识到直线是无限延长的，在无限延长的直线绘制中，发现原本看似并不相交的直线在经过无限延长之后出现了交点，引领学生思考在什么条件下两条直线是平行的，进而提炼出“平行线”与“非平行线”的数学概念，引领学生在思考与感悟中，抽象出平行线的概念，为学生的数学抽象思想形成提供扎实的知识基础与思维保障。

（二）利用生活资源，引领学生在课堂之外积累数学抽象思想

数学抽象思想的渗透并不仅在书本中，教师还应将抽象思想的培养拓展到课堂之外，认识到脱离了生活的数学抽象思想渗透，会让数学教学失去原有的意义。因此，教师应将数学知识教学带出课堂，让数学抽象思想的感知与形成与生活之间无缝链接，带领学生在生活物体以及生活现象的观察中，获取更多的数学感知，形成更扎实的、有意义的数学抽象思想。如在“平行线的认识”一课课堂教学中，教师可以让学生在家庭中观察饭桌的两边、窗户的对边、火车的轨道，并根据所学的平行线知识判断这些生活中的物体是否是平行线，带领学生在生活中感知平行线、触摸平行线，也能从生活中发现许多不是平行线的直线，引领学生在对生活中的数学感知中，抽象出数学概念，建立数学抽象思维与生活的关系，促使学生将数学抽象思想运用于现实问题的解答中，达到学以致用的效果。

四、结束语

总之，抽象思想是数学教学中常见的思想方式，也是学生必须掌握的一种数学思想方法，在小学数学教学中渗透抽象思想，有助于小学生在大脑中针对所习得的数学知识建立更健全的认知，学会将直观看到的、简单表象的、切实感知到的数学进一步地分析，抽象出其中蕴含的数学规律，掌握数学现象的本质，对提升小学生的数学学习能力以及思维能力有重要的影响。因此，小学数学教师应积极探索抽象思想渗透的有效途径，掌握抽象思想培养的方法与策略，促使小学生在数学学习中形成抽象思维，促进数学思维品质的形成。

【参考文献】

[1]林宪.小学数学抽象思想渗透的思考和实践[J].试题与研究，2020（2）：154.