面向网络数据的Elastic Net回归模型

苏美红

（太原科技大学 计算机科学与技术学院，山西 太原 030006）

0 引言

线性模型作为一种经典的机器学习算法，不仅具有较为简洁的表示形式，而且具有较好的可解释性。传统的线性模型，通常是基于独立同分布假设的，忽略了数据之间的关联性，从而不能有效地适用于网络数据问题。然而，当前大数据时代，事物及其关联前所未有地以数据的形式被记录和收集，因而产生了大量的网络数据［1］。如何合理地将网络数据中包含的关联信息融入到回归模型中，以进一步提高线性模型的泛化性能，是机器学习领域一个重要的研究课题。

网络数据已广泛存在生活中的方方面面，如生物制药、智能交通、电子商务、疫情防控等［2］。网络数据作为一种数据表现形式，能够有效地刻画和描述数据之间的关联性。基于此，面向网络数据的回归模型引起了学者们的广泛关注。目前已有的基于网络数据的回归模型均是基于属性之间的关联性，忽略了输出变量（或标签）之间的潜在结构信息，进而影响了回归模型预测的准确度。近期，Network Lasso［3］通过构建含有输出变量之间的网络结构图，并利用平方损失和L1正则化对参数进行选择和估计，为解决上述问题提供了一种新思路。然而，当变量之间相关性较强时，该方法的性能会明显减弱；而且面向高维小样本数据，容易导致模型过度稀疏化。为解决上述问题，基于含有输出变量结构信息的回归模型，本文提出了面向网络数据的Elastic Net 回归模型。该模型主要包含有平方损失函数项和Elastic Net 正则项两部分，第一部分平方损失函数项既包含有样本属性信息，又包含有样本输出变量之间的结构信息；第二部分Elastic Net正则项由L1和L2组成，前者具有变量选择能力，后者可以处理共线性问题，并且具有一定的稳定性。综上，所提模型有效地解决数据共线性以及模型过度稀疏问题，从而进一步提高了回归模型预测的准确性和可解释性。其主要贡献如下：

（1）构建了一种含有样本结构信息的回归模型，避免了传统线性模型独立同分布的基础假设。

（2）提出了一种面向网络数据的回归模型算法，既包含网络数据的结构信息，又能够有效处理强相关性问题，避免了模型过度稀疏化。

1 面向网络数据的回归模型

网络数据［4］通常用图来表示，图中每个节点代表一个具体的网络实体，如社交网络中的一个用户；节点之间的连接边代表实体之间的关系，如两个用户之间的好友关系。近十年来，随着数据采集技术的蓬勃发展，数据不仅呈现出了上述网络结构的特点，而且具有高维性。因此，如何有效地分析或处理高维网络数据成为了机器学习、计算机科学、生物信息等领域的研究热点［5-7］。目前关于网络数据的研究主要集中在两个方面，一方面是关于网络结构的研究［8-9］，另一方面主要考虑将网络数据中的结构信息与机器学习中常用的经典模型相结合［10-11］。前者旨在根据数据估计未知的网络结构，典型的方法有罚似然估计和邻居选择方法［12］。后者主要是利用机器学习模型对网络数据进行分析，以便作进一步推断或预测。本文将重点关注于后者，具体地，本文将聚焦于回归模型与网络结构信息相结合的研究。

高维性已经成为了网络数据的基本特点之一，高维问题的本质特点是具有稀疏性，即数据表面上维数很高，但本质上具有低维结构［12］。以高维线性模型为例，虽然输入变量的维数或属性个数远大于样本数，但事实上，对输出变量有重要影响的属性很少。正则化方法的提出，为求解高维问题提供了一种有效的途径。在此基础上，以Lasso 为代表的一类回归模型具有了变量（特征）选择能力，如自适应Lasso［13］、LAD-Lasso［14］、SCAD［15］等。基于回归模型的网络数据分析也引起了相关学者的注意。例如，Zhu 和Levina 等［16］提出了一种网络链接数据的预测模型，他们在个体模式效应中引入了基于网络的惩罚，以表示链接节点的预测因子之间的相似性，该方法是点估计问题的回归版本［17-18］。此外，在贝叶斯框架下，该方法可解释为应用高斯马尔可夫随机场作为先验的网络回归问题。在经济学中，Manski［19］对社交网络展开研究；Asur 等［20］通过研究网络结构来对现实生活场景进行预测。上述工作利用回归模型对网络数据进行了有效的分析，由此也表明网络数据在回归模型中重要的研究价值。然而，考虑样本输出变量的网络结构信息尚未得到充分的研究。尤其在回归模型构建中，并未合理利用输出变量之间的网络结构信息。近期，Su 等［3］通过网络图将样本之间存在的潜在结构信息引入的回归模型中，提出了Network Lasso 模型，通过网络图将样本邻近信息加入回归模型中，提高了模型的预测精度；另一方面，在估计回归模型参数时，通过L1正则项达到了变量选择的能力。然而，上述方法存在明显不足，一方面缺乏稳定性，容易导致较大波动；另一方面忽略了变量之间的共线性问题，从而使得回归参数估计的准确度降低，进而影响了回归模型的预测精度。

针对上述问题，本文提出了一种新的基于L1和L2正则项的Network Elastic Net 回归模型，前者L1正则项能够保证模型的稀疏性；后者L2正则项既可以保证模型的稳定性，又能够有效解决变量之间的共线性问题。

2 Network Elastic Net回归模型

线性回归模型形式简单、易于建模，同时蕴含着机器学习中一些重要的基本思想，很多功能更为强大的非线性模型可在线性模型的基础上通过引入层次结构或高维映射而得到［21］。此外，由于线性模型中的回归参数直观地表达了各个输入变量或属性特征在预测中的重要性，从而使得线性模型具体很好地可解释性。

2.1 线性回归模型

线性模型通常具有如下形式：

其中Y=(y1，y2，…，yn)∈Rn为n维响应向量，yi(i=1，2，…，n)表示第i个样本的输出值，n为样本个数；X=(X1T，…，XjT，…，XpT)∈Rn×p为设计矩阵，p为输入变量个数，Xj=(x1j，x2j，…，xnj) 表示第j个输入特征；β=(β1，…，βp)T∈Rp为回归模型参数；ε=(ε1，ε2，…，εn)T为模型误差向量。当参数β确定后，模型得以确定。因此，根据给定数据集估计回归参数是线性模型的根本目标。

经典的回归模型参数估计方法为最小二乘估计（Least Squares estimator，LS）［22］，即

正则化方法［23］始于20 世纪40 年代积分方程的研究。近年来，正则化已成为稀疏建模和变量选择的有效方法，其基本思想为在目标函数上加入关于模型参数的惩罚函数项或正则化项来降低模型的复杂度，其中基于最小二乘的正则化模型应用最为广泛，如Lasso［24］。Lasso（Least Absolute Shrinkage and Selection Operator）是Tibshirani 提出的基于平方损失的正则化方法，能够同时实现变量选择和模型参数估计。其模型如下：

其中λ≥0 为正则化参数，为参数向量β的L1范数。

Lasso 回归使用L1范数作为惩罚函数项，通过对参数β施加一定的约束，使得部分参数取值为0，从而实现了变量选择的能力。在此基础上，各种不同的惩罚函数被提出，从而产生了多种不同的正则化回归方法，如L1/2［25］，Adaptive Lasso［26］，Elastic Net 回归［27］，SCAD（Smoothly Clipped Absolute Deviation）［28］，MCP（Minimax Concave Penalty）［29］，Hard 阈值罚［30］等等。上述正则化回归模型均具有变量选择的能力，因而被广泛应用于矩阵分解［31］，多标签学习［32］，多目标学习［33］等。此外，上述方法还可用来处理不平衡数据。进一步，面向网络数据的正则化方法也引起了相关学者的关注［34］。

2.2 Network Elastic Net模型构建

为提高模型预测的准确性，在拟合过程中，不仅考虑每个样本的预测变量xi对其响应变量yi的影响，同时考虑其邻接样本yj(j=1，2，…，n) 对其产生的影响，具体构建模型如下：

其中i=1，2，…，n，yi代表第i个响应变量，xi代表第i个预测变量，εi为模型误差，β∈Rp为对应的p维待估回归参数，yj(j∈Mi)表示与yi具有连接关系的响应变量，αj为相应的影响系数，Mi表示与yi相连接的响应变量组成的集合，即Mi={j|(yi，yj)∈E)}。

为便于理解与计算，本文假设第i(i=1，…，n)个响应变量yi的所有连接变量yj对其有相同的影响，并令其为α，即αj=αj'=α(j，j'∈Mi)。从而，构建模型如下：

进一步，为估计未知回归参数β，本文考虑如下正则化估计：

其中第一项为损失函数项，度量学习结果在数据上的误差损失；第二项为L1正则项，能够保证模型的稀疏性；第三项为L2正则项，具有强凸性，因而参考文献［27］中引理2，可知当数据中的因变量xi1和xi2具有相关性时，该模型有能力将xi1和xi2同时选出或剔除，即具有组变量选择的能力；λ1和λ2为大于0 的正则化参数，λ1越大，模型的稀疏性越强。

将回归模型（1）重新整理成矩阵形式如下：

其中矩阵A∈Rn×n为图G的邻接矩阵，如果(u，v)∈E，则Auv=1，否 则Auv=0；ε=(ε1，ε2，…，εn)T为n维模型误差向量，εi服从高斯分布。相应地，模型（2）重新整理如下：

由Zou 等［27］可知，L1+L2范数称为Elastic Net 正则项（或罚函数），故将式（3）称为面向网络数据的Elastic Net 回归模型，即Network Elastic Net 模型。特别地，当λ2=0 时，上述模型即为Network Lasso。与Network Lasso 相比，文所提模型增加了L2正则项，L2正则项是各个元素的平方之和，具体强凸性，因而本文所提模型具有组变量选择的能力。

其中γ∈(0，1)，当γ=1 时，上述模型即为Network Lasso。显然，对于模型（3），参数λ1∈(0，∞)，λ2∈(0，∞)；而在上式中λ1∈(0，∞)且γ∈(0，1)。因此通过引入参数γ可降低模型参数选择的难度，提高计算效率。

2.3 Network Elastic Net模型求解

本小节详细介绍所提模型（3）的求解算法，本文分别考虑影响系数α已知和未知两种情况。为便于理解，对（3）式进行推导。

（1） 当α已知时，本文采用坐标下降法求解回归参数β，具体如下：

对上式右边求导，并令所求导数为0，可得

其中若βj＞0，则e=1；若βj＜0，则e=-1。

对上式进一步整理，可得

即

其中Shrink[u，η]=sgn(u)max(|u|-η，0)。

进一步，可得

（2）当α未知时，本文采用交替迭代和坐标下降法进行求解。

首先，固定β，求解α如下：

根据坐标下降法，可求得

其次，固定α，求解β，所得结果同（4）。

因此，当α未知时，交替迭代公式（4）和（5）可分别求得参数α和β，直到收敛。

综上，求解Network Elastic Net 的算法步骤如算法1。

算法1 Network Elastic Net 模型求解算法输入：数据D={(xi，yi })n i=1，参数γ ∈(0，1)，正则化参数λ，迭代误差δ，邻接矩阵A。输出：回归参数β 和影响系数α。Step 1.初始化：给定初始值β0。Step 2.Repeat根据公式（1.5）更新α。根据公式（1.4）更新β。Until■■β̂k-β̂k-12 ≤δ。

3 Network Elastic Net回归模型

本节通过人工数据集上的实验来验证所提模型Network Elastic Net 的有效性，并与Network Lasso 和Lasso 进行比较。此外，为了尽可能准确全面地利用样本之间的网络结构信息，本节考虑三种最常用的网络结构图，分别为Scale-Free（SF）网络，Hub 网络和Erdös-Renyi（ER）网络。具体结构形式如图1。

图1 样本量n=100的三种网Fig.1 Three kinds of network graph with n=100

3.1 数据集及评价指标

本文参考文献［3］生成实验数据，具体假定样本量个数n=100；预测变量维数p=50，100，200，300，400；设计矩阵X中的每一行服从正态分布N(0，Σ)，Σ=(σij)，σij=0.5||i-j；模型误差εi服从标准正态分布N(0，1)，真实回归系。在此基础上，响应变量Y按

生成，并固定α=2；A为上述网络结构图的邻接矩阵。

此外，定义几个评价指标如下：

（1）Lq损失：；

（3） 变量选择个数N：N=#{j：j≠0}；

（4）F1-score：2TP/(2TP+FP+FN)。其中TP=#{j：β0j=0，且j=0}；FP=#{j：β0j=0，且j≠0}；FN=#{j：β0j≠0，且j=0}。

针对每一种网络图，首先比较了不同γ值对所提方法的影响，分别考虑了γ=0.2，0.35，0.5，0.65，0.8 等5 个不同的值。其次研究了不同维度下本文所提方法的预测与变量选择能力。最后将本文所提模型Network Elastic Net（E-Netlasso）与Network Lasso（Netlasso）、Lasso 进行了比较，以此验证所提方法的有效性。下面分别以三种网络图为例进行具体的分析和讨论。

3.2 SF网络

3.2.1 参数γ对模型的影响

本小节研究γ值对E-Network 模型的影响，具体包括模型预测准确度和变量选择能力两方面，实验结果如图2 所示。

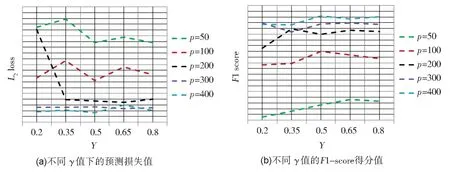
图2 SF网络中γ对模型的影响Fig.2 Influence of γ in SF network on the model

图2（a）给出了本文所提方法在不同维度下取得的L2损失值随参数γ的变化情况，进而衡量本文所提方法在不同γ值下的预测效果。由图可知，当样本维度p=50 或100 时，L2损失值在0.5 处取得最小值，即E-Network 的预测准确度最高；当p=200 时，随着γ的增大，L2损失值减小并趋于稳定；当p=300 时，L2损失值基本取得了相同的值；当p=400 时，L2损失值在γ=0.2 和0.5 之间基本相同，随着γ的增大，L2损失值先增大后减小。整体而言，当维数较高（大于样本个数）时，本文所提方法E-Network在不同的γ值下所得误差基本相同，由此表明参数γ对E-Network 影响较为稳定。当维数较低时，E-Network 在0.5 处取得最小损失值，此时预测精度最高。

图2（b） 展示了本文所提方法在不同γ值下的变量选择结果。由该图可知，当样本维度p=50 时，随着γ的增大，F1 分数值逐渐增大，在γ=0.65 处达到最大；当p=100 时，F1 分数值在γ=0.5 处达到最大；当p=200 时，随着γ的增大，F1 分数值先增大后减小，在γ=0.35和0.65 处达到最大，在γ=0.2 处最小；当p=300 或400 时，F1 分数值均在γ=0.5 处取得最大。综上可得，参数值γ对本文所提方法在变项选择方面较为敏感。综上可得，当γ=0.5时，E-Network 在预测准确度和变量选择方面均取得了较好的结果。更为全面详细的实验结果请参见附录2 表1。

3.2.2 不同p值下的实验结果

本小节研究了本文所提方法随样本维度p的变化情况。为使得结果更加清晰明了，固定γ=0.5，结果如图3 所示。

图3（a） 给出了L2损失值随p的变化情况，从图中可以看出随着维数的增大，L2损失值越来越小，即本文所提方法的预测准确度越来越高。由此说明E-Network 在高维情况下表现效果更好。图3（b）和3（c）分别从变量选择个数N 和F1分数值两方面展示了E-Network 在变量选择方面的能力。由图（b）可知，当p=100 或400 时，所选变量比较少；当p=200 或300 时，所选变量几乎相等；当p=50 时，介于上述两者之间。由图（c）可知，随着维数的增高，变量选择的准确度越来越高。由此可得，当p=100 时，E-Network 选择了较少的变量且准确度较低；当p=50 时有类似的结果；当p=200 或300 时，模型所选变量个数较多，但准确度较低；当p=400 时，E-Network 所选变量个数最少且准确度最高，即所选的非零变量与真实的非零变量比较一致。综上可得，当样本维数较高时，E-Network 在模型预测精度和变量选择方面均取得了较好的结果。

3.2.3 三种方法的比较结果

本小节将所提方法E-Network 与Lasso 及Netlasso 进行比较，具体结果与分析如下。

图4 给出了三种方法在不同维度下的损失值和变量选择结果。由图4（a）可得，随着维数的增加，Lasso 和Netlasso 的L2损失值先减小后增大，后又减小；而E-Netlasso 的L2损失值持续减小，且远小于Lasso 和Netlasso。图4（b）和4（c）显示，在p=50，200，300 的情况下，本文所提方法的变量选择效果优于其他两种方法；在p=100 时，Netlasso 表现最好，E-Netlasso 次之；在p=400 时，Lasso 表现最好，E-Netlasso 表现最差，其原因在于参数γ和λ的选择较大，从而使得其稀疏性更强。

综上可知，无论是低维数据，还是高维数据，本文所提方法均取得了最小的损失值，从而说明本文所提方法E-Network 具有更为准确的预测效果。在特征选择和模型选择方法，本文所提方法均可以取得最优或与次优的结果。整体而言，相比于Lasso 和NetLasso，E-Network在预测和变量选择方面均有较好的效果，尤其对于高维数据。由此说明，该方法能够更好地处理变量的共线性问题，进而进一步提高模型预测的准确度。

3.3 Hub网络

3.3.1 参数γ对模型的影响

下图展示了L2损失值和F1 分数值随参数γ的变化情况。

由图5（a）可得，当p=50 或100 时，E-Network 的L2损失值随γ的变化波动比较大，其中p=50 时在0.35 处取得最小值，0.65 处次之，0.2处为最大；p=100 时在0.65 处，L2损失值最大，在0.35 和0.5 处几乎相等且最小。当p大于等于200 时，随着γ的增大，L2损失值基本趋于稳定，尤其当p=300 或400。图5（b）给出了ENetwork 模型不同维度下F1 分数值随γ的变化情况。当p=50 和100 时，随着γ值的增大，F1分数值的变化趋势基本一致，且均在0.2 处和0.65 处取的了几乎相等的最小值。当p=200时，在0.5 处变量选择效果最好，在0.35 和0.65处最差。当p=300 或400 时，随着γ的变化，F1分数值几乎保持不变且取值较大。综上可得，本文所提模型在预测和变量选择方面，当样本维数较低时，受γ影响较大；当维数较高时，对参数γ敏感度较小。更为全面详细的实验结果请参见附录2 表2。

3.3.2 维度p对模型的影响

本小节研究了样本维度p对模型的影响。类似地，固定γ=0.5。

图6（a）展示了所提模型在不同维度下的预测效果，图6（b）和6（c）分别给出了所提模型在不同维度下的变量选择个数和F1 分数值，用来衡量E-Network 模型的变量选择能力。由图（a）可知，随着维数的增高，E-Network 的损失值呈下降趋势，在p=300 处取得最小，随后略有增高，但均远小于p=50 时所得损失值。由图（b）可知，当p=400 时，所选变量个数最接近于真实值，且由图（c）可知F1 分数值也较大，即模型可以以很大的概率选出与真实模型一致的非零变量。类似地，从图（b）可知当p=50 到300 时，模型所选变量个数远远小于真实的值。同时由图（c）可知，F1 分数值随着维度的增高而增大，即当p=300 时，虽然模型所选变量个数较少，但精度较高；相反地，当p=50 时，模型所选变量个数较少且精度很低。

3.3.3 三种方法的比较结果

将本文所提方法E-Network 与Lasso、Netlasso 进行了比较，具体结果与分析如下。

图7（a）给出了三种模型的L2损失值，用来衡量各个模型预测的准确度。由图（a）可知，本文所提模型的L2损失值远小于其余两种模型，尤其当p=300 时。且整体而言，随着维度的变化，E-Netlasso 模型的L2损失值波动较小，相对比较稳定，其次是Netlasso，Lasso 表现最差。图7（b）和7（c）分别展示了三种模型的变量选择个数和F1 分数值，用来衡量模型的变量选择能力。由（b）可知，除p=300 外，E-Netlasso 取得的变量个数均最接近于真实值。由图（c）可知，E-Netlasso 所得F1 分数值随维数的增高而增大，且均大于其余两种模型所得值。当p=300 时，Netlasso 所选变量个数最接近于真实值，但由图（c）可知其准确度较小。综合（b）和（c）可得，E-Netlasso 在变量选择方面可取得最优或次优。综上可得，E-Netlasso 在回归模型预测和变量选择方法均优于Netlasso 和Lasso。

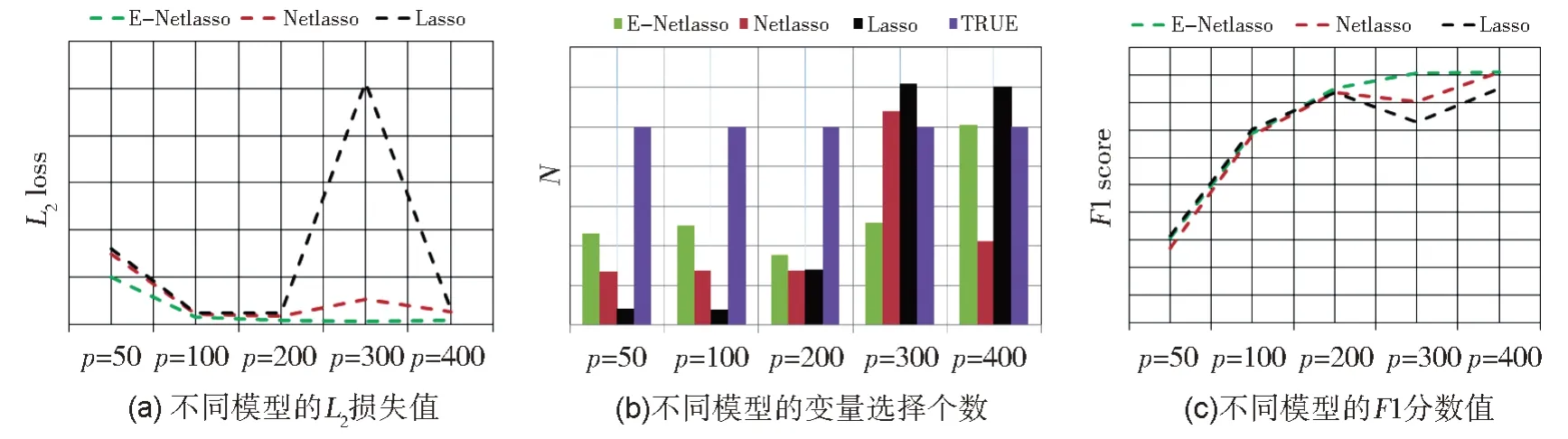
图7 ER网络中γ对模型的影响Fig.7 Influence of γ in ER network on the model

3.4 ER网络

3.4.1 参数γ对模型的影响

图8 展示了L2损失值和F1 分数值随参数γ的变化情况。

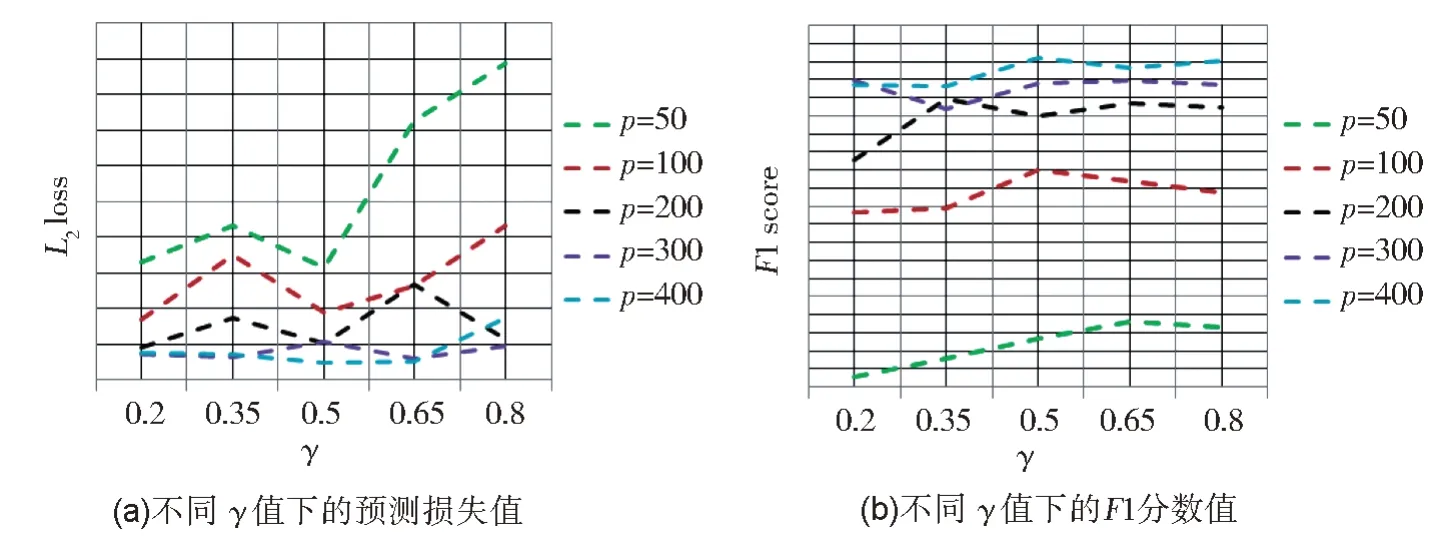
图8 SF网络中γ对模型的影响Fig.8 Influence of γ in ER network on the model

类似于Scale-free 网络和Hub 网络，当维度较低时，E-Netlasso 对参数γ较为敏感，尤其在模型预测方面。当维度较高时，E-Netlasso 模型受参数γ影响相对较小。更为全面详细的实验结果请参见附录2 表3。

3.4.2 维度p对模型的影响

图9 给出了固定γ值，E-Network 随p变化的L2损失值、变量选择个数及F1 分数值。由图（a）可得，随着维度的增大，L2损失值逐渐减小，在p=400 处取得最小值。由图（b）和（c）可得，当p=300 时，所选变量个数大于真实值，但正确率略有偏小。当p=400 时，所选变量个数小于真实值，但正确率相对较高。当p=50 时，变量选择个数及正确率均最差。综上进一步可得，本文所提模型在高维情况下在模型预测和变量选择方法均较好。

图9 Hub网络中p对模型的影响Fig.9 Influence of p in ER network on the model

3.4.3 三种方法的比较结果

图10 展示了三种模型的L2损失值、变量选择个数及F1 分数值，用来比较三种模型的预测和变量选择能力。显然，在预测方面，由图（a）可知，E-Netlasso 要远远优于其他两种模型。结合变量选择个数和F1 分数值，E-Netlasso 同样可以达到最优或次优。综上，当邻接矩阵为ER网络图时，本文所提方法仍可取得最好的实验结果。

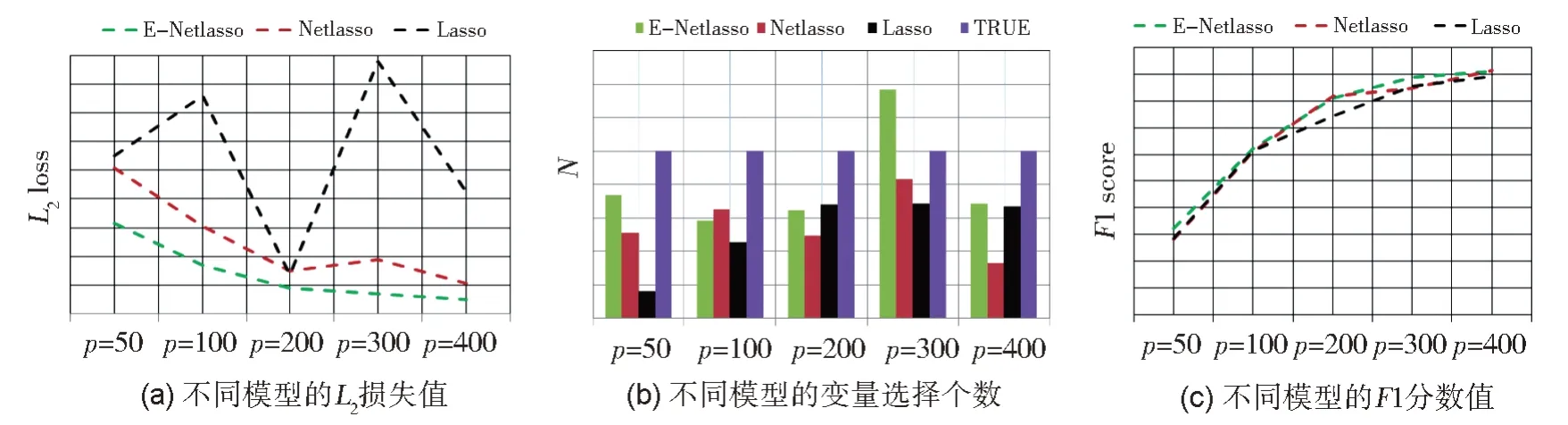
图10 Hub网络下三种模型的比较Fig.10 Comparison of three models under ER network

4 实际数据分析

本节将所提方法应用于房屋价格预测数据来验证其有效性。该数据来源于R 语言中的igraph 包，记录了2008 年5 月某地区一周内的房地产交易信息，共包含有985 个交易数据。每项交易中包括纬度、经度、卧室数量、浴室数量、房屋面积和销售价格等信息。

在实验中，将价格和所有属性均进行了标准化处理，使其均值为0，方差为1。实验中随机选用200 个数据作为测试集，剩余数据作为训练集。此外，本节根据每个房子的经度和纬度坐标来构建训练集和测试集上的网络图结构，对于任一样本i，其相邻个数g分别考虑3，5，7，10，所有的，即g=3，5，7，10，All 多种情况。对于影响系数α，本文选用与两房屋之间距离成反比的权重值连接。需注意的是，如果房屋j在房屋i的最近邻集合中，那么无论房屋i是否是房屋j的最近邻居之一，它们之间都存在一条无向边。进一步，本实验使用样本内平均平方预测误差 （In-sample mean squared prediction errors）和样本外的平均平方预测误差 （Out-sample mean squared prediction errors）来评模型的优劣。基于模拟实验结果，选取参数γ=0.5。

首先，比较了 Lasso，Netlasso 和E-Netlasso三种方法在各个g下的实验结果。在此，仅对g=3 的实验结果进行详细的分析讨论，其余几种情况将在附录中给出其实验结果。

图11 给出了样本连结个数为3 时的实验结果。由图11 可知，无论是在测试集上，还是在训练集上，本文所提方法都取得了最小的均方误差值，Netlasso 次之，Laaso 表现最差。由此可知，在构建回归模型时，加入样本的网络结构信息有利于提高回归模型预测的准确度。

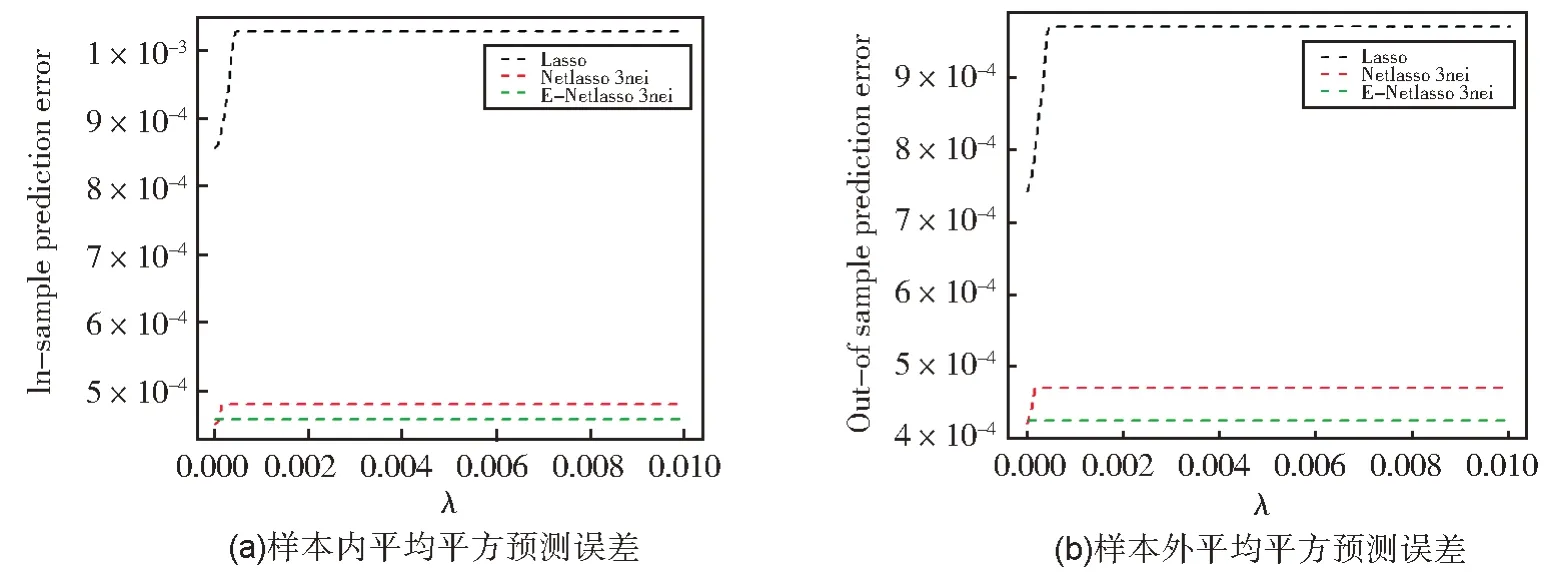
图11 g=3时三种模型的比较Fig.11 Comparison of three models under g=3

其次，分别比较了Netlasso 和E-Netlasso 两种方法在各个相邻个数下的实验结果。

图12 分别给出了Netlasso 在样本连接个数分别为3，5，7，10，All 五种情况下的测试集和训练集上的均方误差值。由此可以看出，当个数为10 时，Netlasso 表现最好；当个数为3 时，Netlasso 表现最差，当考虑所有样本时，其表现次之。当样本个数为5 和7 时，Netlasso 取得了几乎相近的均方误差值，尤其在训练集上。值得注意的是，在训练集上取得的误差值略小于测试集上，其原因或许在于样本量的大小对其产生的影响。

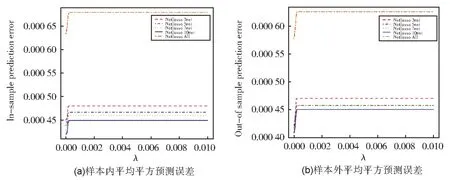
图12 不同g下Netlasso的实验结果比较Fig.12 Performance of Netlasso under different g

图13 分别给出了E-Netlasso 在不同样本连接个数下的测试集和训练集上的均方误差值。同样的，当g=10 时，本文所提方法表现最好；当g=3 时，表现最差。此外，由图（b）可知，当g=5，7，All 时，Network Elastic Net 具有相近的表现效果，且均大于在g=10 时取得的误差值。由此说明，当利用网络结构图构建回归模型时，其连接个数的数量对结果的影响尤为重要。因此，如何有效合理地选取合适的样本连接个数值是值得探讨的。

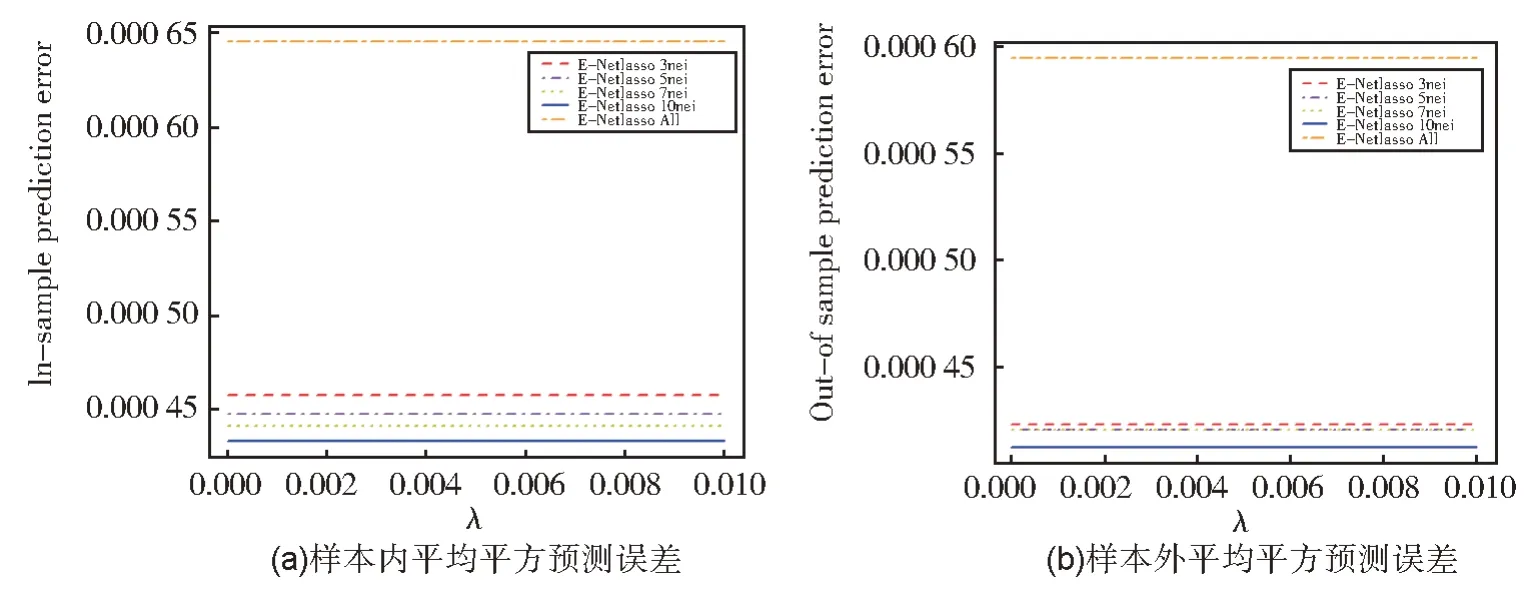
图13 不同g下E-Netlasso的实验结果比较Fig.13 Performances of E-Netlasso under different g

5 结语

为了有效处理网络数据中的变量相关性问题，本文提出了一种面向网络数据的Elastic Net回归模型。该模型既具有变量选择的能力，又能够有效处理变量的相关性问题。进一步，所得研究结果表明，本文所提方法无论是预测损失还是变量选择的准确性都有明显改善，尤其面向高维网络数据。

本文所提模型为具有强相关性变量的网络数据提供了一种新的解决思路。此外，在回归模型构建中加入样本邻接样本信息能够提高模型预测的准确度，然而，如何选恰当地选择邻接样本个数仍是值得探讨的重要问题之一。