二维1T'-MnSe2材料拓扑态的研究

薛林，崔慧芹，陈波

（太原理工大学 物理与光电工程学院，山西 太原 030024）

0 引言

量子反常霍尔 （QAH） 绝缘体又称Chern绝缘体，是一种以非零Chern 数和体能隙中手性边缘态为特征的新型拓扑相［1-3］。Chern 绝缘体具有内部磁交换相互作用 （铁磁或反铁磁）引起的时间反演对称 （TRS） 破缺、自旋轨道耦合 （SOC） 产生的能隙以及能隙中无间隙手性边缘态等特征。与二维量子自旋霍尔效应中观察到的自旋极化螺旋性边缘态不同［4-6］，Chern 绝缘体中的边缘态只允许一种自旋态单向流动，从而产生量子霍尔电导δxy=(e2/h)C（C为Chern 数）。这种边缘态不受缺陷、无序和表面污染等的干扰。因此，Chern 绝缘体在低功耗电子和自旋电子器件中具有广泛的应用前景［7］。理论上，在量子自旋霍尔绝缘体（QSHI） 中引入铁磁序从而打破时间反转对称性是实现量子反常霍尔效应 （QAHE） 的有效途径［8］。根据理论预测，QAHE 现象在极低温（30 mK 以下）下 Cr 掺杂的 （Bi，Sb）2Te3薄膜中被成功观察到［9］。由于二维材料的快速发展及其优异的性能，QAH 的研究扩展到各种二维单层材料［10-14］。在二维石墨烯［10］和硅烯［11］中进行过渡金属 （TM） 原子的化学掺杂，发现了QAH 相。但由于其结构的复杂性在实验中难以控制［15］。寻找简单电子结构、大带隙、高温、高载流子迁移率的QAH 材料对QAH 的实际应用具有重要意义。

随着自旋电子学中自旋无间隙半导体（SGSs） 概念的确立［16］，在简单的Kondo 晶格模型的基础上［17］，提出了Dirac 半金属 （DHM）相。DHM 是指在一个自旋通道打开带隙的同时，另一个自旋通道存在无带隙狄拉克锥的材料。无质量的狄拉克费米子表现出100%的自旋极化，且具有极高的载流子迁移率［18-19］。显然，如果在狄拉克点打开一个拓扑非平凡带隙，可以让DHM 转变为QAHE［20］。理论上，已经证实在考虑SOC 效应后，部分DHM 具有QAH 特性［20-25］。例如，在考虑SOC 效应后，Pd-Cl3费米能级附近的Pd-dxz和Pd-dyz产生能级劈裂，具有非零Chern 数 （C= -1） 和手性边缘态的特征，表现为QAHE［20］。NiCl3（单层DHM） 在考虑SOC 效应时，打开24 meV 的拓扑非平凡带隙，从而变成本征Chern 绝缘体［22］。CrMnI6单分子层具有13 meV 的拓扑非平凡带隙和更高的Chern 数 （C= 2），是本征QAHE材料［24］。目前理论上构建的二维DHM 型QAH 材料集中在六角结构，能否在其他结构如四角结构中构建DHM 并研究其QAHE 效应呢？

基于以上构思，通过第一性原理计算方法，借鉴二维1T'-WTe2结构，此工作构建了二维1T'-MnSe2结构并通过结合能、形成能和声子谱的计算证实结构的稳定性。在不考虑SOC 效应时，其铁磁态是一种新型的d 态DHM，自旋极化狄拉克点位于第一布里渊区的两个非对称不可约 D 和 D' 点。进一步考虑SOC 效应时，在狄拉克点自旋向下的通道中打开约40 meV 的带隙。非零Chern 数 （C= -1）、量子霍尔电导率和无间隙手性边缘态均证实了1T'-MnSe2是本征Chern 半金属，为DHM 型的QAH 材料，有机会应用在自旋电子学领域。

1 计算方法

本文采用基于密度泛函理论 （DFT） 的VASP （Vienna Ab-initio Simulation Package） 软件包计算［26-28］。通过投影缀加平面波方法（PAW） 描述原子核与电子相互作用，采用基于广义梯度近似的PBE 交换关联函数描述电子交换关联泛函［29-30］。在求解过程中以截断能为500 eV 的平面波基组进行展开。计算电子结构时，第一布里渊区采用Monkhorst-Pack 方法选取以Γ 为中心13×9×1 的网格。能量收敛标准为每个单胞能量小于1×10-5eV，对所有原子进行弛豫直到原子受力小于0.01 eV/Å。为了消除相邻层之间的相互作用，添加15 Å 的真空层。此外，通过PHONOPY 用线性响应理论计算结构声子谱［31］；用Wannier90［32］和WannierTools［33］计算单层结构的局域边缘态。对于过渡金属Mn 原子的3d 轨道采用Hubbard U 进行校正 （DFT+U 方法），在约束随机相位近似（cRPA）［34-35］的框架下获得Hubbard U 的值。

2 结果与讨论

1T'相单分子层过渡金属二卤族化合物（TMDCs） MX2［36-38］，M=（W，Mo）和X=（Te，Se，S）中的大能隙QSH 绝缘体性能而受到理论界和实验界的广泛关注。我们用具有3d 轨道的过渡金属Mn 替代1T'相TMDCs 中的金属原子以实现二维DHM。如图1（a）和（b）所示，二维1T'-MnSe2的晶体结构为1T'-WTe2型晶胞，其空间群为P2_1/m（No.11），具有典型的矩形晶格，单层Mn 原子被夹在四层Se 原子之间，每个单胞中含有四个Se 原子和两个Mn 原子，其中，Se 原子具有两个不等价位Se1 和Se2。优化得到二维1T'-MnSe2的晶格常数为a=3.302 Å，b= 5.631 Å。为了评估体系的稳定性，用以下公式分别计算其结合能Ec和形成能Ef：

图1 二维1T'-MnSe2的 （a） 俯视图和 （b） 侧视图 （紫球和黄球分别代表Mn和Se原子）；（c） 1T'-MnSe2的第一布里渊区和高对称点，红色点表示狄拉克点D和D'的位置；（d） 二维1T'-MnSe2声子谱Fig.1 (a) Top and (b) Side views of 2D 1T＇-MnSe2 monolayer (the purple and yellow balls represent Mn and Se atoms, respectively); (c) First Brillouin zone of the 1T＇-MnSe2 monolayer and high symmetry points, the positions of Dirac point D and D＇ are signed by red points.(d) Phonon spectra of 2D 1T＇-MnSe2

其中，EMnSe2表示1T'-MnSe2单胞的总能量，EMn-f和ESe-f分别表示单个Mn 原子和Se 原子的能量，EMn-s和ESe-s分别表示Mn 原子和Se 原子在自然单质中的能量，n和m表示单胞中Mn 和Se 的原子个数。计算得到Ec=3.521 eV/atom和Ef=-3.478 eV，1T'-MnSe2的结合能比1TMnSe2低0.05 eV［39］。结果表明，1T'-MnSe2结构中原子间键能较强，具有较高的稳定性。对1T'-MnSe2的声子谱进行计算，如图1（d）所示，没有虚频，证实1T'相具有动力学稳定性。

计算中考虑了不同的反铁磁态 （AFM） 和铁磁态（FM） 以确定1T'-MnSe2 的基态。从附件材料中图1S 所示的5 种反铁磁态和铁磁态及相应总能的计算结果可以得到最稳定的AFM 态比FM 态每个单胞能量低0.14 eV，两相直接存在强烈竞争。从能带图 （附件图2S） 看到，AFM 基态在忽略SOC 作用时形成无间隙的狄拉克锥，但是这时体系没有磁矩不利于反常霍尔效应的研究，本文主要研究其在FM 态下的拓扑性能。图2（a）所示为二维1T'-MnSe2加自旋极化的FM 态的能带图。可以看到，其自旋向上和自旋向下的能带完全不同。在自旋向下的通道中，在费米能级以下0.14 eV 处沿着Γ-X 的高对称路径形成一个无间隙的狄拉克点。在自旋向上的通道中，在高对称 Y 点附近的价带顶穿过费米能级呈现金属态，并在费米能级上方存在0.32 eV 的间接带隙。由于高度的自旋极化，二维1T'-MnSe2层具有1.97 μB 的较大磁矩。此外，如图1（c）和图2（a） 所示，自旋极化狄拉克点位于第一布里渊区的两个非对称不可约 D 和 D' 点，与传统的狄拉克半金属的位置不同，例如，石墨烯中的狄拉克点位于高对称的不可约K 和K' 点。这种狄拉克点的偏移是由两层硒原子中三角形晶格的不对称性引起的，在其他二维体系［21，40-42］（如1T-YN2）中也观察到类似的非对称的狄拉克点，会导致材料与物理性质各向异性相关的多面性［40］。费米速度［43］（vf） 作为狄拉克半金属的重要参数，通过用公式hvf=ΔE/Δk 拟合高对称 D 或D' 点周围的能带得到。二维1T'-MnSe2沿 Γ-X方向的费米速度为4.1×105m/s，沿 Γ-Y 方向的费米速度为1.54×105m/s，与硅 （5.3×105m/s）［44］的费米速度相当，可作为高速自旋电子学器件和电路的优良候选材料。

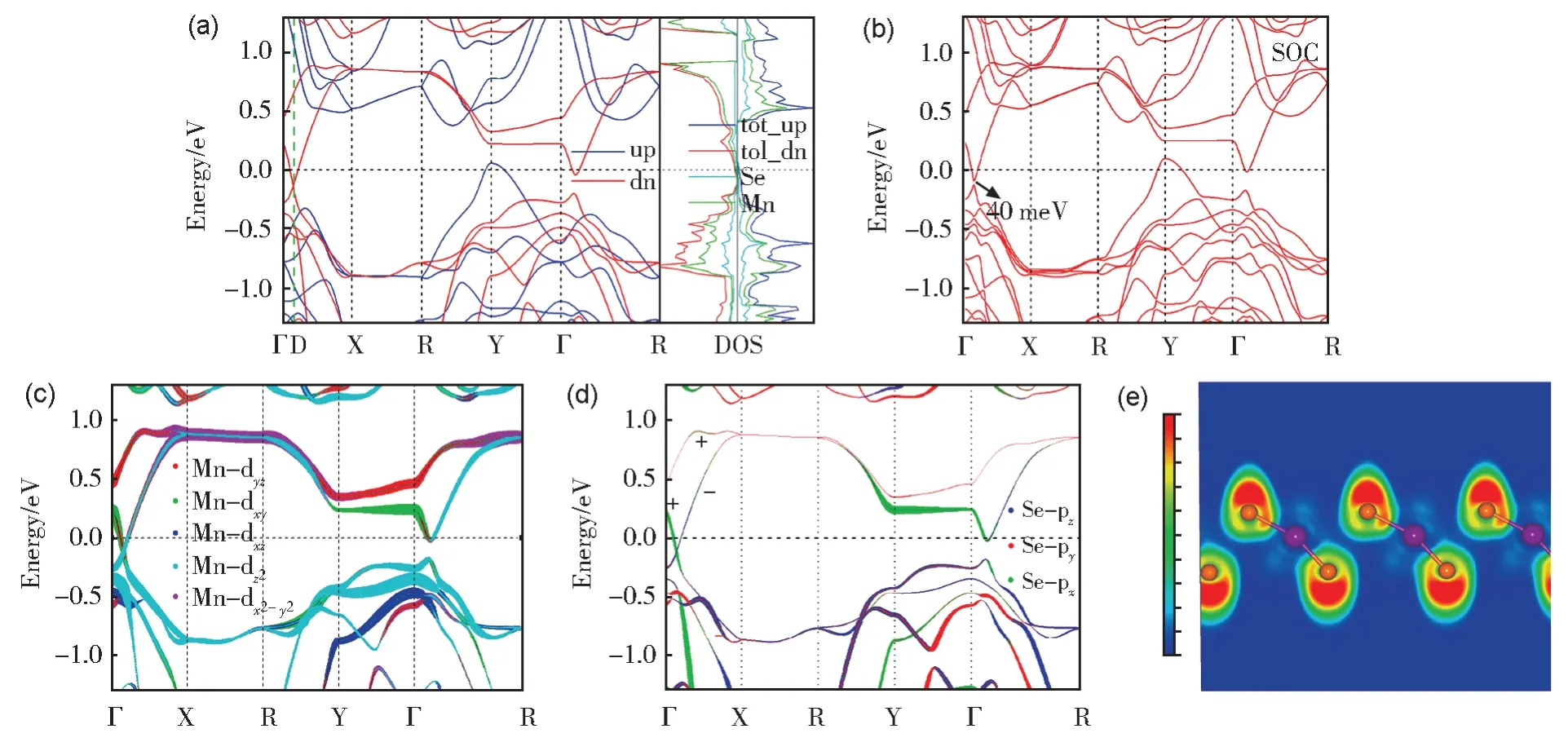
图2 （a） 无SOC的自旋极化能带结构和自旋局域态密度 （LDOS），红线和蓝线分别表示自旋向下和向上的通道；（b） 考虑SOC的能带结构；（c） 和 （d） 1T'-MnSe2中Mn-d和Se-p轨道投影能带图，（c） 表示Mn-dyz、Mn-dxy、Mn-dxz、Mn-dz2和Mndx2-y2的贡献，（d） 表示Se-px、Se-py和Se-pz的贡献，线的粗细对应于不同轨道的贡献权重；（e） 电荷局域密度图Fig.2 (a) Spin-polarized band structures and spin-resolved local density of states (LDOS) without SOC.The red and blue lines represent spin-down and spin-up channels, respectively.(b) Band structure with SOC.(c) and (d) are partial orbital projected bands for 1T＇-MnSe2.(c) represents the contribution of Mn-dyz, Mn-dxy, Mn-dxz, Mn-dz2 and Mn-dx2-y2 states, (d) represents the contribution of Se-px, Se-py, and Se-pz states, where the width of the lines corresponds to the contribution weight of the state, and (e) The electron localization function (ELF) map

为了研究狄拉克锥的原子轨道来源，图2（a） 中展示了1T'-MnSe2的总态密度和投影态密度，Mn 和Se 自旋向下的部分轨道投影能带图如图2（c）和（d）所示。可以发现，狄拉克锥周围的电子态主要由Mn 原子的d 轨道贡献，这表明电子态具有半局域轨道特性，狄拉克锥可能具有较强的关联性，并且证实了二维1T'-MnSe2属于d 态DHM。由Bader 电荷［45］可得，每个Mn 原子损失0.85 e，Se1 和Se2 原子分别获得0.37 e 和0.48 e。如图2 （e） 所示010 面电荷局域密度图可以看到电荷主要局域在Se 原子周围，证实了其电负性且说明Mn-Se 键更倾向于离子键。

众所周知，石墨烯的狄拉克锥受到C3 旋转对称性的保护。对于二维1T'-WTe2，在忽略SOC 效应的情况下，它是非对称的拓扑半金属；但在考虑W 原子的SOC 效应后，它变为非平凡的拓扑绝缘体［46］。1T'-MnSe2与1T'-WTe2属于同一空间群，1T'-MnSe2的狄拉克锥也受螺旋旋转对称 （2x） 的保护。对于1T'-MnSe2，其空间群P2_1/m的对称操作可以设置为中心反演对称矩阵I： （x，y，z） → （-x，-y，-z） 和旋转矩阵2x： （x，y，z） → （x+1/2，-y，-z）。由于2x=exp(-ik)，在ky=0 或π的螺旋线中，本征值可分为+exp(-ikx/2)和-exp(-ikx/2)。通过计算费米能级以下自旋向下通道的填充数，发现这些带被偶数填充，而穿过费米能级的金属带只存在奇数填充。假设N+，k和N-，k分别表示+exp(-ikx/2)和-exp(-ikx/2)的螺旋本征值的个数，当这两个数异号时，将在特殊的k点发生能带反转以确保系统的非平凡特性。图2（d） 中展示了费米能级附近沿 Γ-X 的1T'-MnSe2能带螺旋本征值的符号。两条螺旋线 （-X←→X 和-R←→R） 的本征值将在D 和D' （如图1 （c）） 之间发生与1T'-WTe2相同的能带反转［46］。此外，当忽略SOC 效应时，由于偏心镜像对称性x=2xI，费米能级以下约0.9 eV （图2 （a）） 的高对称路径X-R 中存在双重简并度的能带。在高对称路径X-R 中，算符x将波函数ψ转换为其时间反演算符Tψ，使得哈密顿算符的这两个本征态具有相同的本征值。

另一个有趣的现象是：在考虑SOC 效应后，DHM 的狄拉克锥表现出拓扑非平凡性。对于没有TRS 的自旋极化狄拉克锥，SOC 的引入将产生QAH 效应［20，22］。对于二维1T'-MnSe2，在引入SOC 后，在自旋向下的通道打开约40 meV 的带隙如图2（b）。这个带隙足够大，在实验中也可以被观察到，由此，二维的1T'-MnSe2可能在自旋电子器件中得到实际应用。在考虑SOC 效应后，为了证实1T'-MnSe2的拓扑特性，我们使用以下公式计算Chern 数C：

其中，可以由Kubo 公式得到Berry 曲率Ω(kx，ky)［47-48］：

其中，fn为费米-狄拉克分布函数，ψm(n)k和Em(n)是能带m(n)的布洛赫波函数和相应的本征能量；vx(y)是速度算符。图3（a）展示第一布里渊区内的Berry 曲率分布，可以看到在D 和D'点处形成两个同号的Berry 曲率尖峰。陈数是对费米能级以下所有态Berry 曲率在第一布里渊区的积分，计算得出1T'-MnSe2的Chern 数为C=-1。表明由SOC 效应打开的带隙使材料具有拓扑非平凡性，1T'-MnSe2是一种具有量子反常霍尔效应的本征Chern 半金属。图3（b） 中展示出1T'-MnSe2反常霍尔效应的电导率。量子霍尔平台位于费米能级以下约-0.1 eV，约为40 meV，宽度为-e2/h，这与计算的Chern 数（C= -1） 一致。关于QAH 另一个重要的特征是：手性边缘态受到拓扑性质保护［20，22，49］。边缘态的局部态密度如图3（c）所示。可以发现，只有一个穿过狄拉克锥带隙的价带和导带连接起来的手性边缘态，这也再次证实Chern数C= -1。

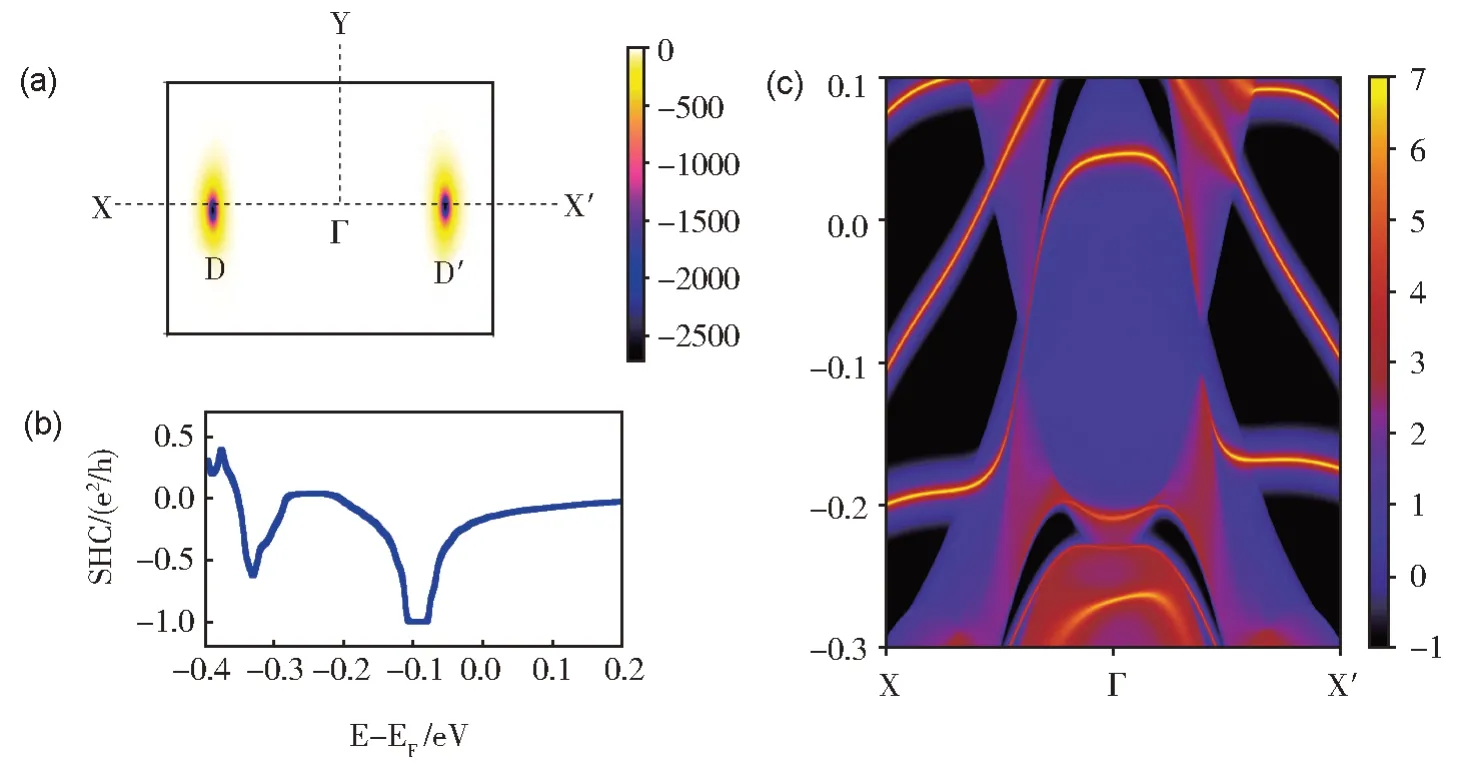
图3 （a） 1T'-MnSe2在动量空间中的Berry曲率；（b） 费米能级能量函数中的反常霍尔电导率；（c） 边缘态的局部态密度Fig.3 (a) The distribution of the Berry curvature in momentum space for 1T＇ -MnSe2; (b) Anomalous Hall conductivity in function of the energy of the Fermi level; (c) The local density of states of edge states

对于拥有3d 轨道的 TM 化合物，如3d 过渡金属氧化物Mott 绝缘体，3d 轨道的强关联效应对其电子态有很大影响。我们采用约束随机相位近似 （cRPA） 估算Mn-3d 的Hubbard 参数为UMn-3d= 0.36 eV，用Wannier 的投影函数来构造3d 轨道的相关子空间，并且在极化计算中把3d轨道的影响排除在外。为了更进一步揭示强关联效应对1T'-MnSe2电子结构的影响，我们采用电子-电子 （e-e） 相互作用更强的U= 1.0 eV 进行了GGA+U 计算，能带结构和LDOS 如图4，可以看到1T'-MnSe2仍保持DHM 的特征。这说明Hubbard 参数对1T'-MnSe2的DHM 和QAH 特性影响不大。

图4 当Hubbard U = 1.0 eV时，不考虑SOC的能带结构和自旋局域态密度 （LDOS）Fig.4 The band structure and spin-associated local density of states (LDOS) without SOC under Hubbard U = 1.0 eV

3 结论

采用第一性原理方法，本文提出铁磁态下的1T'-MnSe2是d 态DHM。通过计算其结合能、形成能和声子谱充分证实了结构稳定性。进一步考虑SOC 效应时，体系在狄拉克点自旋向下通道中打开了约40 meV 的带隙，其具有非零Chern 数 （C= -1） 和无间隙手性边缘态均证实体系独特的拓扑非平凡性。霍尔电导计算表明，两个分裂的狄拉克锥周围的Berry 曲率均贡献单位电导的一半。这些都证实铁磁态1T'-MnSe2是一种Chern 半金属。1T'-MnSe2拥有较大的带隙并存在自旋极化狄拉克态，使其成为可以在二维自旋电子器件中实现QAHE的备选材料。