面向区间型数据的不同区间核SVM分类模型

祁晓博，宋金玉，史颖，3，亓慧，穆晓芳

（1.太原师范学院 计算机科学与技术学院，山西 晋中 030619；2.太原师范学院 数学与统计学院，山西 晋中 030619；3.山西大学 计算机与信息技术学院，山西 太原 030006）

0 引言

大数据时代的到来，不仅带来了数据量的指数型增长，还使数据的复杂性与日俱增。区间型数据（Interval-valued data，IVD）是一种常见的定量符号数据，它的特点是每个属性特征都不再是一个数值，而是一个区间范围。一般来说，区间型数据包含更多的数据内在结构特征，因此相较于传统数值型数据，更有利于揭示隐含在数据内部的变化规律。然而区间型数据的表现形式较为特殊，使得一般分类方法无法直接对其进行处理，除非如同区间型数据的主成分分析［1-2］、判别分析［3-5］、回归分析［6-9］和聚类分析［10-12］等其他分析方法，在使用前对它进行合理的数值表示。表示后的区间型数据也并不十分完美，要么损失大量信息，要么特征数是原始数据的2 倍，这些不足不仅会影响分类器的分类性能和效果，还会增加内存存储和时间复杂度。为了使区间型数据在分类过程中克服这些不足，分类方法的选择十分重要。

分类问题是机器学习领域中一项重要任务，它的目的是将已有数据中学习到的规律用于新数据的预测和分析，为人们的决策提供理论指导。主流的分类方法可以分为单一分类方法和集成分类方法。神经网络分类、决策树分类、K 近邻分类及支持向量机分类（Support Vector Machine，SVM）等是常用的单一分类方法。尽管这些单一分类方法发展迅速，但实际生活中的一些复杂问题仍然无法用这些方法得到有效解决，因此集成分类方法应运而生，其中Bagging 系列和Boosting 系列方法是集成分类的典型。目前不管是单一分类方法还是集成分类方法都是针对传统数值型数据的，面对区间型数据时，这些方法就显得有些力不从心。

相较于其他分类方法，支持向量机是一种运用核函数将原始空间样本投影到高维特征空间进行分类的算法，而核函数最早且最成功的应用也是在支持向量机上。由于核函数是基于结构风险最小化原则的，因此以它为核心的支持向量机同样具有核函数的优势，在理论基础和泛化能力方面表现十分出色。常用的核函数有多项式核、线性核、高斯核及Sigmoid 核［13］。一般来说，不存在万能核函数，实际问题中人们往往根据具体的应用背景构造新的核函数［14］。Ozer 等［15］将切比雪夫多项式推广成向量形式，并由此构造切比雪夫核函数用于支持向量机分类。此外Zhang 等［16-17］提出的基于洛伦兹函数构造的核函数、勒让德核函数及Zhang 等［18］的最优松弛因子核函数极大丰富了核函数的种类。

上述基于不同核函数的支持向量机方法对传统数据是有效的，但是并不能很好地完成区间型数据的分类。鉴于此，文献［19］中在高斯核基础上构造出高斯区间核函数，提出的高斯区间核SVM 分类模型（Support Vector Machine Based on Sigmoid Interval Kernel，GIK_SVM）能更好地适应区间型数据的分类，且分类结果较好。核函数的种类虽然在不断地增长，但是仍存在以下两方面问题：一是核函数的性能总是相对具体数据集而言的，二是核参数优化的可行性要在考虑范围内。针对这两个问题，本文提出了面向区间型数据的不同区间核SVM 分类模型，除包含之前的GIK_SVM 外，该方法还提出了适用于区间型数据的线性区间核、多项式区间核和Sigmoid 区间核，并构建相应的分类模型，即线性区间核SVM 分类模型（Support Vector Machine Based on Linear Interval Kernel，LIK_SVM），多项式区间核SVM 分类模型（Support Vector Machine Based on Polynomial Interval Kernel，PIK_SVM），Sigmoid 区间核SVM分类模型（Support Vector Machine Based on Sigmoid Interval Kernel，SIK_SVM）。在人造数据集和真实数据集上的实验结果表明不同区间型数据集适用不同的区间核函数SVM 分类模型。

1 区间核SVM分类模型

在支持向量机中，核函数的类型及其参数直接决定了SVM 的学习能力和泛化能力。由于区间型数据结构的特殊性，SVM 中常用的核函数不能直接用于区间型数据。在高斯区间核［19］基础上，考虑到实际问题中样本数据的特征往往未知，本文提出不同的区间核，使其能够直接用于区间型数据并取得较好的分类精度。

1.1 区间型数据矩阵

二元区间数在表示属性内涵的基础上，能够有效克服由于模糊性而带来的数值上的不确定性，具体定义如下［20］：

定义1（二元区间数）设R 表示实数集，对任意u-，u+∈R 且u-≤u+，记

称u=[u-，u+]为一个标准的二元区间数。其中，u+为上极限，称为二元区间数的大元，u-为下极限，称为二元区间数的小元。

性质1对任意u∈I(R)（全体二元区间数的集合），如果u-=u+，则u=[u-，u+]退化为一个普通的实数，即u=u-=u+，故R ∈I(R)。所以区间数是实数的推广。

根据二元区间数的定义，给出区间型数据矩阵、区间中值与区间半径的定义。

定义2（区间型数据矩阵）设区间型数据，则U=[uij]为n×p区间型数据矩阵，即

定义3（区间型数据中值）设区间型数据，则区间型数据uij的中值为

定义4（区间型数据半径）设区间型数据，则区间型数据uij的半径为

1.2 区间核构造

核方法是机器学习中解决非线性问题的一种重要技术，它通过核函数描述特征空间向量间的内积，避免非线性映射的显示表达。根据区间型数据的定义以及高斯区间核的构造方法，本文相继提出线性区间核、多项式区间核和sigmoid 区间核。对于任意两个区间型样本和，三种区间核构造方法如下：

（1）线性区间核：

（2）多项式区间核：

（3）Sigmoid 区间核：

其中，上述三种核中的参数α表示意义相同，α∈[0，1]，是区间型数据的调节因子，使区间中值与区间半径对样本的相似性度量达到有效折中。当α=1 时，三种区间核只考虑区间中值；当α=0 时，三种区间核只考虑区间半径；当α∈(0，1)时，区间中值与区间半径可以做到有效平衡。多项式区间核与Sigmoid 区间核中的参数γ、r也相同，γ为核函数系数，r为核函数独立项。多项式区间核中的参数d为阶数，决定多项式的最高次幂。

1.3 算法的主要步骤

设区间型数据集T={(U，Y)}，U为区间型数据矩阵，Y为分类标签。本文提出的区间核SVM 分类模型的主要思想是：首先计算出区间型数据的区间中值与区间半径，然后根据数据集的分布特征构造合适的区间核矩阵，最后用构建的区间核SVM 分类模型进行分类。IK_SVM 算法的主要步骤如下：

输入：区间型数据矩阵U，区间核参数γ，r，d，调节因子α；

输出：分类精度acc。

①根据公式（3）和（4）分别计算出区间中值和区间半径；

②构造区间核矩阵并建立相应的区间核SVM 模型：

Switch（kernel）｛

case ‘Linear’：构造线性区间核矩阵并建立线性区间核SVM 分类模型LIK_SVM；

case ‘Poly’：构造多项式区间核矩阵并建立多项式区间核SVM 分类模型PIK_SVM；

case ‘RBF’：构造高斯区间核矩阵并建立高斯区间核SVM 分类模型GIK_SVM［19］；

case ‘Sigmoid’：构造Sigmoid 区间核矩阵并建立Sigmoid 区间核SVM 分类模型SIK_SVM；｝

③在数据集上进行训练和测试，计算分类精度acc；

④算法结束。

1.4 时间复杂度分析

对于n×p维区间型数据矩阵，n为样本个数，p为特征数。

线性SVM 的时间复杂度为O(np)，非线性核SVM 的时间复杂度一般是在O(n2p) 与O(n3p)之间。由于α将区间中值与区间半径调节为一个整体，特征维数并未增加，所以LIK_SVM 的时间复杂度为O(np)，PIK_SVM 与SIK_SVM 的时间复杂度也在O(n2p)与O(n3p)之间。

2 实验结果与分析

2.1 实验数据与实验设计

本文实验采用4 个人造数据集和2 个真实数据集。为了便于比较，数据集与文献［19］相同。其中Ds1、Ds2、Ds3 和Ds4 是人造数据集，构造方法与文献［19］一致，由种子数据生成，构造公式为[z-r，z+r]，z是根据正态分布生成的种子数据，r是从均分布中提取的宽度。数据集的类别主要由种子数据的位置区分，图1 为4 个人造数据集上随机选取200 个数据的分布图，红色和蓝色分别为两类不同的区间型数据。HS_Ds 和TB_Ds 是真实数据集，来源于“Reliable Prognosis”站点（rp5.ru）提供的气象数据［21］。实验数据详见表1。为了保证方法的稳定性，本文的每个实验都是10 次实验结果的平均值。实验部分均在MATLAB R2014a 平台下实现，所用计算机环境为Intel（R） Core（TM）i7-4790，3.60 GHz，内存8 GB，64 位操作系统。

图1 人造数据集的分布Fig.1 Distributions of synthetic datasets

表1 实验数据集Table 1 Experimental datasets

本文首先验证参数α和γ分别对所提LIK_SVM、PIK_SVM 和SIK_SVM 的影响，多项式区间核和Sigmoid 区间核参数r都设为默认值0，多项式区间核参数d为默认值3。随后将上述三种方法与GIK_SVM 方法进行分类精度的比较，说明不同区间型数据集适用不同的区间核函数SVM 分类模型。

2.2 实验结果及分析

（1） 调节因子α的影响

本实验中，γ设为默认值，α在[0，1]之间取值，验证调节因子α对分类精度的影响并确定三种方法在各数据集上的最优值。LIK_SVM、PIK_SVM 和SIK_SVM 在各个数据集上的分类精度随α变化情况如图2 所示。图中清晰显示了α对三种分类模型在不同数据集上的影响。LIK_SVM 在6 个数据集上基本呈上升趋势，在α=0.01 时，上升趋势尤为明显，Ds1 和TB_Ds在α=1 处有下降。PIK_SVM 除了在HS_Ds 上起伏较大外，在其余5 个数据集上也基本呈上升趋势。Ds1-Ds4 在α=0.25 处，有明显上升，在0.75 处达到最优。SIK_SVM 在TB_Ds 上变化不大，在另外5 个数据集上呈上升趋势，α=0.01 处，起伏最大。TB_Ds 在α=0 时，达到最优值。SIK_SVM 在真实数据集上的结果不是很理想，HS_Ds 和TB_Ds 的分类精度最高在50%左右。

图2 调节因子α的影响Fig.2 Influence of adjustment factor α

为了更好地描述不同方法随调节因子α在各个数据集上的变化，每种方法在各数据集上的最优α值见表2 所示。表中可以看出不同的数据集分布各不相同，三种方法随α值的变化也不尽相同，最优α值基本分布在0，1 之间，其中SIK_SVM 方法在TB_Ds 上略有不同，在α取0 时，分类精度最大，根据公式（7）知此时区间型数据只保留了区间半径，没有区间中值。

表2 各方法的最优α值Table 2 Best α of each method

（2） 参数γ的影响

由于LIK_SVM 没有参数γ，PIK_SVM、SIK_SVM 和GIK_SVM 在各个数据集上的分类精度随γ变化情况如图3 所示。PIK_SVM 和SIK_SVM 选取表2 中最优α值，GIK_SVM 使用文献［19］的最优α值。图中可以看出不同的γ值对分类精度的影响很大。在Ds1 和Ds2 上，GIK_SVM 的变化较为平缓。PIK_SVM 在γ=0.25 时，上升变化明显，分类精度超过GIK_SVM，随后趋于平缓。SIK_SVM 开始与GIK_SVM 相差不大，在γ=10 时开始下降。在Ds3 和 Ds4 上，GIK_SVM 在 PIK_SVM 和SIK_SVM 之上，且变化不大。PIK_SVM 在γ=0.1 处有小幅上升，随后上升幅度减少；在γ=50 时有下降，随后有小幅波动。在HS_Ds 上，GIK_SVM 在γ=10 时下降，但分类精度仍优于PIK_SVM 和SIK_SVM。PIK_SVM 波动较大，但整体呈下降趋势。SIK_SVM 在γ=0.5 处明显下降，随后较平缓。在TB_Ds 上，PIK_SVM虽有波动，但整体优于GIK_SVM 和SIK_SVM。GIK_SVM 整体呈下降趋势。SIK_SVM 则起伏不大，较为平缓。参数γ对分类精度确有一定的影响，本文不对γ做详细优化，主要关注调节因子α的有效性。从实验中可以看出，γ在2 之前已有较好的分类精度。

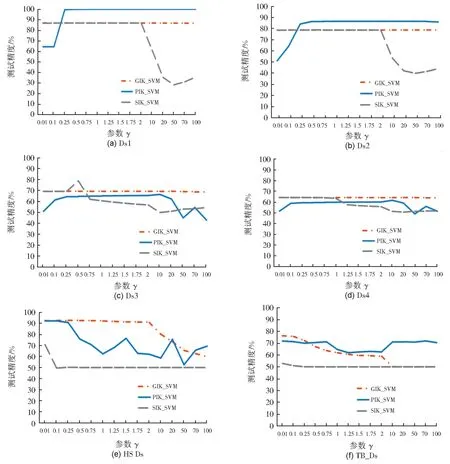
图3 参数γ对测试精度的影响Fig.3 Influence of parameter γ on test accuracy

为了更好地描述不同方法随参数γ在各个数据集上的变化，每种方法在各数据集上的最优γ值见表3 所示。表中可以看出不同的数据集上最优γ值不尽相同。GIK_SVM 的最优γ值多集中在0.25 上，只有TB_Ds 在0.01 处最优。PIK_SVM 的最优γ值相对较大，Ds1-Ds4 上的最优值都大于等于2，在HS_Ds 和TB_Ds 上的最优γ值小于1。SIK_SVM 的最优值也都小于1，Ds2 和Ds3 上最优值为0.5，HS_Ds 和TB_Ds为0.01，另外两个数据集上的最优γ值分别为0.25 和0.1。（3） 与文献［19］中GIK_SVM等方法的比较

表3 各方法的最优γ值Table 3 Best γ of each method

将LIK_SVM、PIK_SVM 和SIK_SVM 与文献［19］中的GIK_SVM、IM_SVM 和IBV_SVM方法进行比较。参数r和d都设为默认值，α和γ分别选取表2-3 以及文献［19］中各个数据集上的最优值，六种方法在各数据集上的分类精度如表4 所示。在Ds1 和Ds2 上，PIK_SVM分类效果最优，在Ds3 上，SIK_SVM 分类效果最好，在Ds4、HS_Ds 和TB_Ds 上，则是GIK_SVM 分类精度最高。由图1 知，Ds1 和Ds2 中两类数据分布紧密，但是界限较为清晰，此类分布的数据，PIK_SVM 具有更好的处理能力。Ds3 和Ds4 混合重叠较多，数据较分散，SIK_SVM 在这类分布的数据上具有较好的分类效果。Ds4 上的最优结果虽然是GIK_SVM方法，但是LIK_SVM、SIK_SVM、IM_SVM 和IBV_SVM 分类精度与其相差不大。在HS_Ds和TB_Ds 上，GIK_SVM 表现最优，LIK_SVM 和PIK_SVM 次之，IM_SVM 和IBV_SVM 又略低，而SIK_SVM 分类精度最低，只有50% 左右。表中可以反映出不同分布的数据集上最优结果主要集中在GIK_SVM、PIK_SVM 和SIK_SVM 上。

表4 六种方法精度比较Table 4 Comparison of accuracy among six methods

综上所述，中值-半径构造的区间核SVM模型整体比中值与边界值模型分类性能佳，GIK_SVM、PIK_SVM 和SIK_SVM 在一些数据集上均能达到最优值，GIK_SVM 最优值最多，LIK_SVM 方法在6 个数据集上虽没有最优值，但其分类精度在各数据集上居于中间水平，不是最高也不是最低。在6 个数据集上，PIK_SVM 的平均分类精度最高，GIK_SVM 和LIK_SVM 虽低于PIK_SVM，但其相差不大。SIK_SVM 虽在Ds3 上的分类精度明显高于其余五种算法，但在两个真实数据集上的结果较差。实验说明不同分布的区间型数据集适用不同的区间核函数。

3 结论

综合考虑区间型数据的特殊结构及其数据不同分布的影响，本文提出面向区间型数据的不同区间核SVM 分类模型。通过调节因子对区间中值与区间半径进行有效折中，相较于中值与边界值的分类模型，中值-半径构造的区间核明显优势更大。本文方法将这些区间核函数集成在一个分类模型中，之后可以根据数据集类型选择区间核函数进行分类。实验结果表明，区间核SVM 分类模型更适用于区间型数据的分类处理，其中不同分布的区间型数据集选择合适的区间核分类模型也是非常重要的。

不同数据集上的最优分类精度由不同区间核SVM 模型得出，故几类区间核的分类性能与数据集的分布是相关的，这将是未来研究工作的一部分重要内容，另外，适用于更多分布的多种区间核函数构造方法也将是一项重要研究内容。