Rabi和Ramsey原子光谱最优测量点的选取

吴嘉瑜，张秀荣，李卫东

（1.山西大学 理论物理研究所，山西 太原 030006；2.山西大学 物理电子工程学院，山西 太原 030006；3.深圳技术大学 工程物理学院，先进材料诊断技术中心，超强激光与先进材料技术深圳重点实验室，广东 深圳 518118；4.广东省量子科学技术与工程重点实验室（南方科技大学），广东 深圳 518055）

0 引言

原子钟在全球定位系统、精确打击武器、信息高速公路等方面起着关键的作用［1-4］。它的精度是反映国家战略竞争力的重要标志之一［5］。目前，最先进的原子钟利用单离子的光跃迁［6］或者是光晶格中原子云的跃迁谱线［7］，其不确定度可达10-18至10-19量级［8-9］。而各种原子钟一般是通过Rabi 或Ramsey 过程，将本地振荡器的频率锁定到量子参考体系（通常是两能级原子）的跃迁频率上［10］。在不考虑其他因素的条件下，参考体系跃迁谱线的线宽越窄，原子钟的性能越好［11-14］。但是在实际的光谱测量中，由于实验条件的限制和外界因素的干扰，一般会根据光谱的对称性，测量失谐量大小相同的两点处原子的跃迁几率，来确定跃迁频率。这样往往不能测量得到完整Rabi 光谱，因而不能准确地反映光谱的半高全宽，导致量子参考体系的品质因数降低，因此光谱测量点的选取决定了原子钟的精度［11］，而Fisher 信息值的大小与最佳测量点有关。

在测量中，通常认为测量结果仅能提供被测量事件的近似情况，即仅能无限接近真值［15］。变量的统计估计存在一个最低的极限，这个极限就是Cramer-Rao 下界（CRB），其与Fisher 早些年提出的Fisher 信息有直接关系——Cramer-Rao 下界至少大于Fisher 信息的倒数［13］。在量子测量中，如果人们考虑所有可能的量子测量条件，此时的Fisher 信息的最大值被称为量子Fisher 信息［16］。Fisher 信息被公认为是一种标度测量精度的有效物理量，广泛地应用于精密测量领域，利用量子Fisher 信息对于重力加速度测量精度的评估、对于弱测量参数的评估等都取得较为满意的结果［16-20］。因此，我们将量子Fisher 信息引入Rabi 光谱和Ramsey 光谱最优测量条件的研究，以提高原子钟的精度。

本文首先介绍二能级原子模型、Rabi 振荡和Ramsey 过程以及Rabi 和Ramsey 光谱；接着介绍量子投影方式下的量子Fisher 信息，以及利用Rabi 光谱和Ramsey 光谱，讨论系统参数对量子Fisher 信息的影响，得到最优测量条件；最后一部分是总结。

1 Rabi光谱和Ramsey光谱

1.1 Rabi振荡和Rabi光谱

c1(t)，c2(t)是任意时刻体系处于的几率幅，在电偶极近似和旋波近似下，体系的哈密顿量可表示为

其中2b为Rabi 频率，代表电磁场和系统的耦合强度，ω是电磁场频率。通过解析求解关于c1(t)，c2(t)的微分方程可以得到波函数的通解

其中，A和B为待定参数，由初态条件决定；，失谐量Δ=ω0-ω是原子频率和振荡场频率的差值。

如果体系的初态为基态，则系统在任意时刻的波函数为

其中，cosθ=Δ/a，sinθ=2b/a。我们可以知道任意时刻体系处于态的概率为

由（4）式可知，布居率P2随时间做周期振荡，此即Rabi 振荡。在图1（a）中，我们展示了不同失谐时的Rabi 振荡，其振荡幅度和周期均不相同，共振时（Δ=0）Rabi 振荡的幅度最大，周期最长。

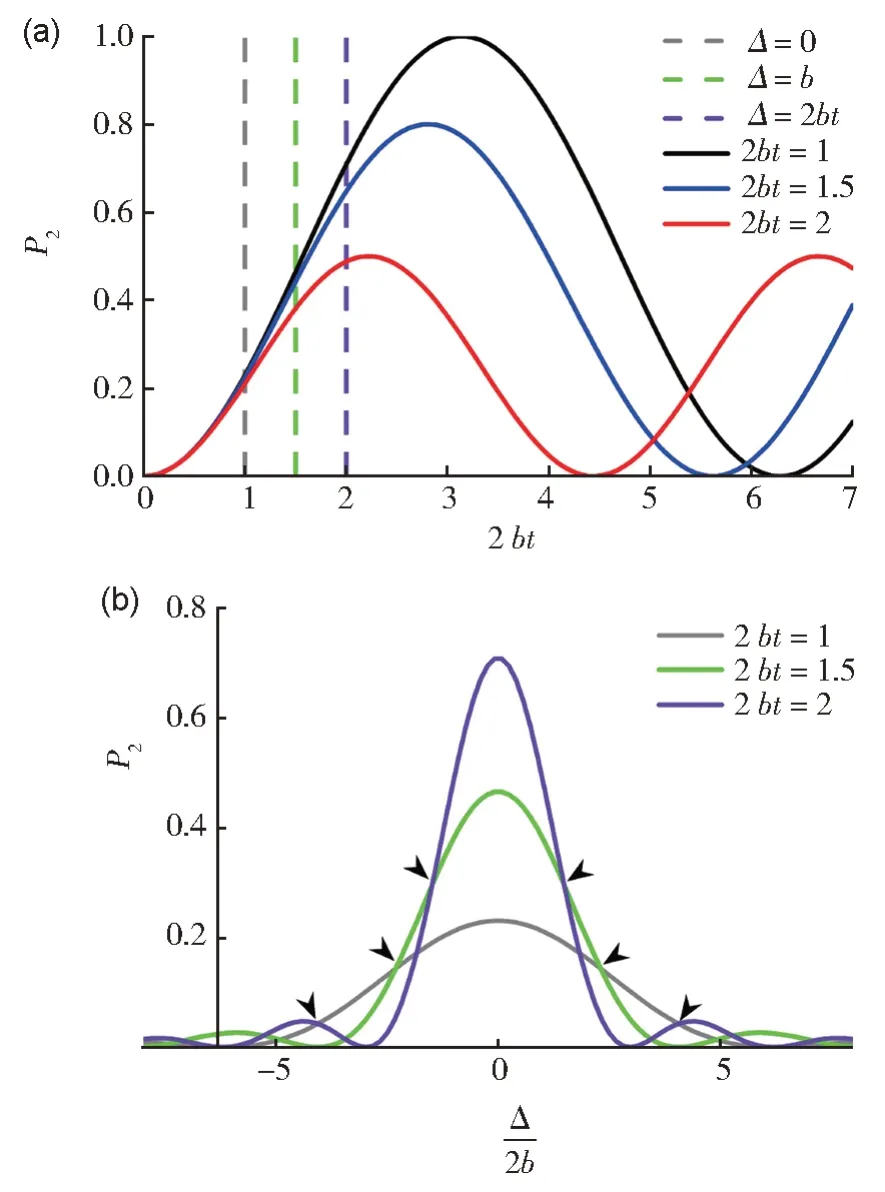
图1 （a）Rabi振荡；（b）Rabi谱Fig.1 (a) Rabi oscillation;(b) Rabi spectrum

对于确定的时间t，布居率P2随失谐量Δ 变化的图像称为Rabi 光谱，如图1（b）所示，选取了一些特定时刻的Rabi 光谱（所选时刻在图1（a）中用虚线标记）。在t＜π/(2b)的范围内，所有Rabi 谱线均在共振处占据率P2取得最大值，同时t越大与之对应的Rabi 光谱在共振处的幅度越大。若在t＞π/(2b) 的某些时刻测量，则最大峰值不在共振处取得，共振峰幅度低于其他峰，但谱线仍是对称的。测量时我们需要确保最大峰值出现在共振处，因此，最佳测量时刻是在π/(2b)前，且时刻愈晚愈佳。

1.2 Ramsey技术和Ramsey光谱

原子钟参考体系的制备除了Rabi 激发，还有Ramsey 干涉仪。Ramsey 干涉仪的过程也被称为分离振荡场技术［21-22］，具体过程可分为三个阶段：（1）对原子体系施加π/2 脉冲，即电磁场作用时长为τ=π/(4b)；（2）关闭电磁场，让体系自由演化一段时间，称为间歇时间T；（3）再次施加电磁场，持续时间τ以后测量跃迁谱线。当系统的初态是基态，即c1(0)=1、c2(0)=0，根据式（2）可以得到系统在任意时刻的波函数。在t=T+2τ时刻，系统处于态的概率为

对于Ramsey 过程，布居率P2随失谐量Δ 变化的图像称为Ramsey 光谱，如图2 所示，（a）、（b）分别为T=5/(2b)，T=10/(2b) 时的Ramsey 谱。通过对比图1（b）和图2，可见在相同外场条件时，Ramsey 光谱比Rabi 光谱的线宽更窄，而且间歇时间越长，Ramsey 谱线线宽越窄。

图2 Ramsey谱线 （a） T=5/（2b）； （b） T=10/（2b）Fig.2 Ramsey spectrum (a) T=5/(2b); (b) T=10/(2b)

2 量子Fisher信息在光谱中的应用

2.1 量子Fisher信息在Rabi光谱中的应用

在利用Rabi 光谱和Ramsey 光谱进行测量时，实验系统的跃迁谱线半高宽越窄，原子钟系统的稳定度越高。如前所述，实验在失谐量大小相同的两点处测量原子的跃迁几率时，我们希望用量子Fisher 信息指出最佳测量点。由于系统是一个二能级原子体系，符合量子投影测量，此条件下的Fisher 信息值公式为［18，23］

量子Fisher 信息是Fisher 信息的最大值，实验精度是量子Fisher 信息值的倒数，所以量子Fisher信息值越大，测量精度越高。

依据公式（6），在Rabi 谱中Fisher 信息公式的具体形式为

不同时刻Rabi 光谱的Fisher 信息随失谐量的变化如图3 所示，随着时间的推移，量子Fisher 信息值越来越大，测量精度越来越高，因此与分析线宽得到的结论一致，相互作用时间越接近π/(2b)，测量精度越高。

图3 不同t时，Fisher信息随失谐量变化曲线Fig.3 Variation curve of Fisher information with detuning at different time

从图3 中可以看到，最大Fisher 信息值即量子Fisher 信息出现在共振峰的侧腰位置，其位置在图1（b）中用箭头标出，此时对应的失谐量是实际光谱测量时的最佳位置。量子Fisher 信息对应失谐量随时间的变化趋势，从图4 可以更直观地观察到，有助于实验时更快找到最佳测量位置。

图4 Rabi光谱量子Fisher信息对应失谐量与时间关系Fig.4 Relationship between the detuning and time corresponding to quantum Fisher information of Rabi spectrum

因此，通过分析Rabi 光谱的量子Fisher 信息，能够得出Rabi 光谱的最优探测条件是相互作用时间接近π/(2b)，并且可以确定出最优测量位置。

2.2 量子Fisher信息在Ramsey光谱中的应用

我们将图2 中Ramsey 光谱的共振峰单独取出，如图5 所示，随着间歇时间的增大，可以更直观地看到Ramsey 光谱共振峰的线宽是逐渐减小的，意味着可以由间歇时间控制Ramsey 光谱谱线的精度。对于Ramsey 光谱，由于共振处占据率恒等于1，所以此时不再是一个两输出测量，公式（6）失效；但是对于Ramsey 光谱的其余部分，仍然符合投影测量的条件，所以可用（6）式计算共振峰半高宽处的Fisher 信息，此时公式（6）变为

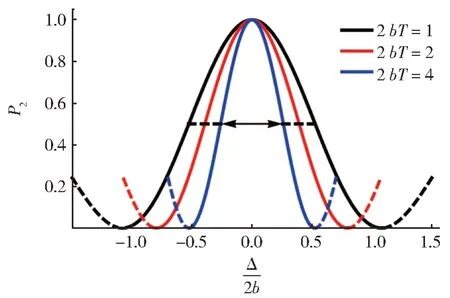
图5 不同T时，Ramsey光谱的共振峰Fig.5 Various curves of resonance peak of Ramsey spectrum with different interval time T

其中d/2 是半高宽。不同T的Ramsey 光谱共振峰半高宽处的Fisher 信息值F(d/2)如表1 所示，随着T的增大，半高宽处的Fisher 信息值也逐渐增加。与图3 对比可知，Ramsey 光谱半高宽处的Fisher 信息值比Rabi 光谱的量子Fisher 信息值更大，代表着Ramsey 光谱具有更高的测量精度。

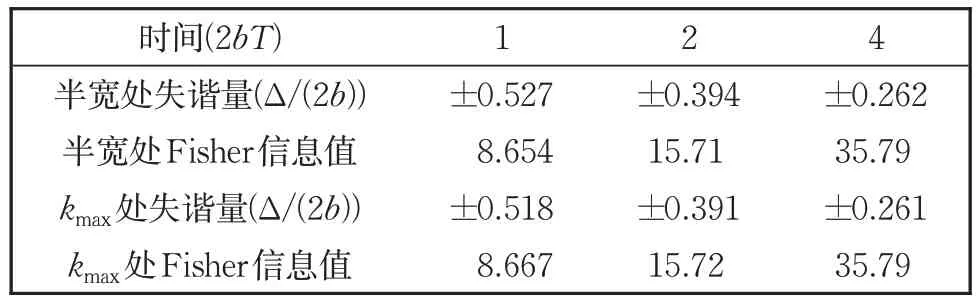
表1 不同间歇时间，Ramsey光谱共振峰半宽处与斜率最大处Fisher信息比较Table 1 Comparison of Fisher information at the half width of the resonance peak and the maximum slope of Ramsey spectrum at different interval time

在表1 中，我们还依次求取不同T时共振峰斜率最大处（表中用kmax表示斜率最大）的Fisher 信息值，与半高宽处的相应数据比较，斜率最大处Fisher 信息比半高宽处大，但是随着T的增加，二者差距越来越小。所以可以认为Ramsey 谱线半高宽处的Fisher 信息近似为量子Fisher 信息，其失谐量就是最佳测量位置。

通过上述分析可知，在相同外场条件下，测量Ramsey 光谱可以获得比Rabi 光谱更高的实验精度，且间歇时间越大，精度越高；对于Ramsey 光谱，半高宽处可作为最佳测量点。

3 结论

本文通过解析求解与电磁场作用的二能级原子体系，基于Rabi 光谱和Ramsey 光谱计算了量子投影方式下的量子Fisher 信息值。由量子Fisher 信息可以得到，测量Rabi 谱时，最佳测量时间接近π/(2b)，并且指出最佳测量位置与作用时间的关系。在相同条件下，Ramsey 光谱通过延长两腔之间的间歇时间，较Rabi 光谱进一步增加了场和原子的作用时间，谱线的Fisher信息值更大，精度更高，且可以将共振峰半高宽处选作最佳测量位置。所以，将量子Fisher信息引入光谱测量，为原子钟精度的提高提供一种新的思路和方法，具有实用价值和进一步研究的意义。