等差等比数列任意三项(数列之和)的等量关系及应用

广东省惠州市华罗庚中学(516000) 代 军

文[1] 利用等差数列求和公式Sn=An2+Bn的特性, 用待定系数法证明了任意的n,p,q∈ N+, 有成立. 但这种方法计算量大,不利于把握与进一步学习. 下面给出另一种简洁的证明方法.

一、引理

平面向量三点共线定理: 若O为平面上任意一点,则A,B,C三点共线的充要条件是.

二、等差数列前n项和性质的另证

三、结论1 的推广及延伸

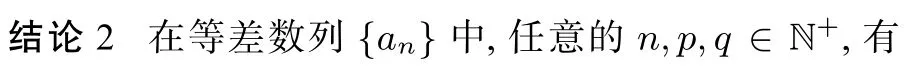
四、应用举例

注从上面的证明可以看到,结论2 和结论3 具有很好的对偶关系,而结论1 和结论4 则没有这种关系,实际上,这是我们考虑的重点不同所致, 本文的重点是探讨等差数列(或等比数列)任意三项an,ap,aq(或者Sn,Sp,Sq)之间的直接等量关系(而非对偶关系). 实际上,根据等差数列与等比数列之间的对偶关系,即加法对应乘法,减法对应除法,乘法对应乘方,除法对应开方,由结论1 是不难得到例4 的结果的,这也正是文[2]的成果之一,有兴趣的读者可以参考文[2]的具体证明,此处省略.