一道椭圆中两直线斜率之积为定值试题的探究与推广
2023-06-03重庆市长寿中学401220
中学数学研究(广东) 2023年9期
重庆市长寿中学(401220) 田 鹏
1. 试题呈现
试题(安徽省示范高中培优联盟2022 年秋季联赛第21题)如图1,A,B为椭圆的左,右顶点,焦距为,点P在椭圆E上,直线PA,PB的斜率之积为.
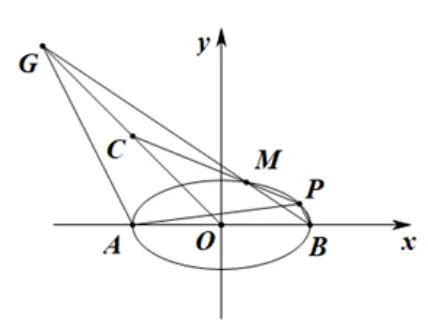
图1
(1)求椭圆E的方程;
(2) 已知O为坐标原点,点C(−2,2),直线PC交椭圆E于点M(M,P不重合),直线BM,OC交于点G. 求证:直线AP,AG的斜率之积为定值,并求出该定值.
试题第(1)问考查椭圆方程的求法,属于基础知识. 由直线PA,PB的斜率之积为,以及焦距为,不难求得椭圆E的方程为. 第(2)问设计巧妙,结论优美,背景丰富. 条件中涉及的点、线位置关系较多,具有一定的综合性. 能有效考查学生的直观想象,逻辑推理及数学运算等数学核心素养. 本文重点探究第(2)问.
2. 解法探究



3. 拓展探究


如果A,B不是椭圆的左、右顶点,而是椭圆上任意关于原点对称的两点,结论是否成立? 经过研究,有下述定理2.
定理2如图2, 已知O为坐标原点,椭圆,A,B是椭圆E上关于原点对称的两点. 椭圆E在点A处的切线为l,点C是l上的任意一点(异于点A). 点P在椭圆E上,直线PC交椭圆E于点M(M,P不重合). 直线BM,OC交于点G,则直线AP,AG的斜率之积为定值,且AG//PB.
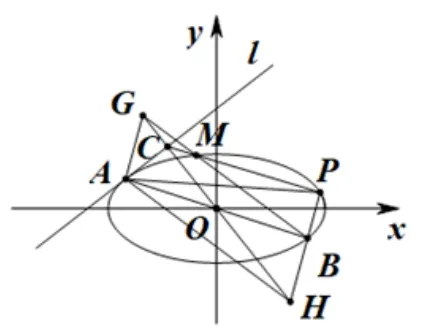
图2



4. 结语
文章立足于一道模拟试题的解法,挖掘试题背景,并将结论推广到一般的椭圆和双曲线中,得到了定理1-3. 在解析几何的教学过程中,教师要善于启发学生运用类比思想和特殊到一般的思想发现新结论,帮助学生理清试题的来龙去脉,培养学生勇于数学探索的科学精神,不断提高学生的数学综合能力.
