具有饱和发生率的网络蠕虫病毒模型分析

王瑞玲, 薛亚奎

(中北大学数学学院, 太原 030051)

近年来,随着生活水平的提高,手机、电脑等移动设备也日益普及.这些移动设备在为生活带来便利的同时,也遭受着网络蠕虫病毒的攻击,恶意蠕虫病毒的快速传播对网络安全造成了严重威胁．

准确地分析蠕虫病毒在移动网络中的动态行为已经成为一个值得关注的研究课题,许多研究人员提出了不同的数学模型[1-4].文献[1-2]考虑了隔离策略(即切断感染设备与其他设备的连接),文献[3-4]考虑了接种疫苗策略(即安装有效的杀毒软件),这两种策略都有利于降低蠕虫病毒对移动设备的攻击程度.对网络蠕虫病毒模型的研究表明,发生率在病毒传播方面起着决定作用.随着易感设备或感染设备数量的增加,发生率趋于饱和水平,在这种情况下,双线性发生率[5-6]似乎是不合理的.因此,本文考虑了饱和发生率[7-8],其系统模型为:

(1)

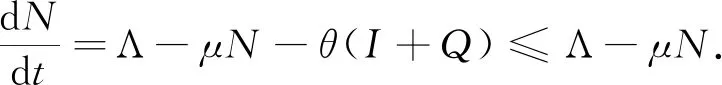
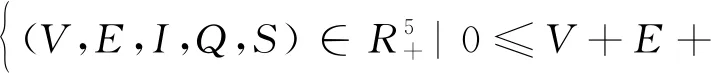
中研究系统(1)．

1 平衡点和基本再生数

集合Ω是系统(1)的正不变集.通过计算可知系统(1)的无病平衡点:

P0=(V0,E0,I0,Q0,S0)=

(2)

利用下一代矩阵法,计算基本再生数R0的表达式[10]如下:

R0=ρ(FV-1)=

(3)

定理1当R0>1时,系统(1)在Ω内存在唯一的地方病平衡点P*=(V*,E*,I*,Q*,S*)．

证明令系统(1)的方程右端均等于0,可得

因此当R0>1时,V*,I*>0,定理1得证．

2 平衡点的稳定性

定理2当R0<1时,系统(1)的无病平衡点P0在Ω内是局部渐近稳定的;当R0>1时,无病平衡点P0是不稳定的．

证明系统(1)在无病平衡点P0处的Jacobian矩阵为:

令Φ1(λ)为J(P0)的特征方程,则有

Φ1(λ)=(λ+μ)(λ+φ+μ+θ)·

(4)

解得J(P0)的特征值为λ1=-μ<0,λ2=-(φ+μ+θ)<0,λ3=-(σν+μ+q3)<0和下面方程的根:

λ2+a1λ+a2=0.

(5)

其中,

a1=2μ+η+ε+q2+γ+θ+q1>0,

a2=(η+ε+μ+q2)(γ+μ+θ+q1)-

(η+ε+μ+q2)(γ+μ+θ+q1)(1-R0)．

当R0<1时,a1,a2>0,a1a2>0.根据Hurwitz判据[11],方程(4)的所有根的实部均为负,平衡点P0局部渐近稳定.当R0>1时,a2<0,即方程(4)有根具有正实部,平衡点P0不稳定．

定理3当R0<1时,系统(1)的无病平衡点P0在Ω内是全局渐近稳定的．

证明构造Lyapunov函数

L(t)=ηE+(η+ε+μ+q2)I.

(6)

计算L(t)沿着系统(1)的导数得:

(η+ε+μ+q2)(γ+μ+θ+q1)(R0-1)I,

P0=(V0,E0,I0,Q0,S0)=

根据LaSalle不变集原理[12]可知,当R0<1时,定理3成立．

定理4当R0>1时,地方病平衡点P*在Ω内是局部渐近稳定的．

证明系统(1)在地方病平衡点P*处的Jacobian矩阵为:

J(P*)=

令Φ2(λ)为J(P*)的特征方程,则有

Φ2(λ)=(λ+μ)(λ+φ+μ+θ)·

(λ3+b1λ2+b2λ+b3)=0.

(7)

解得J(P*)的特征值为:λ1=-μ<0,λ2=-(φ+μ+θ)<0和下面方程的根:

λ3+b1λ2+b2λ+b3=0.

(8)

其中,

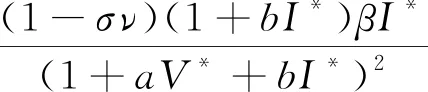
η+ε+q2+γ+θ+q1,

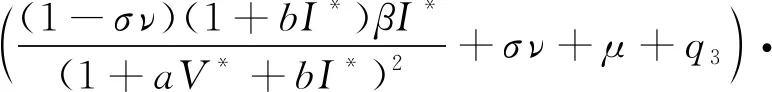
(η+ε+μ+q2)+

(γ+μ+θ+q1)+

(η+ε+μ+q2)(γ+μ+θ+q1)-

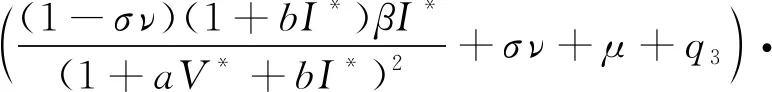
(η+ε+μ+q2)(γ+μ+θ+q1)-

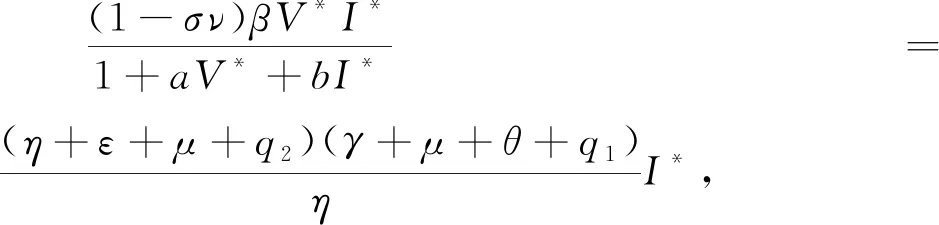
b1,b2,b3>0,Δ1=b1>0,

根据Hurwitz判据[11],R0>1时,方程(7)的所有根都具有负实部,定理4得证．

定理5当R0>1时,地方病平衡点P*在Ω内是全局渐近稳定的．

证明利用Li-Muldowney几何方法[13]来证明.显然系统(1)满足Ω是单连通的且存在一个紧的吸引集K⊂Ω[14].通过上述论证可知,当R0>1时,无病平衡点P0∈∂Ω是不稳定的,而唯一的正平衡点P*∈Ω是局部渐近稳定的.下面仅需证明q<0即可．

首先,考虑系统(1)的子系统

(9)

系统(9)的Jacobian矩阵为

其第二加性复合矩阵为

其中,m=σν+2μ+q3+η+ε+q2,n=σν+2μ+q3+γ+θ+q1,k=η+ε+2μ+q2+γ+θ+q1．

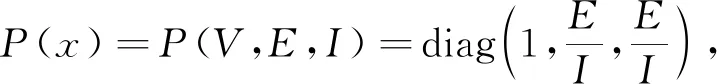
B22=

且

因此可得:

根据文献[4]的定理6,系统(1)的地方病平衡点(V*,E*,I*)是全局渐近稳定的．

现在考虑系统(1)的子系统

(10)

其极限系统为

(11)

然后,根据(11)可得

3 数值模拟和敏感性分析

利用MATLAB验证无病平衡点P0、地方病平衡点P*的稳定性,选择相同的初值(V(0),E(0),I(0),Q(0),S(0))=(50000,25000,25000,0,0)．

图1:取参数Λ=0.82,σ=0.63,ν=0.5,a=0.045,b=0.76,η=0.0082,β=0.046,γ=0.05,φ=0.0005,μ=0.000011,ε=0.0008,θ=0.0013,q1=0.01,q2=0.0023,q3=0.0014.此时R0≈0.8647<1,满足定理3的条件.图1(a)中显示了五种状态的移动设备的数量随时间的变化规律.安全设备S(t)的数量先增加后趋于稳定,隔离设备Q(t)的数量达到峰值后减小,易感设备V(t),潜伏设备E(t)和感染设备I(t)的数量随时间t急剧下降.由图1(b)可知,t趋于无穷时,易感设备V(t)和隔离设备Q(t)的数量达到一个稳定数值,但潜伏设备E(t)和感染设备I(t)为零,意味着病毒传播结束,与定理3的结论一致.

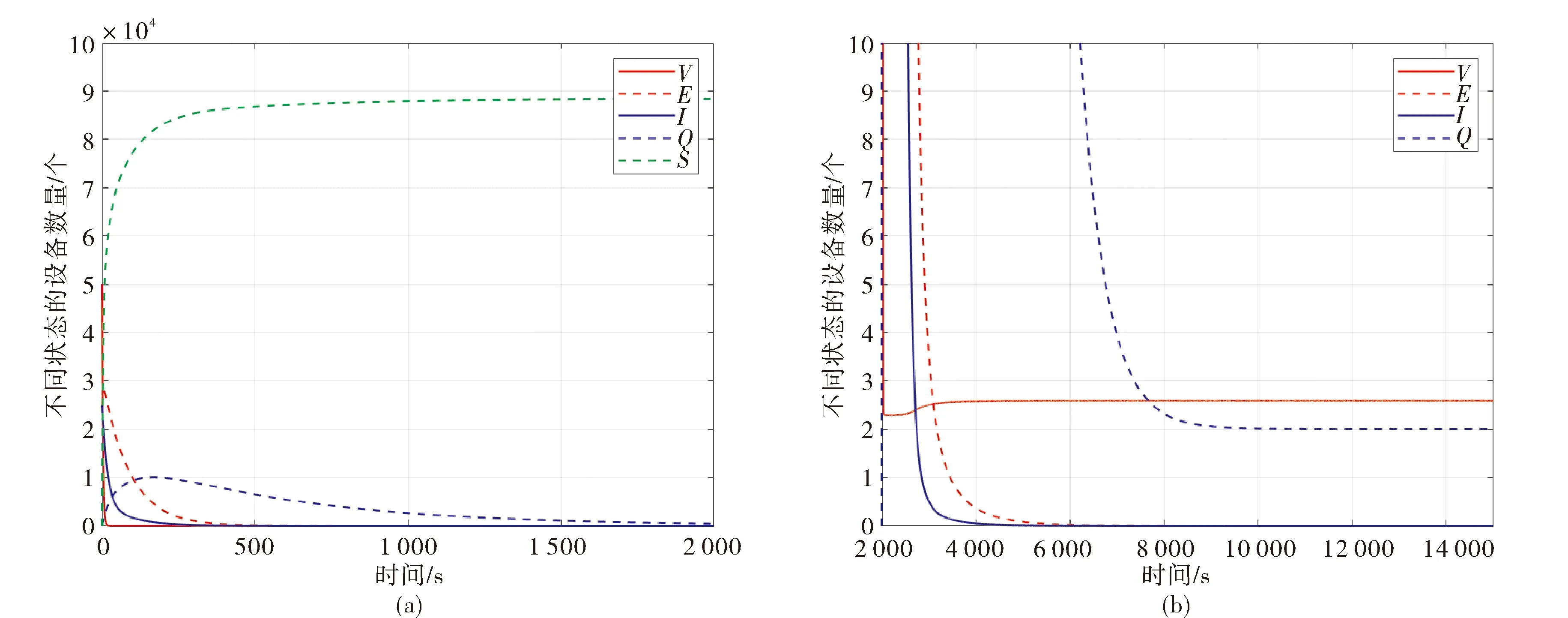
图1 无病平衡点的稳定性Fig.1 Stability of disease-free equilibrium

图2:取参数ν=0.1,其余参数和图1的参数一样.此时R0≈4.1250>1,满足定理5的条件.对比图1(a)和图2(a)知,两图中五种状态的移动设备的数量随时间t变化的总体趋势一致.但当t趋于无穷时,通过图2(b)知道,易感设备V(t),隔离设备Q(t),潜伏设备E(t)和感染设备I(t)的数量都大于零,表明病毒仍然存在,移动设备将持续受到蠕虫病毒的攻击,与定理5的结论吻合．

基本再生数R0和其他参数的关系见图3.其中σ,ν,ε,γ,q1,q2,q3与R0呈负相关,Λ,β,η与R0呈正相关,并且σ,ν,q1的变化对R0更敏感.结果表明,增大感染设备的隔离率q1,增大杀毒软件安装的覆盖率ν及有效率σ都可以使基本再生数R0减小,即减少感染设备与其他设备的连接,以及提高人们对有效抗病毒软件的认识,都可以达到控制蠕虫病毒传播的效果．

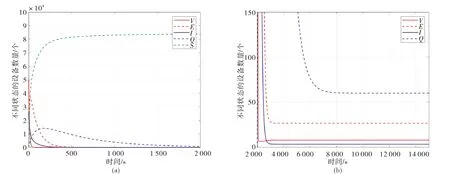
图2 地方病平衡点的稳定性Fig.2 Stability of endemic equilibrium

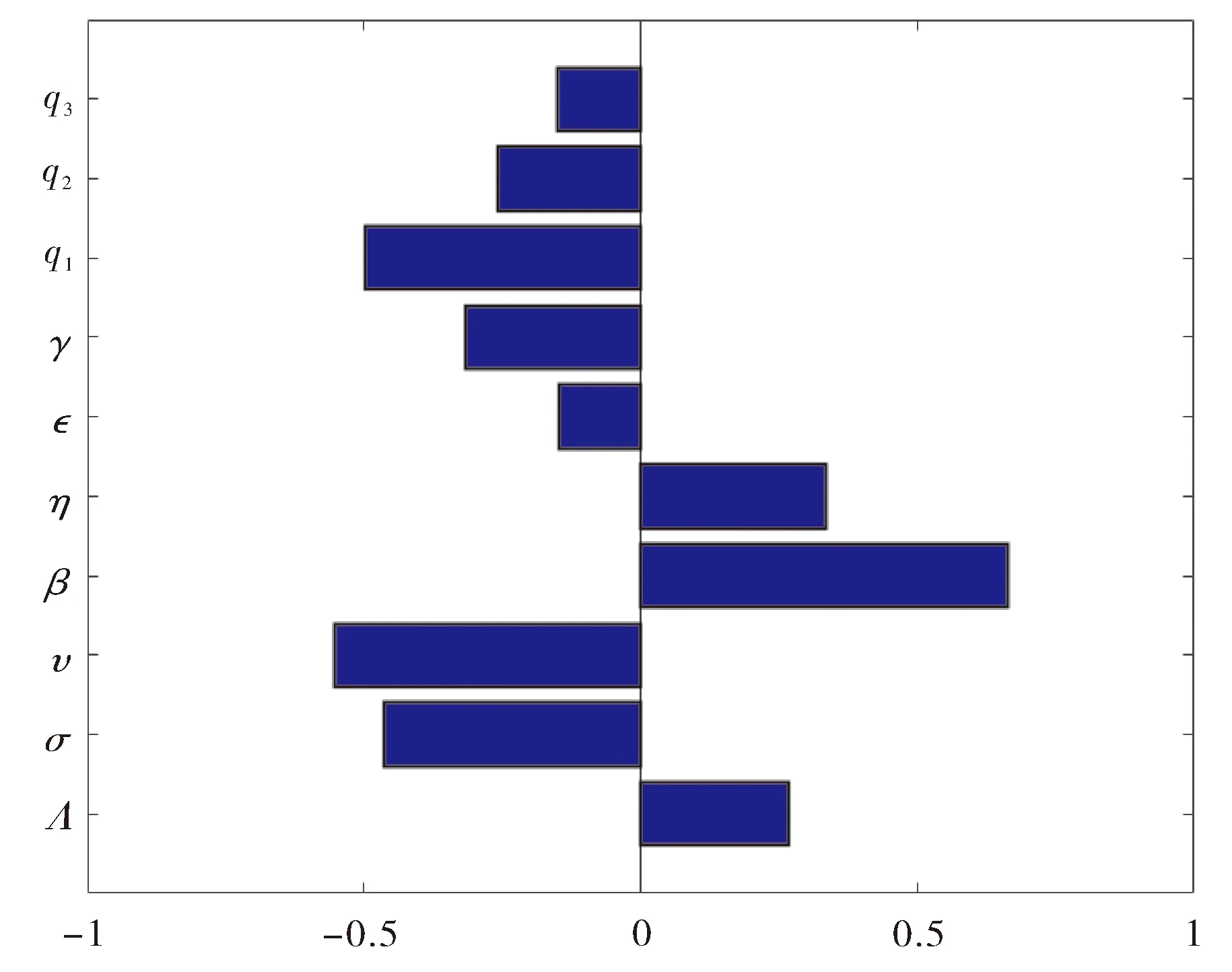
图3 R0与参数的相关性Fig.3 Correlation between R0 and parameters

4 结论

本文讨论了采用疫苗接种和隔离控制策略的具有饱和发病率的网络蠕虫病毒的VEIQS模型的稳定性.通过分析得到以下结论:1)基本再生数R0对蠕虫病毒传播与否起着决定性的作用,当R0<1时,蠕虫病毒传播结束;当R0>1时,蠕虫病毒仍在网络中传播,并通过数值模拟进行了验证.2)移动设备的隔离率以及人们对有效抗病毒软件的认识直接影响着基本再生数R0大小,可以通过加大参数q1,ν和σ的值来减小R0,从而实现对蠕虫病毒传播的控制．