联系抛物Bessel算子的Poisson半群的振荡算子
2023-06-01马毅,陈淼,陈岩,李平
马 毅, 陈 淼, 陈 岩, 李 平
(长江大学信息与数学学院, 湖北 荆州 434023)
近年来, 许多作者研究了调和分析和概率论中与算子半群相关的振荡算子(或变差不等式)[1-7]. Betancor等[8]研究了非局部扩散方程
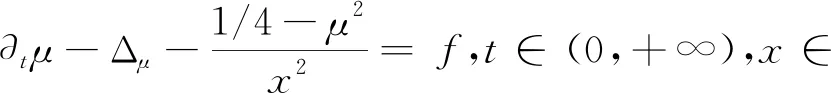
获得了该方程解的加权Lp(2)估计及混合型Lp-Lq估计, 也考虑了抛物Riesz变换. 最近, Li等[7]考虑了联系抛物Hermite算子的Poisson半群的振荡算子, 得到了该振荡算子的Lp有界性.本文主要目的是研究联系抛物Bessel算子的Poisson半群的振荡算子, 利用抛物半群方法和抛物向量值Calderón-Zygmund理论证明了该振荡算子的Lp(2)有界性.当p=∞时, 也考虑了该振荡算子的增长性.
1 预备知识及主要结论
考虑抛物Bessel算子
(1)
其中,Bessel算子Δμ被看作是一维的Schrödinger算子, 其位势
Vμ(x)=-(1/4-μ2)x-2,x∈(0,∞).
Carbonaro等[8]研究了与抛物Schrödinger算子∂t-Δx+V相关的奇异积分.
设hα(x)=(αx)1/2Jμ(αx), 其中Jμ(z)为第一类μ阶Bessel函数.则
Δμhα(x)=α2hα(x),α>0,
即hα(x)是Δμ的特征函数.联系Bessel算子Δμ的热半群{e-τΔμ}τ>0由核的积分给出[9], 事实上, 对于足够好的函数φ,
(2)
其中,
Iμ表示第一类修正的μ阶Bessel函数.对于每一个μ>-1,
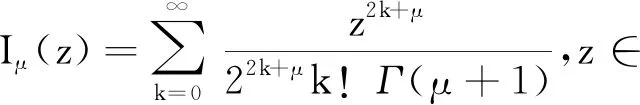
(3)
容易得到, 当λ>0时, 复积分
是绝对收敛的[10], 利用上述复积分, 定义
其中,
e-τ(∂t+Δμ)=e-τ∂t∘e-τΔμ=e-τΔμ∘e-τ∂t.
因此, 对足够好的函数φ, 联系抛物Bessel算子L的热半群为
e-τ(∂t+Δμ)φ(x,t)=e-τΔμφ(x,t-τ)=
类似于经典情况, 利用Bochner从属原理, 联系抛物Besssel算子的Poisson半群e-τ(∂t+Δμ)为
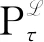
(4)
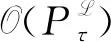
(5)
序列{aj}j∈的一个典型例子是aj=qj(j∈), 其中常数q≥1.
本文的主要结果如下.
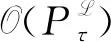
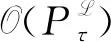
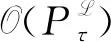
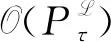
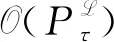

(x,t),(y,s)∈×.
注意到, 在此抛物距离下有
|B((x,t),r)|=|B((0,0),r)|~r3,
其中,B((x,t),r)={(y,s)∈2:|x-y|+ 本文中,C总是表示不依赖于维数和某个函数的正常数, 并且在不同的地方C可能是不同的.本文也经常使用估计式: 对每一个正常数C和非负常数c有 引理1[7]设ξ∈n,ρ∈.则存在一个常数C, 使得 设f(x,t)是定义在n×上的函数, 其Fourier变换定义为 引理2设集合A为 证明因为 那么, 可得 证毕. 然而, 注意到, 当1≤aj+1/aj 因此, 利用Plancherel定理可得 证毕. (6) 因为 所以, (7) 由定理3和(7)式知, 算子T从L2(2)到2)是有界的.下面将证明算子T可以表示为一个奇异积分算子且其向量值核满足所需条件.事实上, 利用Fubini定理, 由(4)式可得 其中, (8) 对向量值核gj, 有下面的估计. 定理4设gj(x,y,s)是(8)式中定义的函数,则 在证明定理4之前, 给出以下引理. 引理3[7]对任意整数N≥1和常数C>0, 设 K(x,t)=t-(n+N)e-|x|2/(ct),x∈n,t∈. 那么 K(x,t)≤C(t1/2+|x|)-2(n+N). 定理4的证明1) 由(8)式可得 因为 所以, 回忆修正的Bessel函数Iμ(z)(μ>-1)的一些性质[8]: (9) Iμ(z)= z∈, (10) 其中,[μ,0]=1, 且 k∈,k≥1, z∈(-∞,0]. (11) 使用(9)~(11)式可得, 当μ>-1/2时, x,y,τ∈(0,∞). (12) 当-1<μ≤-1/2时, (13) 因此, 联立(12)和(13)式可得 2) 由(8)式可得 类似于1)的证明可得 由(1)式可得 因此, 得到 类似地计算可得 因此, 结合上面的计算可得 3) 类似于2)的证明, 得到3)的结论成立.证毕. 定理1的证明由定理3知道算子T从L2(2)到2)是有界的, 结合定理4并使用抛物向量值Calderón-Zygmund理论, 立即得到算子T从Lp(2)到2)是有界的(1 定理2的证明由(8)式和Hölder不等式可得 由定理4 1)的证明可知, 进而, 可得 利用Fubini定理可得 由定理4 1)可得, 所以, 另一方面, 所以, 证毕.2 L2有界性

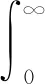
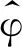
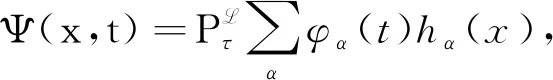

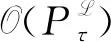

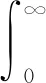
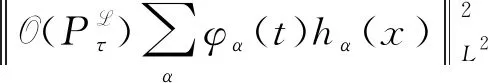

3 核的标准估计
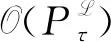
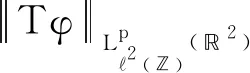
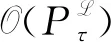
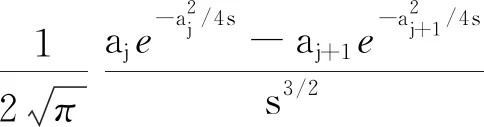
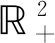
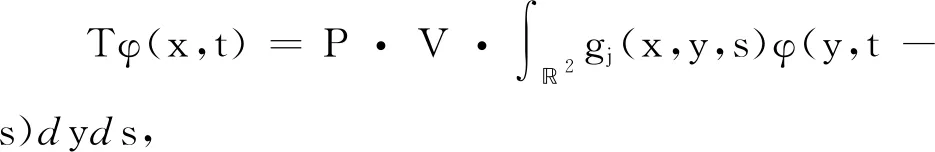
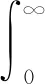
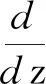
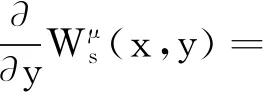
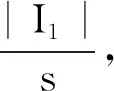
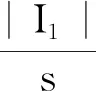
4 振荡算子的增长性

