刚性弹体撞击蜂窝结构高过载特性
2023-05-31魏欣张云峰赵奇峰随亚光张德志张钱城
魏欣, 张云峰, 赵奇峰, 随亚光, 张德志, 张钱城
(1.西北核技术研究所 强脉冲辐射环境模拟与效应全国重点实验室, 陕西 西安 710024;2.西安交通大学 机械结构强度与振动国家重点实验室, 陕西 西安 710049)
0 引言
高过载环境模拟是武器装备、航空航天和轨道交通等领域的重要研究方向之一。特别是在兵工领域,随着高超音速武器、钻地武器等的广泛应用,其关键零部件在高过载环境中的可靠性问题尤为突出,高过载环境模拟成为制约高新武器装备发展的关键技术。围绕高过载环境模拟,国内外学者开展了大量的研究。现有的高过载环境模拟方法主要包括实弹射击法、马歇特锤击法[1-2]、落锤实验法[3-5]、霍普金森杆法[6]和轻气炮加载法[7-10]等,上述方法在经济性、过载波形匹配、适用对象等方面已无法满足现代武器装备研发需求。使用装有关键零部件的刚性弹体撞击金属蜂窝结构可产生特定高过载信号,通过改变弹体撞击速度及蜂窝结构尺寸,可使弹体轴向过载信号连续可调。该方案可能成为一种新的高过载环境模拟技术。
目前,国内外学者对蜂窝结构的动态力学特性进行了一定程度的研究。万峻麟等[11]研究了蜂窝结构轴向低速冲击性能。Yamashita等[12]等通过落锤实验研究了低速加载条件下蜂窝结构的力学性能。研究结果表明,在蜂窝结构胞元尺寸相同的条件下,蜂窝壁厚越大,其峰值压力值越大,正六边形蜂窝结构峰值压力高于正方形蜂窝结构。 Zhao等[13-14]通过霍普金森压杆法研究了动态压缩下蜂窝结构的力学性能。研究结果表明,当冲击速度为2~28 m/s时,正六边形铝蜂窝结构的面外冲击屈服压力比静态条件下提高了40%。Wu等[15]和Baker等[16]是为数不多使用气炮加载方法研究相关问题的学者。Wu发现同一样品在动态实验中的屈服强度比静态下强74%,同时也发现在相同面密度条件下使用整体更小的蜂窝结构可以获得更高的力学性能。Baker发现准静态条件下试样变形为沿着长度方向均匀分布,而动态条件下变形是从冲击端传播的。上述成果主要以蜂窝结构及其动态响应为研究对象,对撞击体的过载特性研究鲜有报道。Zarei等[18]通过落锤实验测得了撞击蜂窝结构过程的加速度-时间历程曲线。但该方法产生的过载波形脉宽太短,无法满足大尺寸武器高过载特性模拟需求。
本文通过刚性弹体高速撞击不锈钢正方形蜂窝结构实验,研究了弹体加速度、速度和位移-时间历程及其变化规律,和蜂窝结构在冲击过程中的力学行为,探索了该技术在应用于高过载模拟领域的可能性。
1 实验试样制备及现场布置
1.1 试样制备
弹体、弹托和弹载存储器的结构如图1所示。弹体主体为一个直径80 mm的圆柱体,为确保弹体对蜂窝结构的面外冲击,避免侵彻作用,弹体前端设计有直径110 mm的圆台。弹体内部为直径60 mm的柱状空腔,用以安放弹载存储器,确保弹载存储器在安放过程中轴向固定。为使弹体在撞击过程中不发生塑性变形,保护内部的弹载存储器,弹体选用强度较高的40Cr钢,也因此可将弹体视为刚性弹体。弹体外包裹有尼龙弹托,可防止划伤炮管,实现弹体次口径发射。
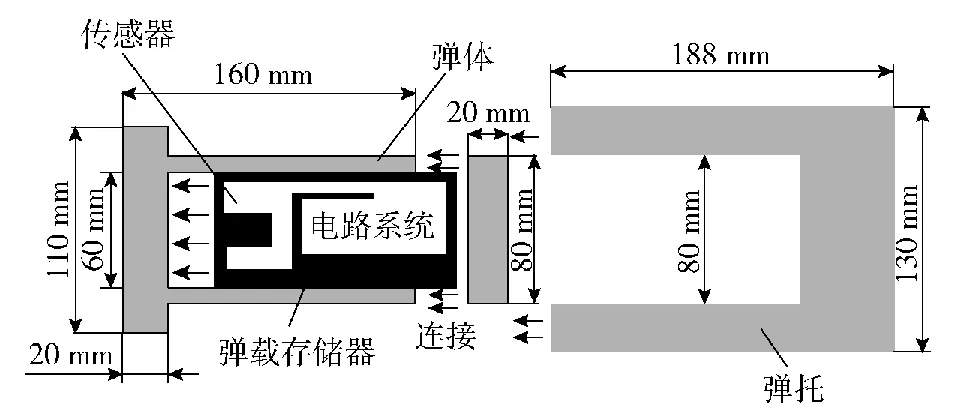
图1 弹体、弹载存储器和弹托示意图Fig.1 Schematic of the projectile, recorder and sabot
弹载存储器由传感器、电路装置和电池组成:传感器为压阻式传感器,用以测量弹体加速度信号,置于弹体前端盖内;电路装置主要功能为存储和逻辑运算;电池为整个弹载存储器提供能源,电路装置和电池置于弹体内部空腔。弹载存储器抗过载能力为1.5×105g(g=10 m/s2),量程为1.2×105g,采样频率为5×105s-1,分辨率为60g。在撞击过程中,传感器测量到的信号为刚体轴向加速度与弹载存储器的谐振频率之和,在后期数据处理过程中需要进行滤波处理。
为减少研究变量,选取正方形蜂窝结构为研究对象。蜂窝结构在西安交通大学机械强度与振动国家重点实验室制备,其尺寸如图2(a)所示,蜂窝结构材料为304不锈钢,单元边长为5 mm,壁厚为 0.3 mm,整体截面尺寸为70 mm×70 mm。为增加弹体撞击蜂窝结构的过载脉宽,采用400 mm长的蜂窝结构进行实验。受制于蜂窝结构的现有制备工艺,单层蜂窝结构的长度均控制在100 mm,制作轴向尺寸较大的蜂窝结构需要采取分段焊接的方式。蜂窝结构的制备过程如图2(b)所示,将带有缺口的金属板条组装,涂抹钎焊浆料(Ni-Cr25-P10)后放入钎焊炉进行钎焊,形成边长100 mm的正方形蜂窝结构;将钎焊好的两段边长100 mm的蜂窝结构再次进行钎焊,形成200 mm长的蜂窝结构;两段 200 mm 长的蜂窝结构通过对接后于外部添加铅块进行氩弧焊接(后文统称铅焊),最终制成400 mm长的蜂窝结构。
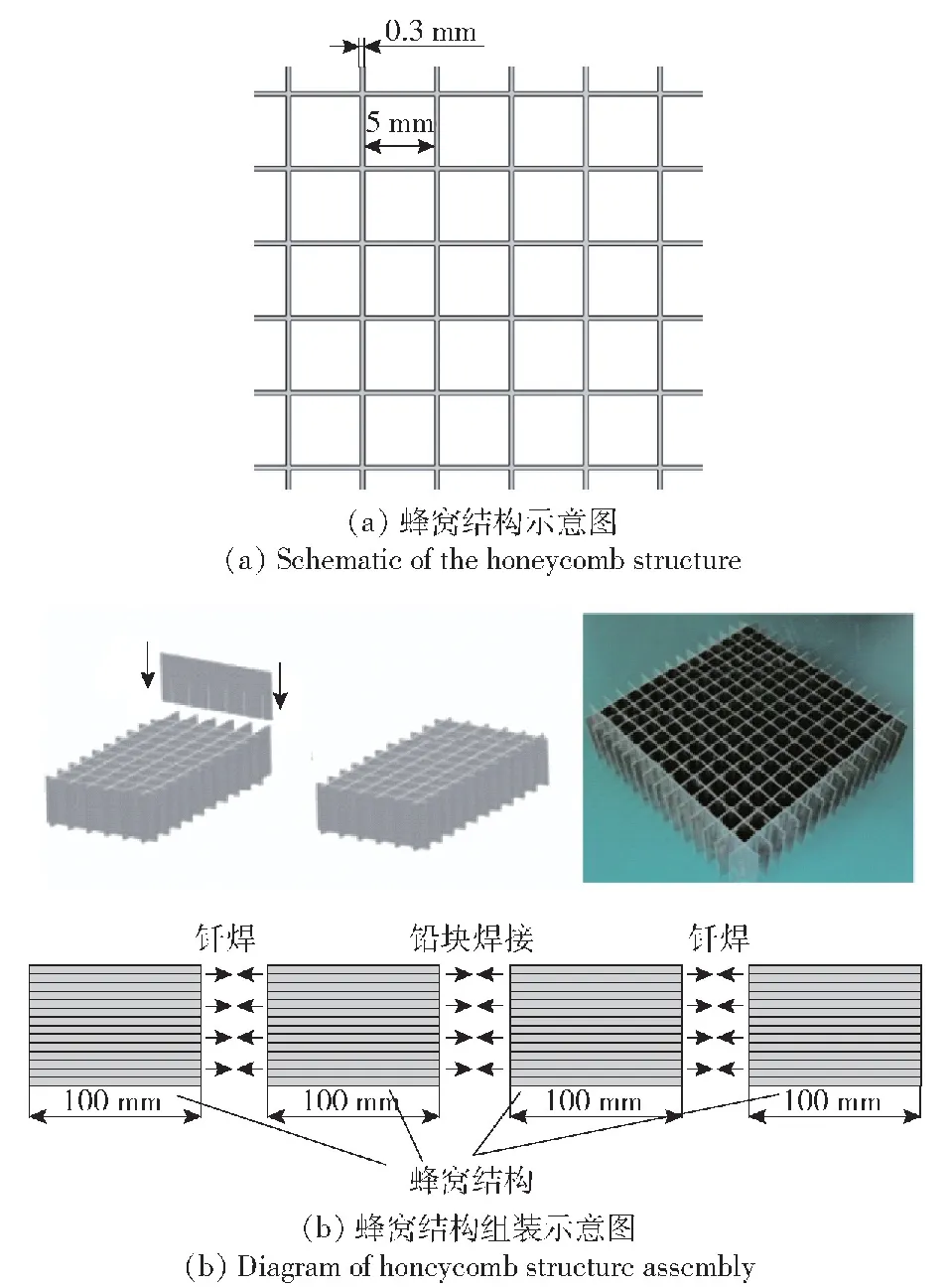
图2 弹体及蜂窝结构示意图Fig.2 Schematic of the projectile and honeycomb structure
1.2 实验布置
实验布置如图3所示,装有弹载存储器的刚性弹体由西北核技术研究所130 mm一级轻气炮发射,撞击固定于大质量块上的蜂窝结构,炮口处以激光遮断法测得弹体出炮口速度近似为撞击速度,通过改变气炮气室压力,可调节弹体撞击速度。图3中,v为弹体撞击速度。蜂窝结构侧面架设高速相机,记录撞击过程中蜂窝结构的变形破坏情况,高速相机以示波器作为触发器,示波器接收到炮口激光遮断信号的同时触发高速相机,高速相机的帧频率设置为2×105s-1。

图3 实验模型Fig.3 Experimental model
实验工况如表1所示,共进行3发实验。以弹体撞击速度为唯一变量,蜂窝结构尺寸保持不变,3发实验的弹体撞击速度分别为182 m/s、218 m/s和246 m/s。表1中弹体质量为弹载存储器、弹体、弹托质量之和,受加工精度的影响,3发实验弹体质量有细微差别。
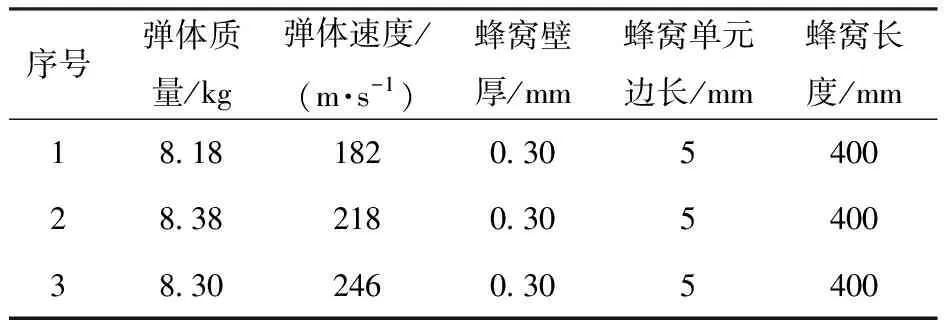
表1 实验工况
2 实验结果分析
2.1 蜂窝结构冲击压缩过程
图4为第1发实验中蜂窝结构的冲击压缩过程。为分析方便,将撞靶时刻定义为0 ms时刻。图4(a)为t=0.45 ms时刻,此时蜂窝结构第1段已近乎压溃,第3、4段钎焊处出现明显的破坏。图4(b)为t=0.95 ms时刻,蜂窝结构第2段已接近完全破坏,但第2、3段连接处依然较完整,表明铅焊工艺强度较高。图4(c)为t=1.30 ms时刻,蜂窝结构第2段已完全被压溃,第3、4段连接处也出现明显的压溃现象。图4(d)为t=2.65 ms时刻,此时蜂窝结构完全被压溃。

图4 第1发实验蜂窝结构冲击压缩过程(v=182 m/s)Fig.4 Impact compression process of the honeycomb structure in the first experiment (v=182 m/s)
图5为第2发实验中蜂窝结构的冲击压缩过程。图5(a)为t=0.35 ms时刻,此时蜂窝结构前端与第1、2段钎焊处已出现压溃现象。图5(b)为t=0.80 ms时刻,可以看到蜂窝结构第2、3段铅焊处发生弯折,表明该组实验的铅焊处的结构强度较弱,铅焊工艺的稳定性较差。图5(c)为t=1.25 ms时刻,可以看到蜂窝结构第3段发生整体弯折,由于整体弯折的吸能作用,在弹体到达前第3、4段钎焊处并未出现压溃现象。图5(d)为t=2.20 ms时刻,蜂窝结构被整体压溃。

图5 第2发实验蜂窝结构冲击压缩过程(v=218 m/s)Fig.5 Impact compression process of the honeycomb structure in the second experiment (v=218 m/s)
图6为第3发实验中蜂窝结构的冲击压缩过程。图6(a)为t=0.25 ms时刻,此时蜂窝结构前端与第1、2段钎焊处已出现压溃现象。图6(b)为t=0.65 ms时刻,此时蜂窝结构前端与第1、2段钎焊处已出现压溃现象。图6(c)为t=1.00 ms时刻,蜂窝结构第1、2段已完全压溃,第3、4段钎焊处出现明显的压溃现象,且第3、4段间出现错位。图6(d)为t=2.00 ms时刻,蜂窝结构被整体压溃。第3发实验蜂窝结构冲击压缩过程与第1发实验相似,压溃现象发生次序为蜂窝结构前端,1、2段钎焊处和3、4段钎焊处,而2、3段铅焊较为牢固,在弹体到达前未发生压溃。对比3发实验结果,第2发实验铅焊强度低,导致蜂窝结构第3段整体弯折,应属加工工艺不成熟导致的偶然现象;第1、3发实验的蜂窝结构的冲击压缩过程为加工工艺合格时的典型实验现象。

图6 第3发实验蜂窝结构冲击压缩过程Fig.6 Impact compression process of the honeycomb structure in the third experiment (v=246 m/s)
2.2 刚性弹体加速度响应规律
图7~图10为第1发实验弹载存储器测得的全弹道加速度历程。从t=0 ms时刻开始,加速度曲线比较平缓,随后有一段小幅震荡,峰值在1 000g以内,再进入大幅震荡。从小幅震荡到大幅震荡之间共经历了6.23 ms,假设小幅震荡为弹体撞击塑料薄膜时的过载,弹体撞击速度为182 m/s,算得该段时间弹体移动距离为1.13 m,而炮口距蜂窝结构顶端1.12 m,可判定前端小幅震荡曲线为弹体撞击炮口塑料薄膜时的加速度曲线,而大幅震荡曲线起始时刻即为撞靶时刻,这一结论在剩余2发的数据中也得到了验证。曲线大幅震荡后出现持续的减加速度,减加速度未归零,与实际情况不符,判断蜂窝结构完全压缩后,弹体撞击密实蜂窝结构,导致弹载存储器损坏,数据失真。通过高速摄影图像可判断弹体冲击压缩蜂窝结构的持续时间,后续研究仅截取从弹体撞靶时刻到蜂窝结构完全压缩时刻的实验数据。
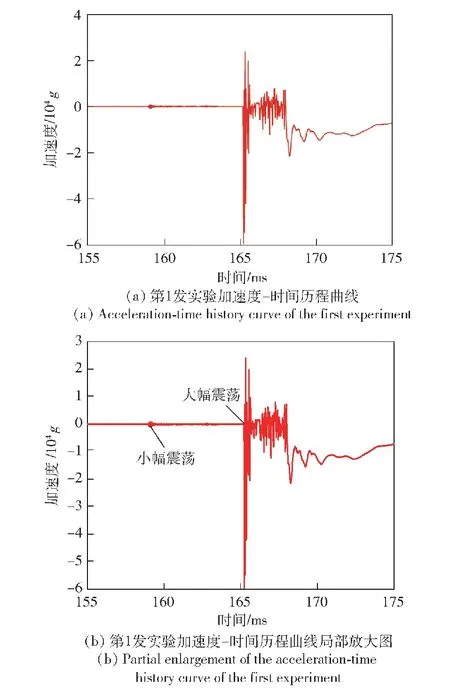
图7 第1发实验加速度曲线Fig.7 Acceleration curve of the first experiment
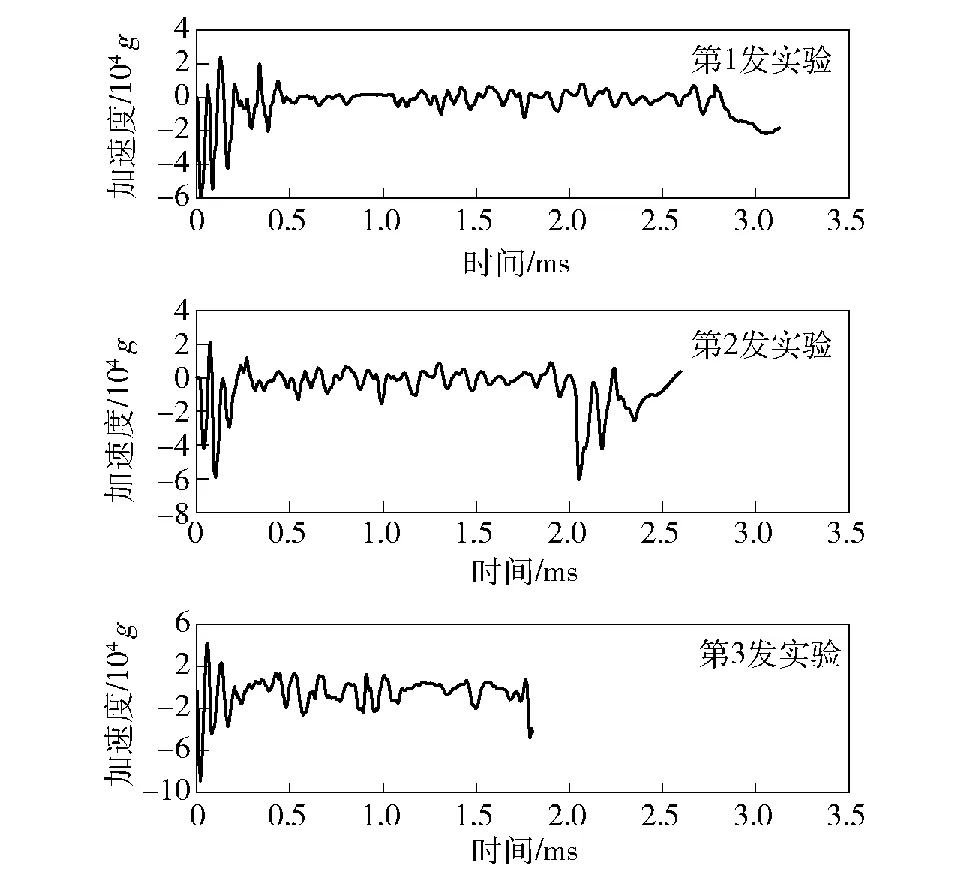
图8 3种工况下的加速度-时间历程曲线Fig.8 Acceleration-time history curves of the three conditions
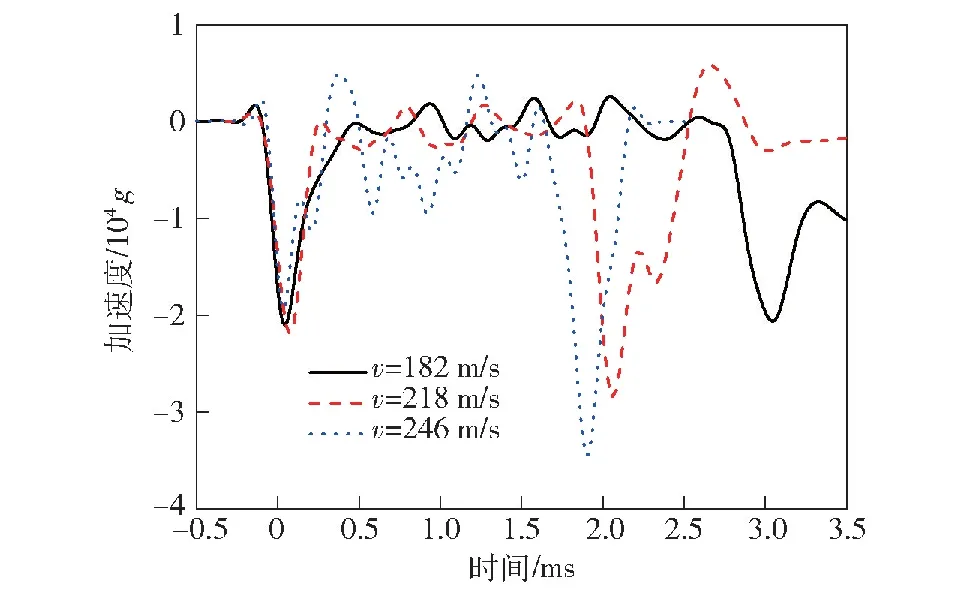
图9 3种工况下的滤波加速度-时间历程曲线Fig.9 Acceleration-time history curves after filtering of the three conditions
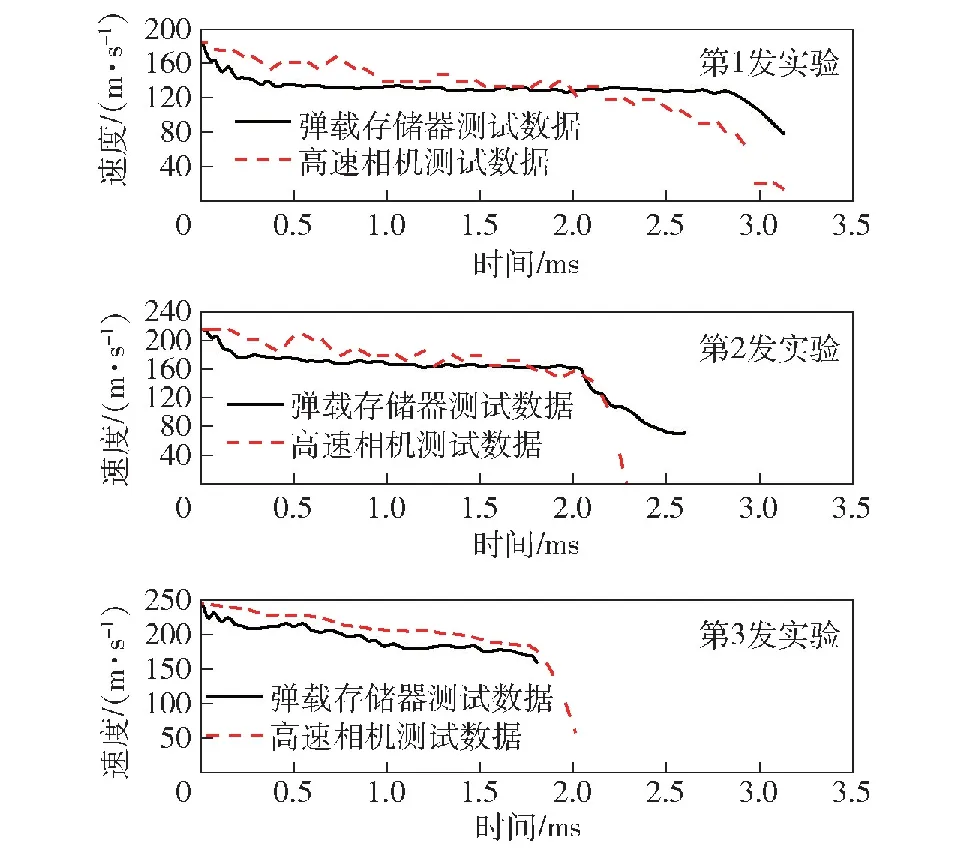
图10 3种工况下的速度-时间历程曲线Fig.10 Velocity-time history curves of the three conditions
图8为3发实验的弹体加速度曲线。结合高速摄影图像,可将弹体对蜂窝结构的冲击压缩分为 3个阶段:阶段1为弹体撞击蜂窝结构瞬间及其后的加速度曲线高幅震荡阶段,可称为初始冲击阶段,对应蜂窝结构处于弹性阶段,未进入塑性变形;阶段2为加速度曲线维持低幅震荡阶段,可称为稳态压缩阶段,对应蜂窝结构进入塑性与弯折变形,对弹体的阻力减小;阶段3为弹体加速度曲线震荡幅值再次陡然升高,可称为密实压缩阶段,对应蜂窝结构被压缩密实,弹体阻力陡然增加,由于后期传感器损坏,无法准确判断出此阶段的持续时间。
按照参考文献[18]中的方法,对弹载存储器测试得到的加速度-时间历程曲线进行频谱分析,选取5 kHz作为截止频率进行滤波,消除弹载存储器前端盖的谐振带来的影响。图9为弹体轴向刚性加速度-时间历程。由图9可以看出:3发实验的弹体在初始冲击阶段的过载峰值相差不大,3发分别为-2.10×104g、-2.19×104g、-1.93×104g;进入稳态压缩区后,第1、2发实验震荡幅度相当,第3发实验的震荡幅度较大;稳态区持续时间随撞击速度的增加而减小。3发实验的稳态时间分别为2.28 ms、1.65 ms和1.25 ms;密实区过载峰值随撞击速度增加而增加,3发实验的密实区过载峰值分别为 -2.06×104g、-2.80×104g和-3.45×104g。
Xu等[19]和Wang等[20]分别通过实验结果和理论分析发现了蜂窝结构动态平台强度与静态平台强度的关系。在以上强度理论的基础上,结合本文实验工况,预测加速度峰值amax如下:
(1)
(2)
(3)
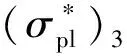
由表2可见,3发实验与理论预测的偏差均在10%以内,结果表明,理论公式可以准确预测实验结果。从式(1)、式(2)、式(3)中可以看出,加速度峰值的大小是由蜂窝结构自身坍塌强度和弹体质量决定的:通过改变弹体撞击速度和蜂窝结构厚跨比,可以改变蜂窝结构的应变率强化效应和等效密度,以达到改变蜂窝结构对弹体的阻力;通过改变弹体质量可以改变相同阻力下的加速度;通过以上方法可以改变蜂窝结构的过载峰值。

表2 实验与理论预测的加速度峰值对比
2.3 刚性弹体速度响应规律
图10为弹载存储器与高速相机获得的弹体速度曲线,弹载存储器测得的速度曲线为加速度曲线积分所得,高速相机测得的速度曲线为位移曲线微分所得。与加速度曲线对应,速度曲线在3个阶段也有不同的响应特征:初始冲击阶段速度曲线快速下降,对应弹体撞击蜂窝结构后加速度曲线大幅震荡;稳态压缩阶段速度曲线缓慢下降,对应加速度曲线小幅震荡;密实压缩阶段速度曲线再次快速下降,对应蜂窝结构被压缩密实后,弹体阻力增大导致的加速度陡然增大。稳态压缩阶段,第3发实验的速度曲线斜率明显大于前两发,对应第3发实验的加速度曲线振幅更大,即蜂窝结构对弹体的阻力具有应变率相关性,该阻力随应变率增大而增大。曲线后半段,弹载存储器损坏,以高速相机图像处理结果为准。
从图10中可以看出,初始冲击阶段速度曲线呈现阶梯状下降形态。假设应力波在弹体中大概以弹性杆波速c传播:
(4)
式中:E为弹体弹性模量,E=206 GPa;ρ为弹体密度,ρ=7.5 g/cm3。由式(4)算得c=5 240 m/s。第1发实验速度曲线初始冲击阶段每个阶梯的周期约为0.073 ms,周期内应力波传播距离为382 mm,约为2倍弹体长度,进一步验证了测试结果的准确性。
弹体撞击蜂窝结构后,产生向弹体自由端传播的压缩波,压缩波到达弹体自由端后,产生向弹体头部传播的卸载波,随着卸载波到达弹体头部,弹体完成一个减速周期,明显地,速度曲线的阶梯状下降为应力波在弹体中周期性传播导致。从第2发、第3发实验曲线中也可得出相同的结论。
在蜂窝结构吸能特性的研究中,总吸能量Ebd可表示为
(5)
(6)
式中:Ebd为动态条件下蜂窝结构的总吸能;d为进入密实区时,蜂窝结构的压缩量;F(s)为弹体撞击蜂窝结构的阻力;v0为弹体撞击速度;v1为进入密实区时刻弹体速度;am为弹体进入密实区前的平均加速度;Fm为弹体平均阻力。如表3所示,3发实验动态条件下蜂窝结构进入密实区前的总吸能水平和平均加速度明显上升。

表3 3发实验的总吸能量和平均加速度
王中刚[21]在其研究成果中提出,动态总吸能量Ebd可表示为蜂窝结构静态理论吸能量与动态吸能量的相加形式:
(7)
式中:Eb为蜂窝结构的静态理论吸能量;D和P为动态本构模型的材料参数;C(μ)为修正系数项,反映了不同厚跨比蜂窝结构在不同加载率下的结构力学特性,与厚跨比μ密切相关。
从实验结果中可以看出,蜂窝结构总吸能量与弹体撞击速度密切相关,3发不同撞击速度的弹体所引起的动态吸能量的变化效果显著。由此可见,加载速率对蜂窝结构进入密实区前的总吸能量和平均加速度影响较大。
2.4 刚性弹体位移响应规律
图11为弹载存储器与高速相机获得的弹体位移曲线,弹载存储器得到的位移曲线为加速度经过二次积分得到的结果。由于初始冲击阶段和密实压缩阶段持续时间较短,而稳态压缩阶段速度变化较小,因此弹体位移曲线接近直线。依据实践经验,弹载存储器测得的位移曲线误差为10%左右[18]。其误差主要来自于:传感器自身的测试误差;加速度数据二次积分的累积误差;数据处理时起始点选择引起的误差;弹体冲击过程中内部结构微小变化引起的误差等。因此,一般可以认为采用高速相机图像处理获得的位移曲线较弹载存储器测试结果精确。
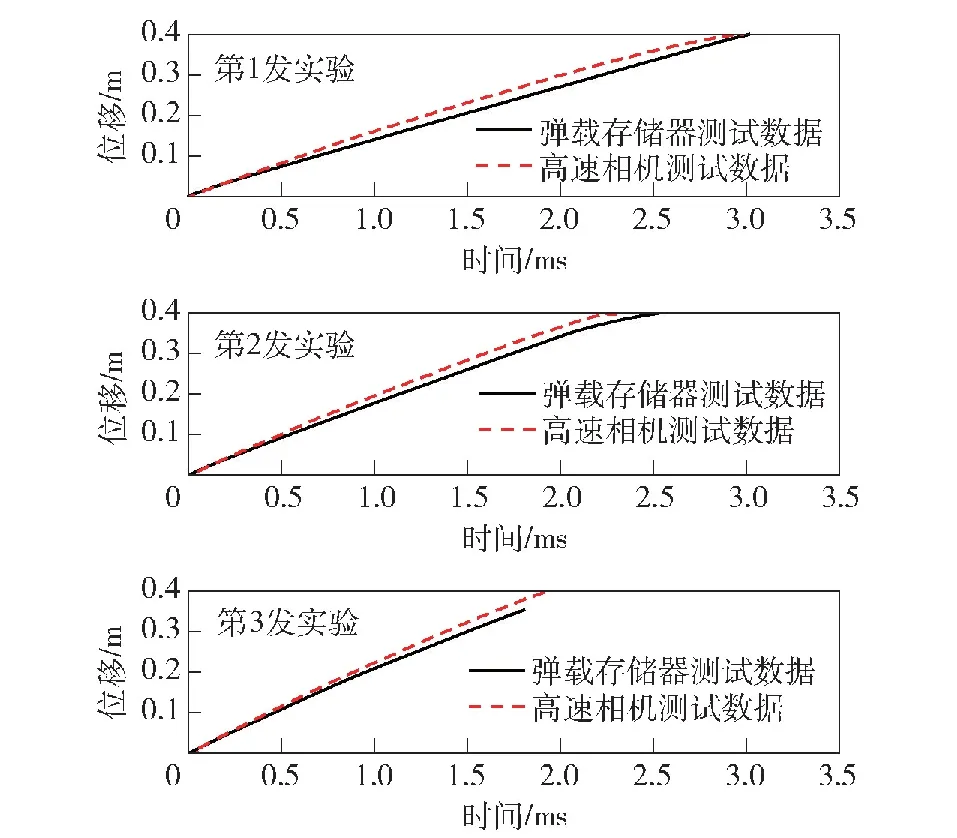
图11 3种工况下的位移时间历程曲线Fig.11 Displacement-time history curves of the three conditions
3 结论
本文通过刚性弹体高速撞击不锈钢正方形蜂窝结构实验,研究了弹体加速度-时间、速度-时间和位移-时间历程及其变化规律,以及蜂窝结构在冲击过程中的力学行为。得出以下主要结论:
1)刚性弹体高速撞击造成的蜂窝结构压溃是高度局部化的力学行为,压溃首先发生在蜂窝结构顶端,并随弹体运动由顶端向底端传播。该过程中,蜂窝结构脆弱处(如钎焊处)进而发生破坏压溃现象,并导致蜂窝结构整体失稳、错位。
2)弹体对蜂窝结构冲击压缩过程可分为初始冲击、稳态压缩、密实压缩3个阶段,加速度曲线分别呈现大幅震荡、小幅震荡、再次大幅震荡的形态,分别对应弹体对蜂窝结构的初始撞击压缩、蜂窝结构压溃失稳、蜂窝结构被压缩密实阻力增加3个过程。
3)通过预测公式,可以较为准确地预测弹体高速撞击蜂窝结构的加速度峰值,并详细分析了加速度峰值的影响因素。
4)刚性弹体的速度曲线呈先快速下降、而后缓慢下降、再快速下降的形态,与加速度曲线相对应。初始冲击阶段的速度曲线呈明显的阶梯状下降形态,为应力波在弹体中周期性传播导致,且第1个周期内,弹体内应力波幅值呈随弹体撞击速度增大而增大的趋势。
5)通过对实验中蜂窝结构吸能量及平均加速度的计算发现,加载速率的变化对蜂窝结构的吸能量和平均加速度的影响较为显著。
