基于QAR数据的飞行环境风建模方法

刘家学,陈田君宏,郭润夏,钱文高

(中国民航大学 电子信息与自动化学院, 天津 300300)

0 引言

风对飞机的飞行状态有着巨大影响,是飞行仿真的重要组成部分[1]。建立一种适用于飞行仿真的环境风模型,从而研究飞行器在风扰动下的响应状态是当前飞行仿真研究中的重要内容[2]。

肖叶伦等[3]建立了以平均风,阵风、紊流3个分量为基础的环境风模型。由于阵风和紊流都表征风的脉动特性,所以范大蔚和佟佳慧[4]基于随机波浪理论建立了以平均风和脉动紊流为基础的两分量环境风模型。

上述2种环境风模型中的紊流分量都是由功率谱进行描述。常用的紊流功率谱有Von Kaman谱、Dryden谱以及Davenport谱等。屈香菊和李勇[5]基于Von Kaman谱对Dryden谱进行了改进,解决了Dryden谱与实际紊流功率谱在高频区差距较大的问题;吉洪蕾等[6]采用多项式拟合的方法将Von Kaman谱有理化,解决了基于Von Kaman谱的紊流成型滤波器难以设计的问题;肖春生等[7]将多用于建筑风扰分析的Davenport谱应用在飞行环境风仿真中,验证了基于Davenport谱进行飞行环境风仿真的可行性。由于实际大气环境中发生的紊流多数为非Kolmogorov紊流,而Dryden谱、Von Kaman谱和Davenport谱都无法描述非Kolmogorov紊流的能量分布特性[8],为此应对现有紊流功率谱进行适当扩展。

以上研究主要聚焦于风速建模,缺少对风向的考虑。辛欣瑶等[9],季亮等[10]提出了基于马尔可夫过程的风向建模方法,该方法能较好描述风向随时间的变化特性,但对风向和风速的相关性考虑较少。

快速访问记录器(quick access recorder,QAR)在线记录了飞机运行中大量原始数据[11],其中包含飞行过程中的环境信息,本文中基于QAR数据提取环境风特征,建立了可描述非Kolmogorov紊流能量分布特性和风向变化特征的环境风模型。

1 风速仿真模型

1.1 风速模型

飞行过程中的环境风可以看作是平均风和紊流2个分量的叠加[7],其表达式为:

vω(t)=vm(t)+vt(t)

(1)

式中:vω(t)为总风速;vm(t)、vt(t)分别为平均风分量和紊流分量。

1.2 平均风模型

在航空气象学中,平均风通常由固定高度2 min内测得风速的平均值表示。平均风沿高度的分布规律称为风廓线。根据热成风原理,由于高空中大气不受地面摩擦力影响,所以风主要由该高度平面内的气压梯度驱动。当两地地表气温不同时,温度较低一地的气压沿高度方向下降速度更快,随着高度增加,两地在同一高度平面内的气压梯度逐渐增大,导致风速也随高度增加而增大,故不同高度下的平均风速可表示为:

vm=kh+b

(2)

式中:k为风速随高度增加的风廓线系数;h为飞机所在高度与参考平面之间的高度差,单位为英尺;b为参考平面的风速,单位为节。

同样根据热成风理论,风廓线系数与地区间温度差相关。而地区间的温度差会随着季节变化而变化,所以应根据实际记录数据提取不同季节的分廓线系数k。

本文中使用2012年11月至2013年8月自广州白云机场飞往北京首都国际机场航班记录的QAR数据作为实验数据集。表1为基于实验数据集提取的风廓线系数k月分布区间。

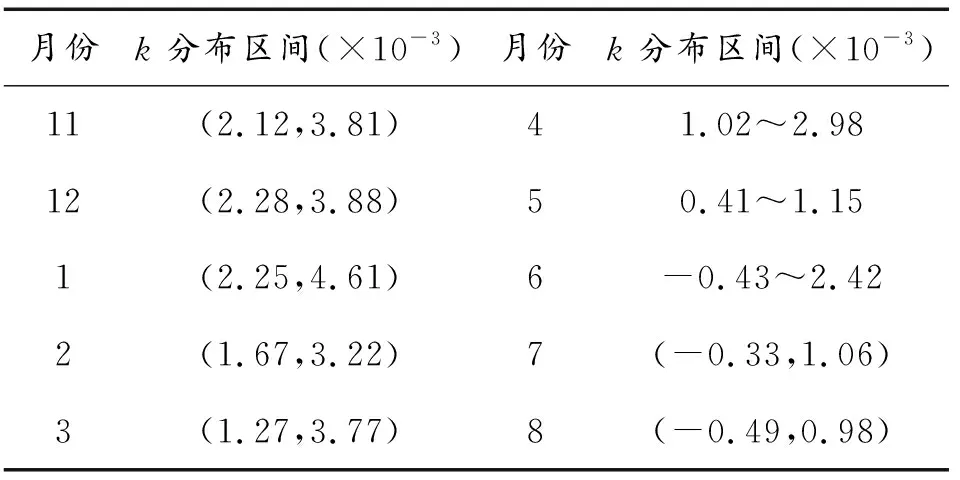
表1 风廓线系数k的月分布区间

由表1可见,随着季节改变,月度风廓线系数分布区间有明显差别。冬季风廓线系数明显大于夏季风廓线系数,在11月之后随着南北温差逐月增加,风廓线系数呈逐月递增的趋势,而在3月后,随着南北温差逐月减小,风廓线系数呈逐月下降的趋势,该结果与热成风理论相符。

1.3 紊流模型

紊流vt(t)一般由紊流功率谱描述,基于Kolmogorov理论的紊流功率谱表达式为[12]:

(3)

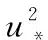
本文中将以Davenport谱作为标准谱进行比较, Davenport谱表达式[4]为:

(4)

式中:C为粗糙系数,最大取值为0.003。

文献[13]中指出并不是所有紊流都满足Kolmogorov假设,即γ-αβ=-2/3。本文中基于QAR记录数据拟合功率谱幂指数λ,λ=γ-αβ,对应的功率密度形式为。

(5)

图1给出了3组紊流实测功率谱曲线与拟合谱曲线,并与Davenport谱进行了对比。图1(a)中拟合谱的拟合参数λ=-1.13,该数值为所有拟合结果中的最大值。图1(b)中拟合谱的拟合参数λ=-1.667。图1(c)中拟合谱的拟合参数λ=-1.98,其为所有拟合结果中的最小值。

由图1可见,只有图1(b)中的实测功率谱在惯性子区间内斜率较好地符合Davenport谱,图1(a),图1(c)都与Davenport谱有一定差距。故根据实测数据的拟合结果,给出λ的取值范围为(-1.98,-1.13)。

图1 实测功率谱与拟合功率谱

2 基于马尔可夫过程的风向建模方法

根据地转风理论,当我国南北温差较大时,自由大气中应盛行西风。图2为基于QAR数据统计所得的不同平均风速下,自由大气中主导风向分布图。

图2 不同平均风速下的主导风向分布

当平均风速小于30节时,主导风向分布范围为(100°,275°),样本较为分散,但当风速大于30节后,风向分布逐渐集中,分布区间缩小为(220°,285°),且72%的样本集中在260°±10°内,该主导风向分布区间符合北半球高空应盛行西风的地转风理论。因此,主导风向为:

(6)

式中:Wd为主导风向;rand()为随机数;MOD为取余运算;N为一次飞行的样本长度。

虽然以上分析确定了不同风速下的主导风向分布情况,但是在飞行过程中,风向是随时间变化的。为了研究风向随时间的变化规律,对风向数据进行一阶前向差分,获得风向在单位时间内的变化情况,如图3所示。

图3 不同风速下的风向变化程度

由图3可见,随着风速增大,单位时间内风向变化逐渐减小。风速在20节以下时,风向振荡较大,最大振荡为每秒12°,风速超过20节时,风向振荡频次和幅度都有明显降低趋势,而风速超过60节时,风向的最大振荡减小为每秒1°。这是因为随着风速增大,风所包含的动能增加,在同等强度的干扰下风向变化越小。为此可以根据风速大小对风向变化进行分段建模,分别研究风速在20节以下、20～60节、以及60节以上时,风向的变化特征。

根据以上对于风向变化的分析并结合文献[9-10]中提出的基于马尔科夫过程进行风向建模和预测的思想,本文中提出基于马尔科夫过程描述风向变化状态的建模方法。由于风向变化与风速相关,所以需要建立不同风速下的状态转移矩阵为:

(7)

式中,P1、P2、P3分别代表风速在20节以下、20节到60节之间以及60节以上时,风向变化的状态转移矩阵。

以P3为例说明如何构建风向变化状态转移矩阵,选取某航班QAR数据中,风速大于60节的风向变化数据进行统计,并将统计结果记录在表2中。

表2 风向变化状态出现频次

由表2可见。该段样本中风向变化共有3种状态:左偏1°、保持当前状态和右偏1°。将左偏1°记录为状态1,右偏1°记录为状态-1,保持当前状态记录为状态0,其数学描述为X={x1,x0,x-1}。根据马尔可夫过程的思想,当前时刻的状态只与前一时刻状态有关,故通过统计当前时刻的状态xi到下一时刻的状态xj的转移频次在当前状态为xi的总转移频次中占比即可获得转移概率Pij。根据表2可写出当前样本下的风向状态转移概率矩阵P3:

(8)

同理可得P2的状态空间为X={x1,x0,x-1,x-2}:

(9)

P1为21维状态转移矩阵,由于版面原因不再列出。

3 仿真实验

3.1 谱幂律范围验证

用2012年1月至9月间航班记录风速数据作为测试集。拟合测试集实测紊流数据的功率谱指数λ,λ频数分布如图4所示。

图4 谱幂率参数分布直方图

图4可见λ的取值多集中于-5/3附近。且测试集中-1.98<λ<-1.13的频数为93.2%,这表明本文中给出的λ取值区间能覆盖大部分实际发生的紊流功率谱。

3.2 风速仿真实验

风速仿真包括平均风仿真和紊流仿真2个模块,平均风仿真可根据仿真月度,依据表1给出的风廓线区间,选择当次仿真使用的风廓线系数k。之后根据式(1)进行平均风仿真。

紊流仿真参考文献[14-15]中提出的方法:将紊流看作白噪声通过成型滤波器后得到的色噪声。仿真步骤如下:

1) 依据紊流功率谱设计成型滤波器。

2) 生成均值为0的白噪声。

3) 将白噪声通过成型滤波器后获得色噪声。

根据以上方法进行冬夏两季的风速仿真实验,对比仿真风速和实测风速的时序序列和紊流功率谱,如图5所示。

由图5(a)和图5(c)可见,虽然仿真风速与记录风速的时序序列并不完全相同,但是仿真风速与实测风速中的平均风在不同季节随高度变化的趋势相同,这说明本文中提出的环境风模型能够反映风廓线随季节变化的特性。

对比图5(b)和图5(d)可见,仿真紊流功率谱与实测紊流功率谱吻合较好,图5(d)中的仿真紊流功率谱和Davenport谱有明显差距,这说明Davenport谱只能描述一部分紊流能量分布,具有一定的局限性。而本文中提出的紊流模型能够描述大部分实际发生的紊流,实现了对Davenport谱的扩展。

3.3 风向仿真实验

图6是风速在20节以下和60节以上时,基于风向模型得到的风向仿真曲线和实测数据的对比结果。

由图6(a)和图6(b)可见,仿真风向曲线和实测数据记录的风向曲线较为相似。分别计算仿真结果和实测样本的统计特征,图6(a)中风向仿真结果的均值为277.1°、方差为88.61;实测样本的均值为269.2°,方差为79.6。图6(b)中仿真结果的均值为209.5°、方差为248.6,实测数据的均值为210.4°、方差为197.7。对比两组数据的统计特征可见,仿真结果的均值误差和方差误差都在合理范围内,因此可说明仿真结果和实测结果有良好的相似性,同时20节以下风向仿真结果的方差明显大于60节以上风向仿真结果的方差,体现出了风向振荡程度随风速增加而减小的特性。

图5 不同季节的风速仿真

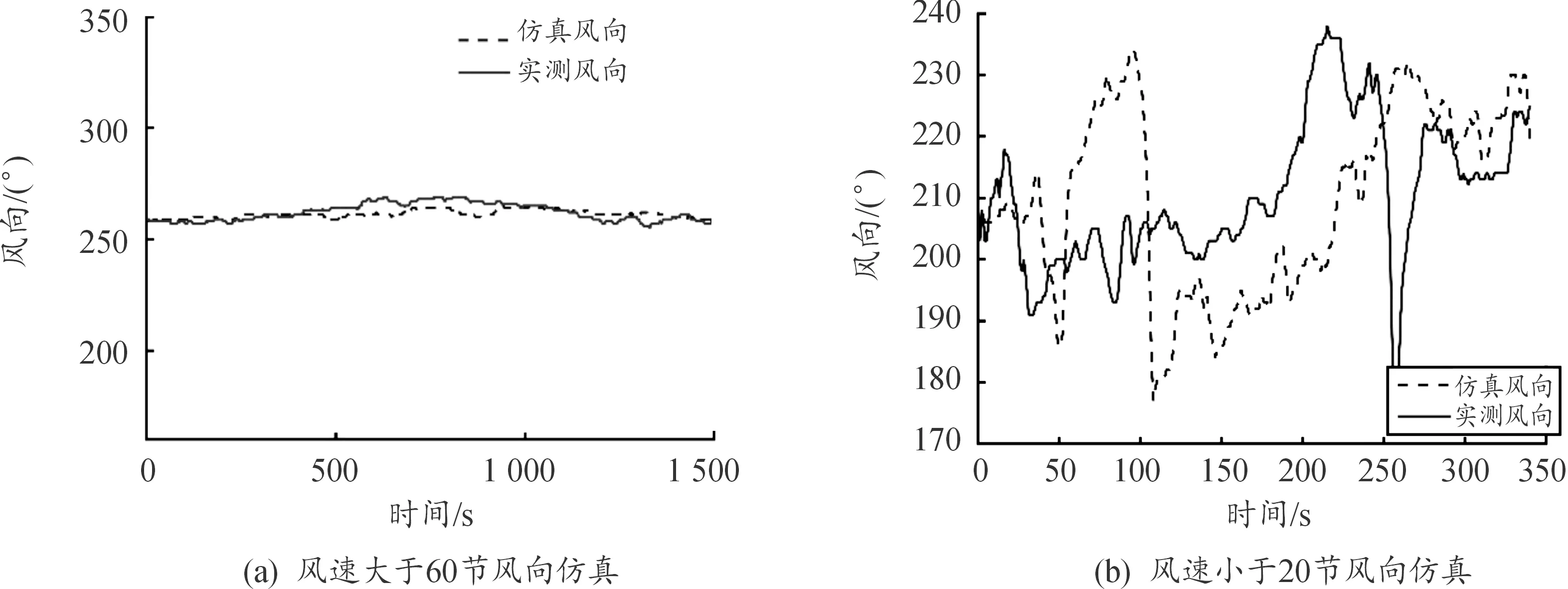
图6 风向仿真结果

3.4 飞行仿真实验

将环境风模型引入实验室自研的飞行仿真平台中进行仿真实验。实验条件为初始时飞机在5 000英尺高度以250节空速进行定常平飞,之后空速逐渐减小至200节。实验组环境风采用图5(a)、图5(c)给出的仿真风场。对照组无风扰输入。除环境风之外,3组实验其他变量均相同。实验结果如图7所示。

图7(a)为空速仿真结果,图7(b)为发动机低压转子N1仿真结果,图7(c)为俯仰角仿真结果。由图可见,在无环境风输入时,空速、N1、俯仰角仿真曲线都平滑无振荡,该结果与实际飞行中的空速、N1和俯仰角变化规律不相符。

对于空速来说,空速是风速和地速的矢量和,其受风速影响。实际飞行过程中当空速因风速变化而变化时,飞控系统会通过调节N1来调节发动机推力,进而调节空速,使飞行空速与选择空速一致。而飞机的升力由空速和引角共同决定,在空速变化时,需实时调节俯仰角,从而保持升力稳定,所以在引入环境风后,空速、N1、俯仰角都随风速变化而变化。由图7可见引入环境风模型后的仿真曲线有明显的因风速变化而产生的振荡,与理论分析结果相符。

图7 飞行仿真结果

4 结论

本文中研究了基于QAR数据的环境风建模方法,将环境风模型划分为风速模块和风向模块。针对风速建模,考虑风廓线系数和季节之间的关系,提出具有季节特性的平均风建模方法。在紊流建模中,分析了紊流功率谱指数的分布范围,对传统紊流功率谱进行了扩展。针对风向建模,分析了风向和风速之间的相关性,提出了基于马尔可夫过程的风向建模方法。最后进行仿真实验,得到以下结论:

1) 平均风具有明显的季节特性,冬季风廓线系数明显大于夏季的风廓线系数。

2) 多数紊流的功率谱幂律指数不等于-5/3,本文中采用的数据集中,93.2%的实测紊流功率谱幂律指数在-1.98<λ<-1.13内。

3) 马尔可夫过程可以较好描述风向的变化特性,由于风向的稳定性和风速相关,所以不同风速下的风向变化应该用不同马尔科夫矩阵描述。

4) 风对飞行状态有明显影响。本文中提出的飞行仿真中的环境风仿真方法能够增加飞行仿真的真实度。