多级同步感应线圈装置温升计算方法优化研究

郑方正,黄垂兵,姜润翔,鲁梦昆,岳非弘

(海军工程大学 电气工程学院, 武汉 430000)

0 引言

线圈温升来源于放电电流产生的焦耳热,电枢温升来源于涡流效应,可能出现线圈温升过高导致环氧树脂绝缘层破裂或局部温度过高使电枢熔化的[1-4]情况,从而影响发射性能,因此电机温升成为了关注与研究的焦点[5-7]。文献[8]基于电流丝法计算多级同步感应线圈炮电枢温升,对比各部件温升变化;文献[9]基于comsol双向耦合计算电磁感应线圈发射器温升变化;文献[10]基于ansys单向耦合对同步感应线圈磁场-温度场进行分析,忽略了温升对材料属性的影响。

上述文献对发射电机温升方法进行研究,但存在瞬态温度场仿真存在计算时间长,剖分精度对温升结果影响较大等问题;电流丝法模型存在搭建过于繁琐,难度大等问题。鉴于以上问题,为找到一种快速计算发射电机温升的方法,提高计算效率,本文尝试将一维热网络模型[11-13]应用于同步感应线圈发射装置,以3级发射线圈为例,结合不考虑散热情况下的理论分析;瞬态热有限元仿真2种方法,对比仿真结果,验证一维热网络模型可行性。

1 数学模型

发射过程中同步感应线圈发射装置的温度场属于瞬态温度场。电磁感应线圈发射装置本身是一个有热源的导热体,主要是通过热对流和导热方式将热量传递到线圈发射器中,该过程是对流换热和热辐射的综合过程[14-16]。

1) 对流换热

对流换热是指流体流经固体时流体与固体表面之间的热量传递现象。对流换热依靠流体质点的移动进行热量传递的,与流体的流动情况密切相关。对流换热的主要影响因素是h强制h自然。

对流换热的强度依据牛顿冷却定律[6]:

q=hS(T-Tf)

(1)

式中:q为单位面积的固体表面与流体在单位时间内交换的热量,称作热流密度;T、Tf分别为固体表面和流体的温度;h为传热系数,反映对流换热的强弱。

2) 热辐射

热辐射就是以电磁波的方式传播,但是电磁波的速度很快,必须要通过媒介才能在一定程度上吸收热量。它不依赖于分子间的冲撞,也不依赖于气体和液体的流动,通过自己的体温把能量直接释放出去,这就是所谓的热辐射。

斯特番-波耳兹公式为

(2)

式中:q为热流密度;v为表面系数;σ为黑体辐射常数;T为发热体表面温度;T0为周围介质绝对温度。

1.2 发射电机参数

应用Maxwell 2D仿真环境,根据模型仿真结果,导入到瞬态温度场进行仿真。三级同步感应线圈发射装置的仿真参数见表1所示。

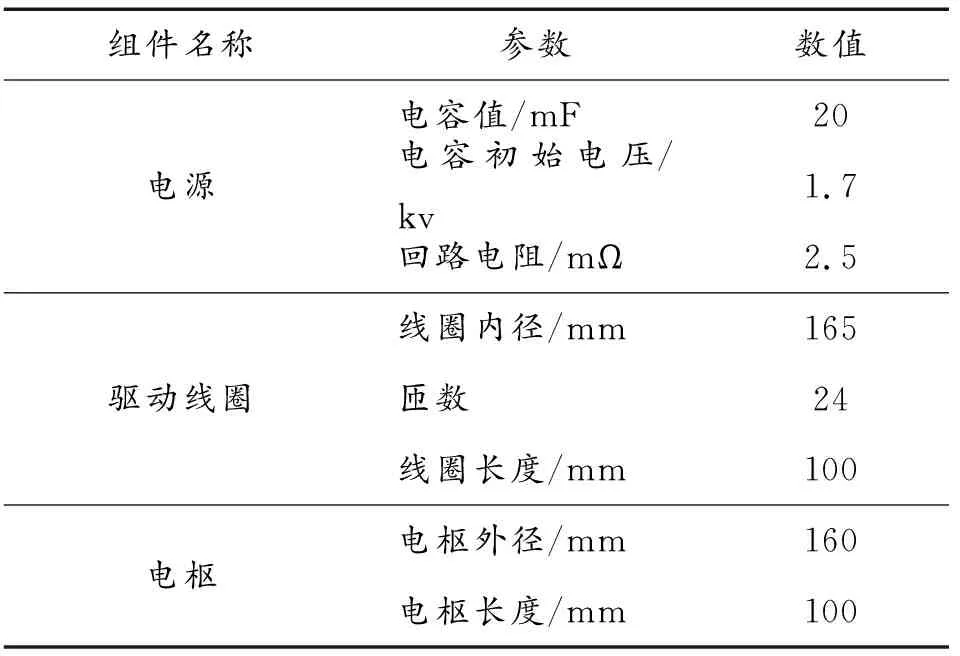
表1 模型参数

2 基于不考虑散热的理论温度分析

同步感应线圈发射装置设计初期,为摸底设计参数的合理性,考虑完全不散热的情况下理论计算电机温升,前提是电枢与绕组不与外界有热交换且热量在物体内的传递时均匀的,理论计算公式如下:

cωhLρΔT=I2Rt

(3)

(4)

其中:ΔT为线圈温升;I为电流密度;c为比热容;ρ为铜密度;ω为等效后线圈截面积长度;h为等效后线圈截面积高度;L为等效后线圈长度;β为电阻率;I为放电电流大小;R为线圈内阻。

电枢的温升计算方法分别根据公式

(5)

式中:W为电枢涡流损耗;c为铝材质比热容;m为电枢质量。

在不考虑散热时理论计算结果如图1、图2所示,三级线圈放电电流如图3所示。

图1 电枢温升曲线

图2 各级驱动线圈温升曲线

图3 三级线圈放电电流

由图1可知:电枢温升逐渐上升到32.1 K后趋于平缓;由图2可知:第1级线圈温升为3.1 K,第2级线圈温升3.2 K,第3级线圈温升达到3.7 K,随着级数的增加,线圈温升逐级增加,这是因为由线圈放电电流波形知,随着级数的增加,电流下降越缓慢,对应级数线圈铜损越多。

3 基于有限元多物理场温度分析

为一维热网络模型计算结果提供参考对比,考虑对流换热系数,借助ANSYS软件进行电磁场仿真,在ANSYS-workbench平台将电磁模块参数导入温度场中,建立发射电机Maxwell-thermal多物理场仿真模型,对系统的发热和散热进行精准计算。发射电机处于电磁场、运动场、温度场耦合环境,耦合流程如图4所示。

图4 温度场路耦合流程图

Ansys有限元属于单向耦合,将maxwell的计算结果导入到瞬态热中的,计算过程中物性参数并不会随着温度的变化而变化,载荷如图5所示。

图5 发射电机损耗

在初始温度22 ℃下,三级线圈温度分布如图6(a)—图6(c)所示。

仿真结果表明:第1级最高温度为24.806 K;第2级最高温度为24.872 K;第3级最高温度25.578 K。随着级数的增加,各级驱动线圈的温度逐渐增加,有限元温升结果与理论计算结果相差不太,但仿真时间过长,且网格剖分精度对仿真结果影响较大。

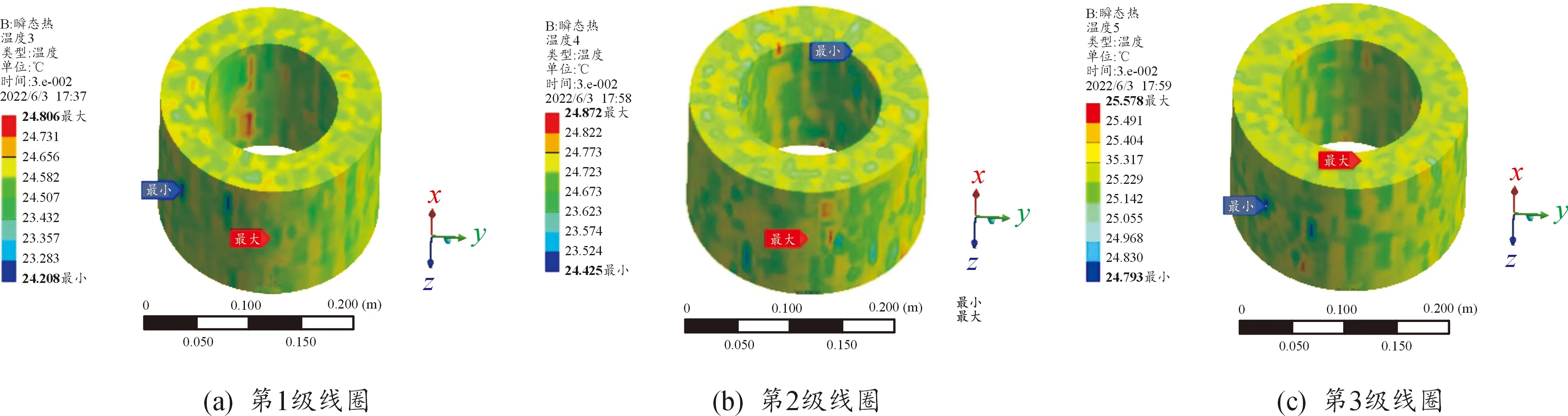
图6 三级发射线圈温度分布

4 基于一维热网络温度场分析

为解决瞬态热有限元仿真时间过长,提高计算效率,且网格剖分精度对发射性能影响很大等因素,将一维热网络模型计算方法应用于多级同步感应线圈装置中。一维热网络模型时将系统中具有传热,发热的元器件等效为电路中的热阻,该部分为传热网络,再将传热路径上的温差等效为电压,该部分叫做电路网络。这种算法最大优势在于大幅度减小计算时间,将电机发热等效成一维传热问题,推导发射电机状态方程,通过Matlab构建发射电机的一维热网络模型。

4.1 一维热网络模型

为简化计算流程且系统发射过程为ms级,忽略电枢与内壳间1 mm空气间隙,系统一维热网络模型剖面等效如图7所示。

图7 发射电机剖面图

将发射电机的温升计算模型简化为一维传热问题。瞬态热网络模型如图8所示(绕组与内壳间的热阻是绕组与绝缘串联等效后的热阻,绕组绝缘密度较小只考虑热阻不考虑热容)。

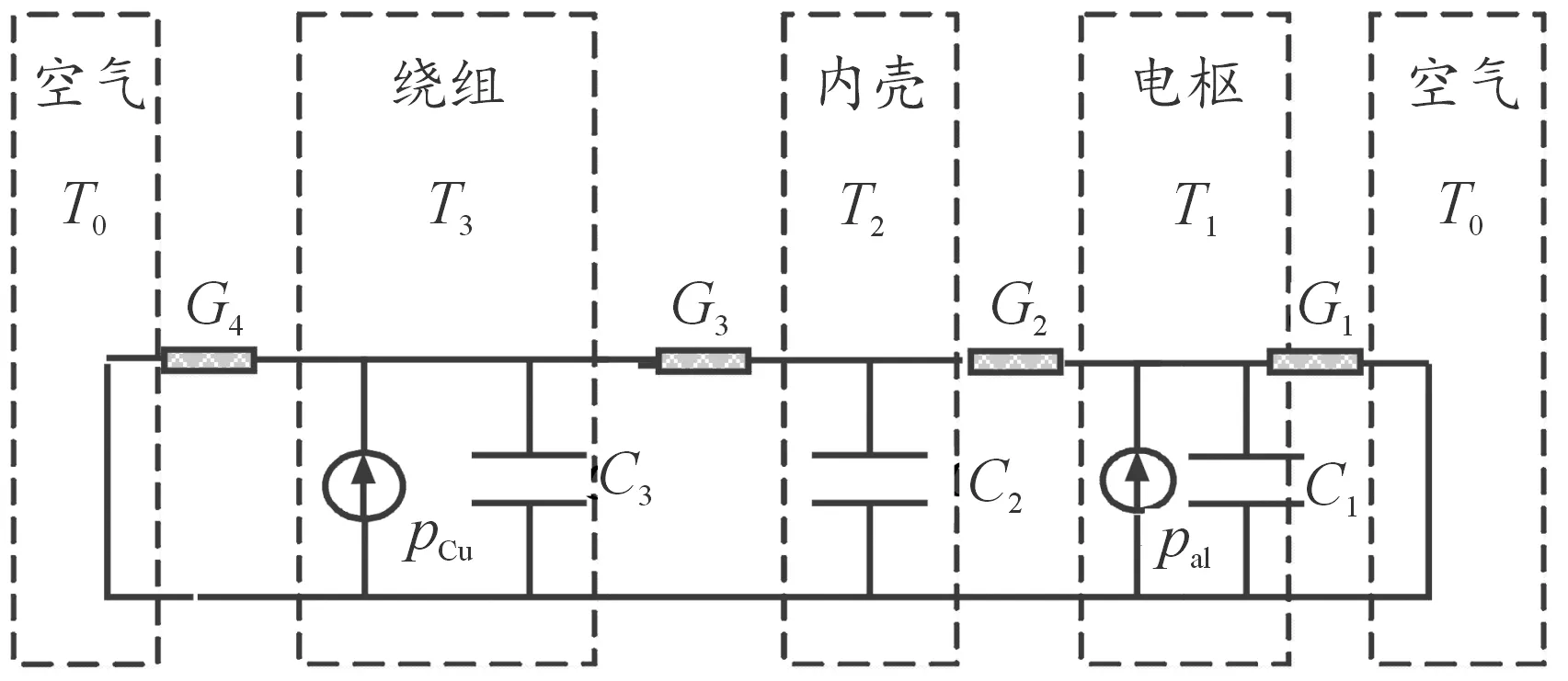
图8 瞬态热网络模型

表2 瞬态热网络模型中的符号说明

图8中瞬态热网络模型可以列出如下状态方程:

其中:pCu(t,T)为发射过程中绕组的铜耗;pAl(t,T)为电枢的涡流损耗。

4.2 模型散热系数及导热系数的确定

1) 空气与系统内外表面对流换热系数

对流换热系数是指两接触面单位时间温度相差1 ℃时对流换热而交换的热量。该系数与流体流速密切相关,模型发射过程ms级,属于强制对流阶段,对流系数为100 W/(m2·K);当电枢出膛后,线圈温度自然冷却,属于自然对流阶段,对流系数为5～25 W/(m2·K)。

2) 系统物性参数

表3 动子各层材料的物性参数

4.3 建模计算流程

5.1推导出发射电机状态方程,通过Matlab搭建发射电机模型,如图9所示对搭建流程简要介绍。图9中:R为各层材料热阻;L为各层截面积长度;S各层接触面面积;ρ为电阻的电导率;G为热导。

图9 一维热网络模型搭建流程图

简要思路为通过结构参数计算出各部件热容,再计算出对应层接触的热阻,因为任何一个接触面会向左右两边传递热量,热路间节点代表各层的平均温升,因此节点左右热路上热阻阻值为R/2,同时相邻热路上2个热阻为串联关系,串联热阻的热导公式可表示为G=1/(R2/2+R1/2),最后将计算的热容及热导值代入推导的状态方程中求解各层温升。

4.4 仿真结果

单次发射工况下,一维热网络模型仿真结果如图10、图11所示,并将一维热网络模型结果与理论结算结果对比,验证模型搭建的可行性。

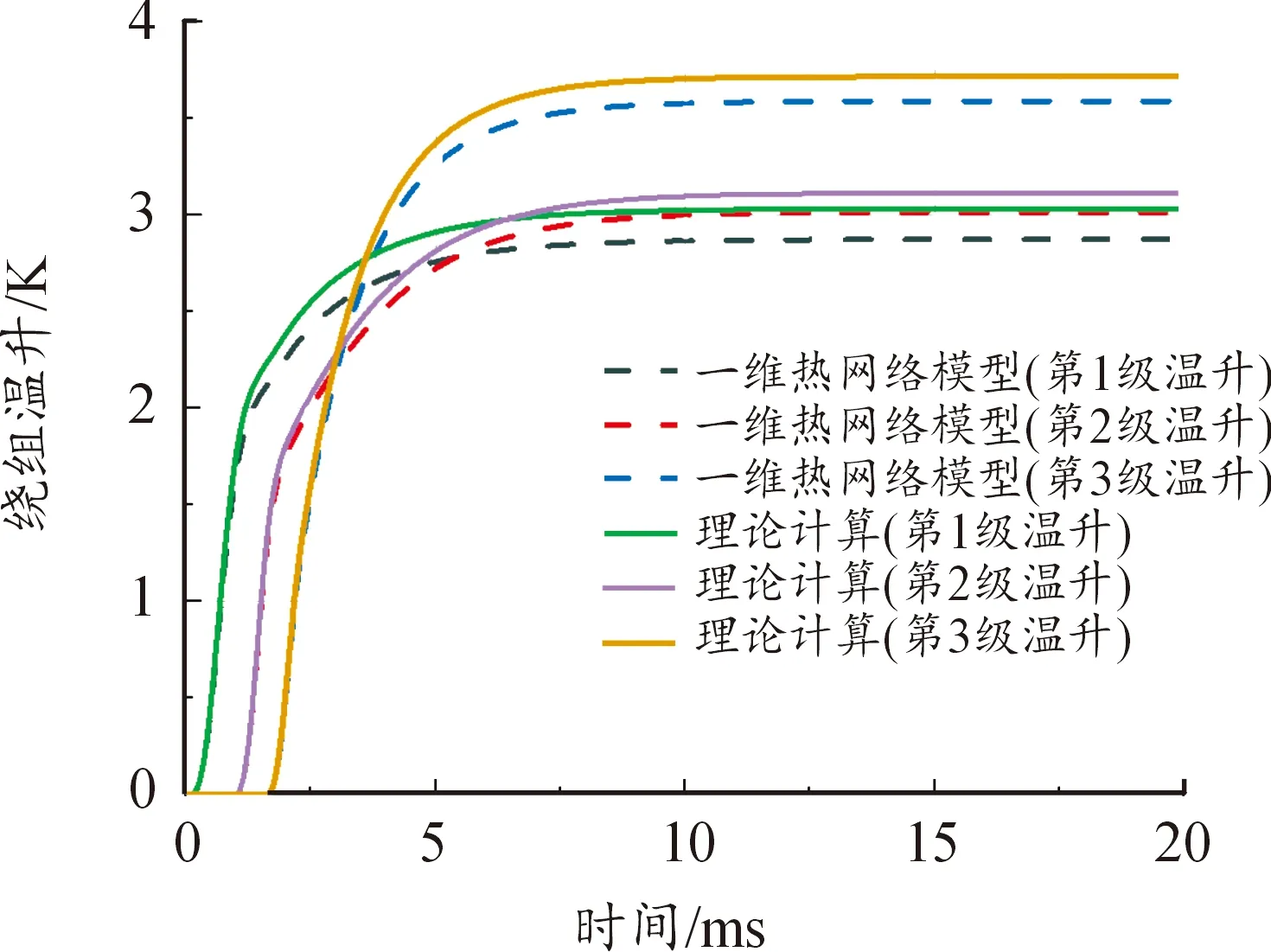
图10 各级线圈温升曲线

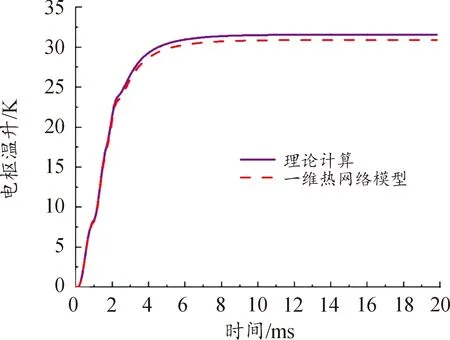
图11 电枢温升曲线

由图10各级线圈温升知,一维热网络模型计算结果中第3级线圈温升3.6 K,可忽略线圈自然散热过程;由图11电枢温升知,电枢经过三级发射系统加速后,平均温升达到31.1 K。一维热网络模型计算结果与理论计算及瞬态热有限元仿真结果对比,通过公式理论计算或有限元的最高温升减去一维热网络模型的最高温升,再除以理论计算或有限元最高温升结果,误差控制在10%以内,验证了一维热网络模型的正确性。

5 结论

1) 针对瞬态热有限元仿真时间过长,网格剖分精度影响大等问题,将一维热网络模型方法应用于同步感应线圈装置中,建立瞬态温升计算的热网络模型,并将计算误差保持在5%以内。

2) 一维热网络模型不仅减少了模型搭建难度,且显著提高了发射电机温升计算效率。