双层增强型爆炸反应装甲抗破甲能力数值模拟研究

2023-05-31胡亚峰陈维波李景荣徐宏林

兵器装备工程学报 2023年5期

胡亚峰,陈维波,李景荣,张凯,徐宏林

(中国华阴兵器试验中心, 陕西华阴 714200)

0 引言

20世纪70年代,爆炸反应装甲(explosive reactive armor,ERA)最早由M.Held教授发明,因为其携带方便、成本低廉、并且具有较好的抗破甲、抗穿甲能力,逐渐成为坦克等装甲车辆的主要防护手段。目前新型爆炸反应装甲主要以“钢板-炸药-钢板”的三明治结构为基础,采用双层平行或双层楔形的布局方式进行模块化组合,关于单层爆炸反应装甲(以下简称ERA)抗弹机理的研究比较广泛[1-5],而双层ERA的研究相对较少。M.Held[6]在2001年对带有单层或双层ERA的首上装甲、炮塔装甲和侧装甲进行抗击破甲战斗部试验,发现ERA抗击破甲战斗部的能力与法向角密切相关,且双层ERA较单层有更好的防护效果。黄正祥等[7]采用数值模拟方法对双层平行ERA引爆后各抛板的作用规律进行初步分析。姬龙等[8-9]对双层ERA不同楔形角条件下,金属抛板飞离弹轴线所需时间进行研究,为后级战斗部起爆延时设计提供了参考。张明等[10]采用数值模拟方法研究了着靶点位置对双层楔形装药反应装甲干扰射流的影响。

如今,随着串联破甲战斗部前级装药口径不断增大,以及末端弹道和前后级延时起爆参数的不断优化,传统单层或双层爆炸反应装甲的抗弹能力显著下降,已经无法应对新型反装甲弹药的威胁和挑战。双层增强型ERA则是通过高强度钢屏蔽层降低前级射流起爆能力,通过金属隔板增强后端切割干扰能力,尽可能保证在一定角度范围内,前级只能消耗第1层反应装甲,让主级射流难以逃避第2层反应装甲的干扰。到目前为止,双层平行组合ERA是主流设计方案[11-14],但国内外关于复杂组合形式的双层ERA研究较少。为了进一步挖掘反应装甲的抗弹能力,基于模块化组合的思想,构建了双层增强型爆炸反应装甲模型,采用非线性动力学计算程序LS-DYNA,对其在0°、22°、45°、68°等4种侵彻角度下抗击某型制导弹药前级战斗部的能力进行数值模拟研究,对钢板抛掷、切割、扰动射流的过程进行定量计算,最后通过实弹飞行破甲试验对数值模拟计算结果进行验证。

1 计算模型与参数

1.1 模型的建立

双层增强型ERA主要由高强度装甲钢盖板、平行双层ERA和隔板组成,其中每个ERA均采用4 mm/7 mm/4 mm的三明治结构,如图1所示,从上到下依次为盖板、ERA-1面板、ERA-1夹层炸药、ERA-1背板、隔板、ERA-2面板、ERA-2夹层炸药、ERA-2背板和主装甲,其具体结构参数如下:盖板、面板、背板、隔板均采用高强度装甲钢,其中盖板厚度为15 mm;面板、背板、隔板厚度均为5 mm;夹层装药为PBX炸药,装药质量为300～360 g;盖板与ERA-1间距15 mm,隔板与双层ERA间距10 mm,ERA-2与主装甲间距20 mm。破甲战斗部采用某型制导弹药串联战斗部前级聚能装药,最大装药口径65.8 mm,炸药为8701炸药,药型罩材料为紫铜,采用中心点起爆方式。

图1 双层增强型反应装甲结构

采用TrueGrid软件建立1/2三维数值模型,在k文件中编辑*INITIAL_VOLUME_FRACTION_GEOMETRY关键字,定义炸药、药型罩和ERA夹层炸药的物质边界,炸药、药型罩和ERA夹层炸药和空气介质都采用ALE算法,编入一个多物质欧拉组,反应装甲钢板结构采用拉格朗日算法,两者之间应用流固耦合算法,在对称面设置对称约束,在空气外围设置自由流出边界,仿真计算模型如图2所示。

图2 有限元模型示意图

1.2 材料模型及参数

聚能战斗部的炸药采用高能炸药材料模型和JWL状态方程描述,具体参数见表1[16],其中ρ为密度;D为爆速;PCJ为爆轰波C-J面压力;A、B、R1、R2、ω为试验确定的常数;E0为单位体积的初始内能。紫铜药型罩采用Gruneisen状态方程和Johnson-Cook本构模型描述,具体参数见表2[16];炸药和药型罩材料参数均经过试验验证[15-16],满足计算精度要求。钢板采用Plastic-Kinematic模型,其中E为弹性模量,λ为泊松比,σs为材料的弹性屈服强度,C、P为材料应变率相关常数,β为随动硬化系数,fs为失效应变,具体参数见表3。反应装甲夹层炸药为PBX-9404,采用Lee-Tarver点火增长模型进行描述,该模型的反应速率方程为:

G2(1-λ)eλgpz

(1)

式中:λ为炸药气体质量与炸药总质量比,也称为反应度;ρ0为炸药初始密度;ρ为炸药当前密度;p为炸药爆轰压力;I、Gl、G2、a、b、c、d、e、g、x、y、z为12个可调参数。式(1)右边第1项为点火项;第2项为成长项,描述了热点向内外传递过程;第3项为快反应项,描述了燃烧快速向爆轰转变的过程。a为临界压缩度,当炸药压缩到某一值时点火开始,点火项是冲击强度和压力持续时间的因变量;b和c分别为点火项和燃烧项的燃耗幂数,参数x和I则控制了点火热点的数量,早期热点生长由G1和d控制,反应速率则由G2和z确定。当λ>λIGmax时,点火项停止;当λ>λIG1max时,燃烧项停止;当λ<λIG2min时,快速反应阶段完成,具体材料参数见表4[17]。

表1 8701炸药材料参数

表2 紫铜材料参数

表3 钢板材料参数

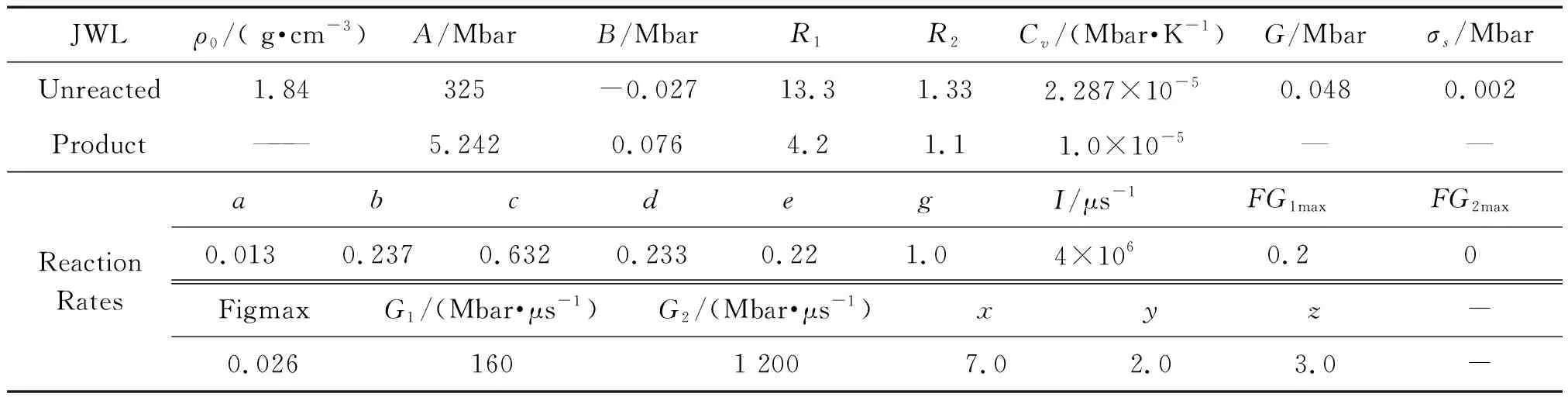
表4 PBX炸药Lee-Tarver点火增长模型参数

2 冲击引爆效果及射流受干扰情况分析

构建了0°、22°、45°、68°等4种侵彻角度(射流轴线与靶面法线夹角)下的数值计算模型,聚能射流对双层增强型反应装甲的冲击引爆情况如图3所示,具体计算结果如表5所示。0°和22°侵彻,射流可以引爆并击穿双层ERA;45°侵彻,虽然可以引爆双层ERA,但难以击穿第2层ERA,并且其引爆第1层ERA的Held判据值已经下降到22 mm3/μs2,接近冲击引爆的临界值[18],由于受到爆炸产物横向冲击和钢板切割的双重作用,射流形态紊乱,较初始轴线发生较大偏移,t=246 μs时刻,最大速度已经降至921 m/s,侵彻能力显著下降,此时尚未击穿ERA-2背板。由此可以判断,当侵彻角度大于45°时,引爆第2层ERA的难度会逐渐增大;68°侵彻,射流只能引爆第1层ERA。

侵彻角度的变化,对射流速度、射流形态有较大影响。主要是因为炸药爆轰、爆炸产物冲击以及钢板的切割在不同角度下的作用效果有较大不同。图4给出了不同侵彻角度射流头部速度随时间变化曲线,侵彻角度为45°时v-t曲线下降最快,侵彻角度为0°时v-t曲线下降最慢,由于68°角侵彻,第2层ERA没有被引爆,因此v-t曲线下降速率略低于45°侵彻。在双层反应装甲均引爆的情况下,射流头部速度的下降速率随着角度的增加而增加。图5给出了击穿盖板、ERA1、ERA2的残余射流随侵彻角度变化曲线,由图5可以看出,残余射流速度随侵彻角度的增加而逐渐降低,且下降速率越来越大,接近于指数衰减。当侵彻角度≥45°,残余射流难以从ERA2作用场中逃逸,当侵彻角度≥68°,残余射流难以从ERA1作用场中逃逸。

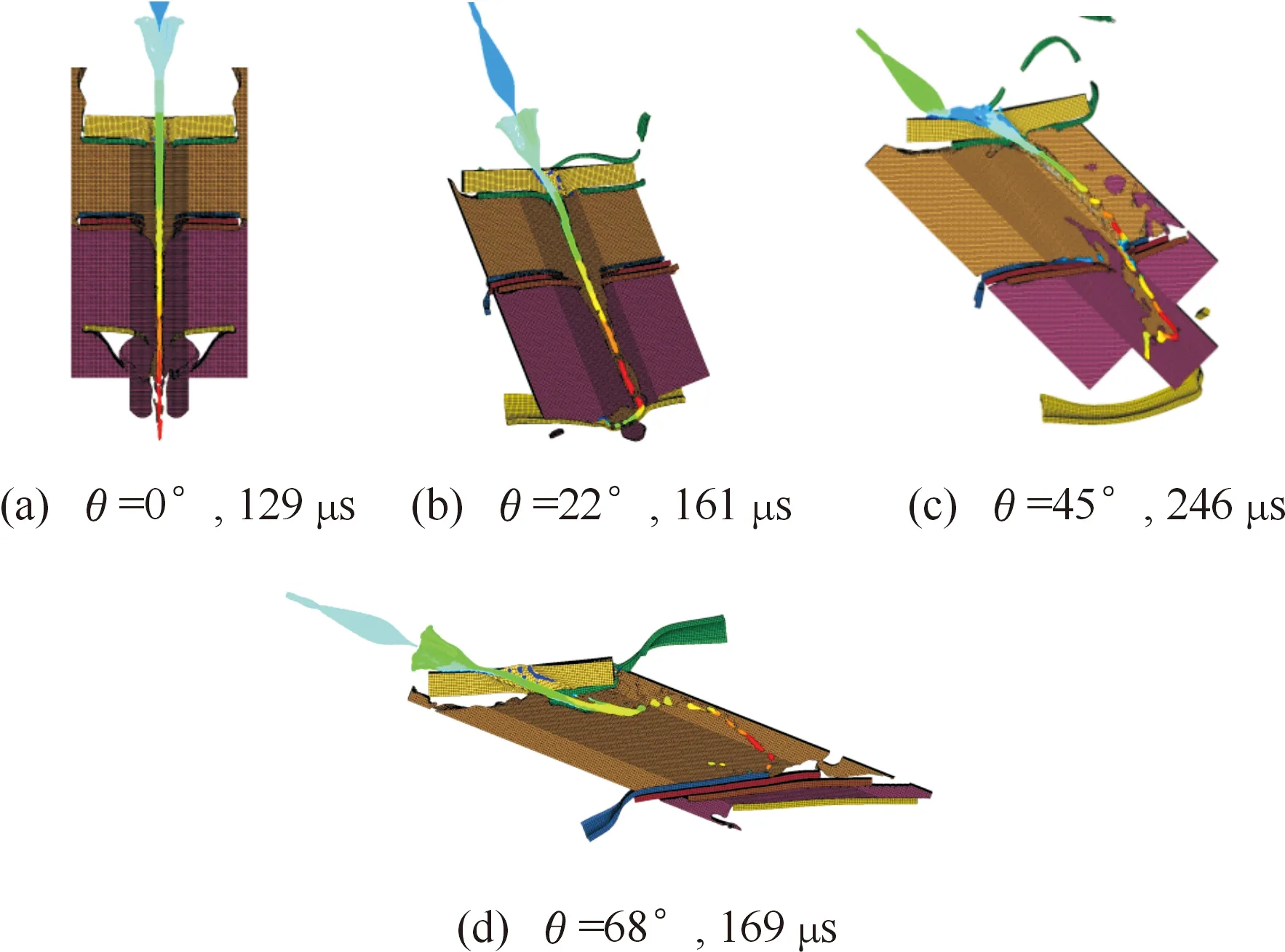
图3 不同角度侵彻射流干扰形态

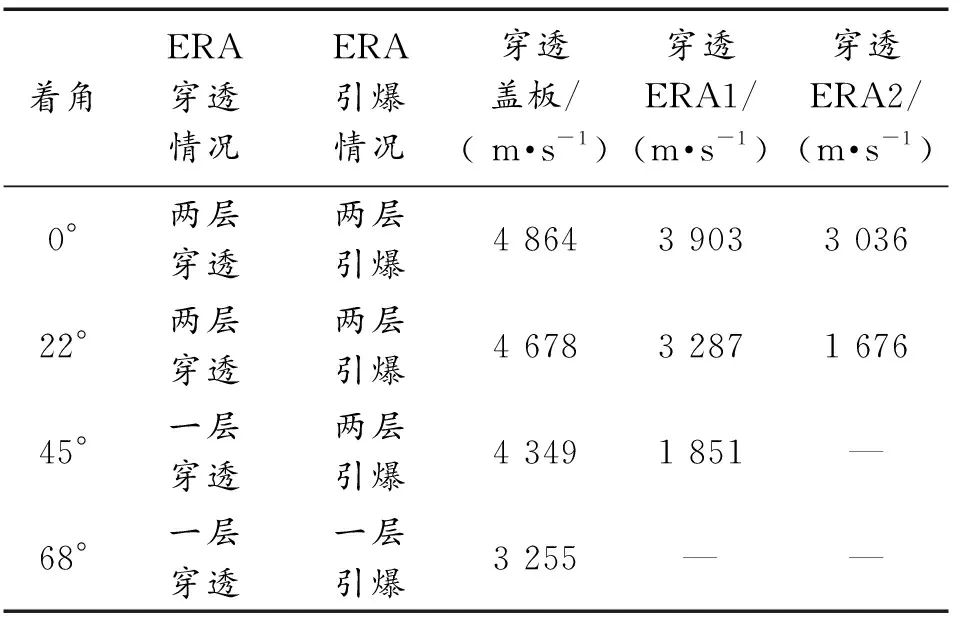
表5 数值模拟计算结果

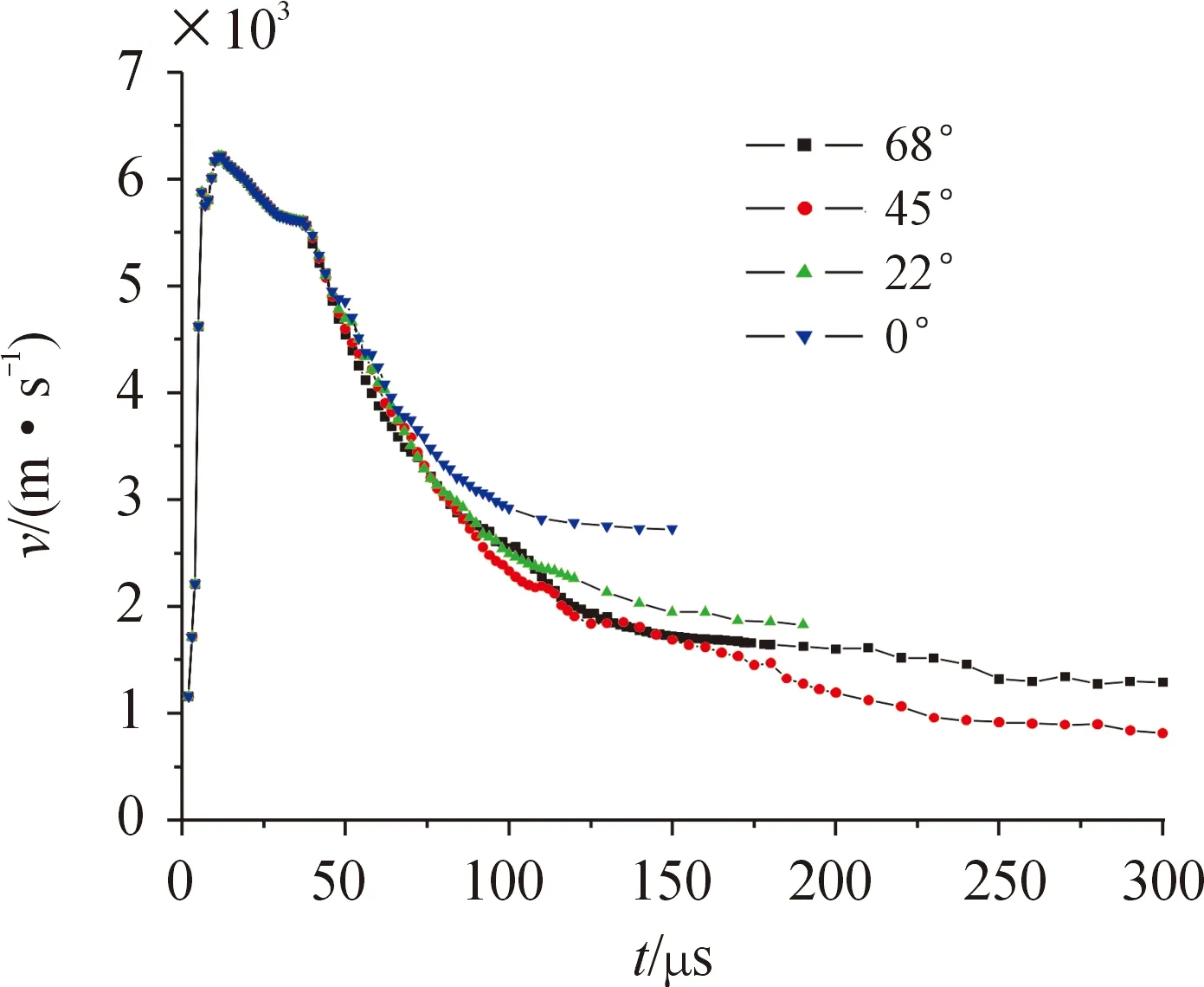
图4 不同侵彻角度射流头部速度变化曲线

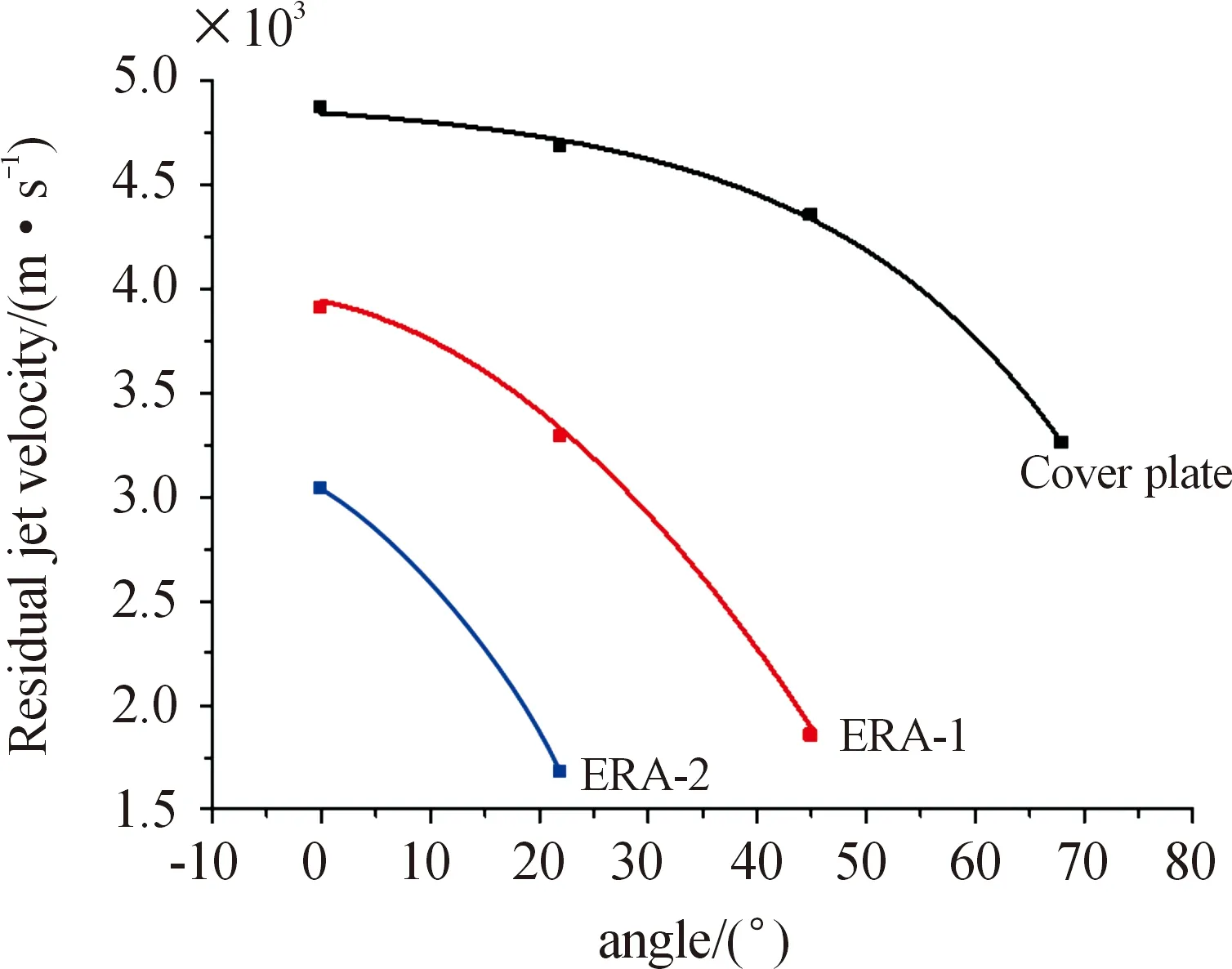
图5 残余射流随侵彻角度变化曲线

侵彻角度变化对射流形态影响最大,最终影响战斗部的毁伤效能。图6为不同侵彻角度射流轴线偏离程度随时间变化曲线,0°侵彻几乎没有任何轴向偏移,22°侵彻轴向偏移还不太明显,双层ERA对轴向偏移的作用界限也不清晰,线性拟合度良好。45°侵彻轴向偏移已经十分明显,双层REA对轴向偏移的作用界限清晰,2次作用的曲线的斜率相近,这里主要对第2层作用过程进行线性拟合。68°侵彻虽然只有第1层ERA作用,但轴向偏移却非常明显。对不同侵彻角度的轴向偏移量进行线性拟合,得到的斜率即为不同角度下射流的横向偏移速度,如图7所示,该横向偏移速度随侵彻角度变化应服从指数分布。拟合得到某型制导弹药前级射流横向偏移速度Vlateral随侵彻角度θ变化公式为:

Vlateral=77eθ/33-82

(2)

式中:Vlateral单位为m/s;适用范围0°<θ<90°。该公式对于判断某型制导弹药前级射流不同角度侵彻时轴线偏移程度具有参考价值。

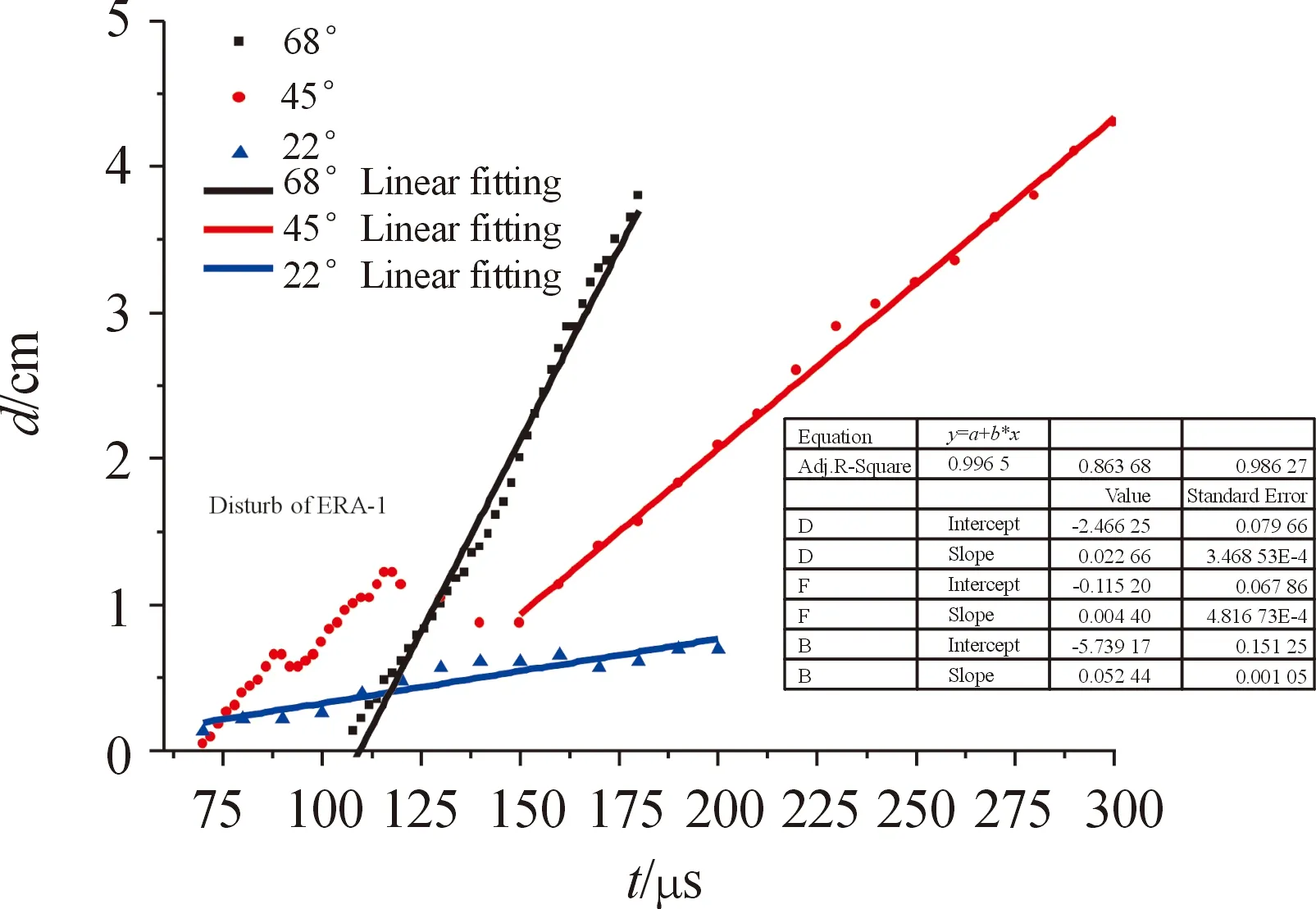
图6 不同侵彻角度射流轴线偏离度

3 钢板抛掷与射流切割规律分析

聚能射流穿透金属板并击中高能炸药层,炸药迅速爆轰,在爆轰产物压力作用下,金属板获得较大加速度,并沿板表面法向方向运动,运动速度与夹层炸药质量和金属板质量的比值有关(Gurney模型)。金属抛板对射流具有较强的切割作用,其干扰射流的过程可分为2个阶段[19]:射流高速段产生断续干扰(卵石模型),射流低速段产生连续干扰(稳定干扰)。反应装甲各钢板抛掷速度时程曲线如图8所示,“上切下挡”连续干扰示意图(45°)如图9所示。

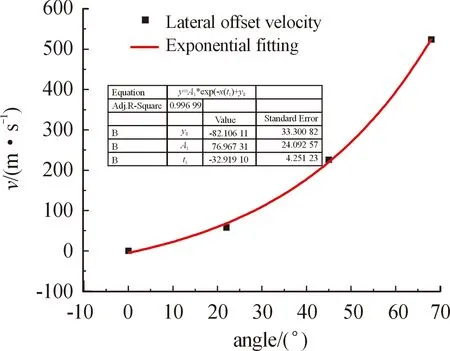
图7 横向偏移速度随侵彻角度变化曲线

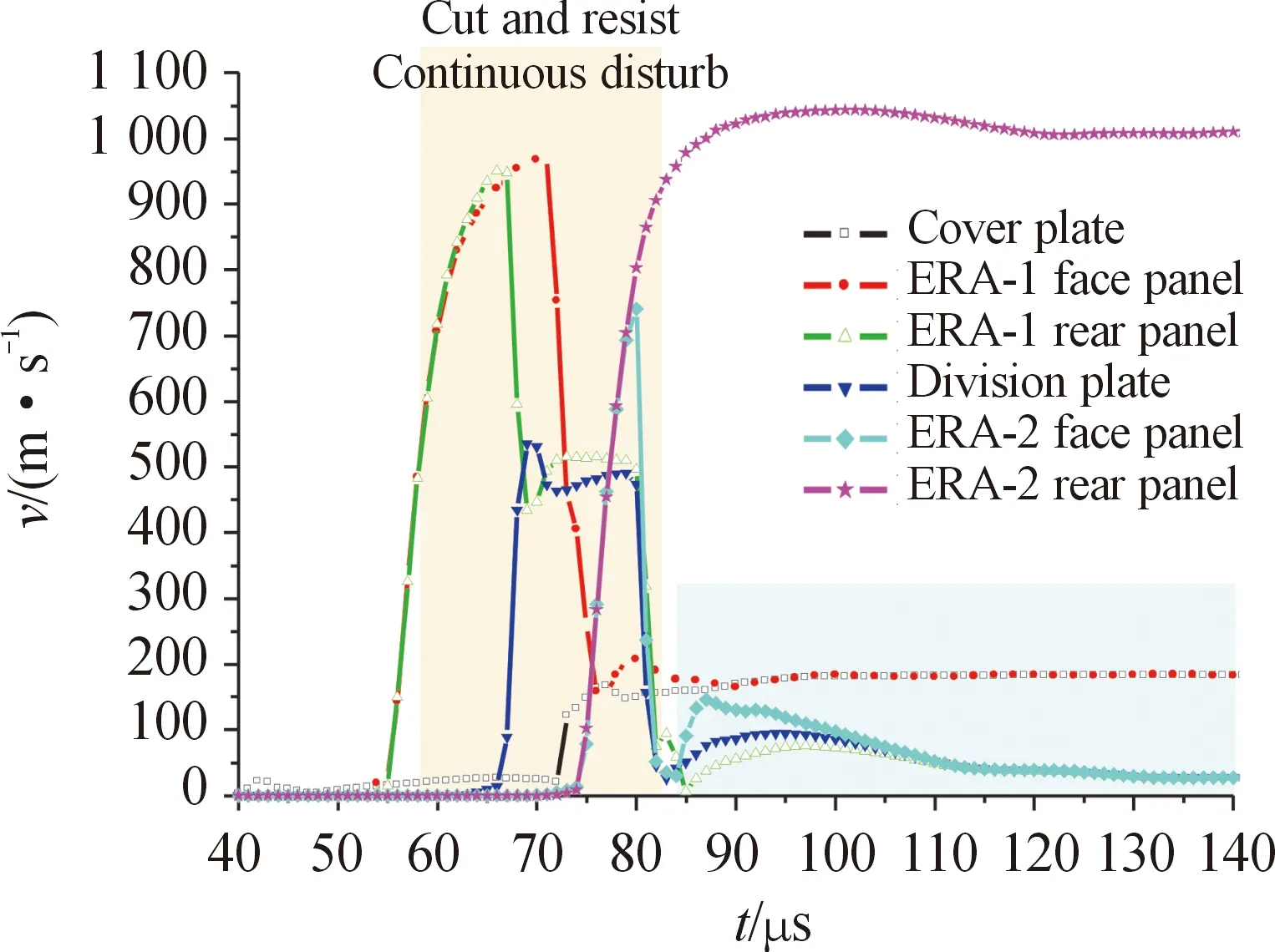
图8 反应装甲各钢板抛掷速度时程曲线

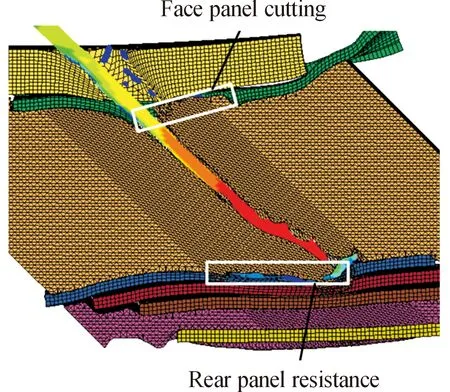
图9 “上切下挡”连续干扰示意图(45°)

由图8可以看出:t=67 μs时,ERA-1背板以950 m/s的速度撞击隔板,两者质量相当,经过13 μs的阻尼震荡,最终以480 m/s的速度向下运动;t=80 μs时,ERA-2面板在加速阶段以738 m/s 的反向速度与ERA1背板和隔板相撞,三者最终速度稳定在40 m/s;t=71 μs时,ERA-1面板以970 m/s的速度撞击盖板,两者最终以180 m/s的速度沿法线方向抛掷;由于没有设置主装甲,ERA-2背板抛掷速度最终稳定在1 015 m/s,若设置主装甲其速度将骤然下降。在钢板运动规律确定的情况下,侵彻角度越大,越容易形成连续干扰,由图9可知,ERA-1面板向上运动不断切割射流,形成一个长条形的切割区域,ERA-1背板向下运动,与射流头部不断更换碰撞位置,形成一个长条形的阻挡区域。

计算结果显示:角度侵彻在45°以上,t=58～82 μs,钢板运动速度较高,基本上满足连续干扰模式,持续时间为20～30 μs;随后各钢板的速度均显著下降,将会进入“卵石”断续干扰阶段。

表6 给出了不同侵彻角度各层钢板切孔长度的仿真计算结果,由表6可以看出,随着侵彻角度增大,ERA-1面板、背板切割长度不断增大,而隔板、ERA-2面板的切割长度在侵彻角度从22°增加到45°时,反而出现了下降,这是因为在大角度下射流受第1层ERA干扰明显,射流侵彻能力大大下降,难以有效切割后续钢板。此外为了提高计算效率,模型没有设置主装甲,因此45°侵彻时,ERA-2背板无障碍抛掷,导致切割长度为0。

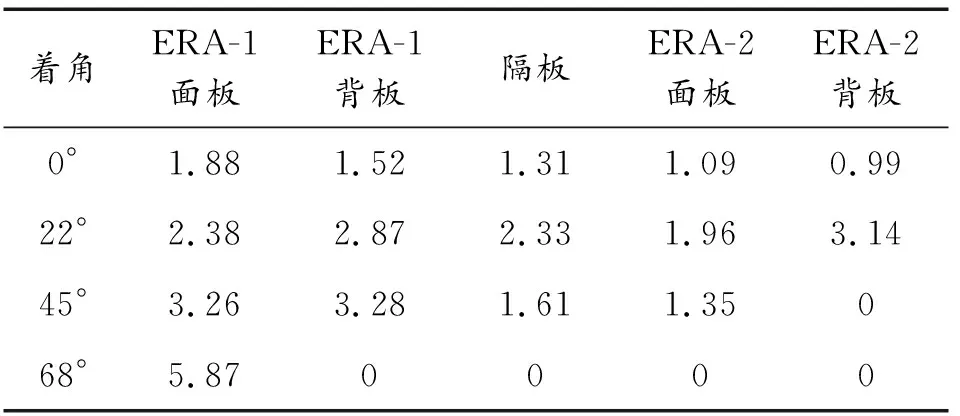
表6 不同侵彻角度钢板切孔长度(cm)

4 飞行破甲试验验证

采用某型制导弹药对铺设双层增强型反应装甲,且法线角为68°的钢板靶进行实弹射击,采用高速录像拍摄终点中靶姿态,测试所得落角为21.5°,弹体侵彻角度为46.5°,实验结果显示后级战斗部射流无障碍穿透主装甲,现场毁伤情况如图10所示。图10(a)为反应装甲底壳残骸,内部共装有4个双层增强型ERA单元,左下角发黑区域为双层增强型ERA单元被引爆后ERA-2背板撞击的痕迹,可以看出其余3个ERA单元并未发生殉爆,底壳中间的裂缝为背板撞击撕裂所致;由图10(b)可知,可以在钢板靶上看到ERA-2背板撞击痕迹和主射流穿孔,但未发现前级射流残骸和穿孔痕迹。