基于裂缝诱导应力场的套管应力影响因素分析

杨钊 孙锐 梁飞 刘照义

摘要：水平井分段压裂形成人工裂缝，产生的裂缝诱导应力场影响套管应力分布。为研究在裂缝诱导应力场作用下套管应力影响因素，基于理论公式和有限元分析方法，建立套管应力力学模型和裂缝-地层-水泥环-套管三维有限元模型，借助力学模型验证有限元模型的可行性，模拟岩石弹性模量、套管内壁压力、水泥环弹性模量、地应力变化和施工排量对套管应力的影响，并针对徐深气田实际压裂段进行实例分析。研究结果表明：当岩石弹性模量低于15 GPa时，套管发生塑性形变，套管内壁无压力加剧了套管塑性变形程度；当套管内壁压力为100 MPa时，水泥环软硬程度对套管应力基本无影响；套管应力随着水泥环弹性模量的增大呈现增大的趋势，水泥环泊松比和软硬地层不改变套管应力变化趋势；随着地应力差值的增大，套管应力呈现减小的趋势；施工排量为16 m3/min时，套管存在塑性变形，达到极限施工排量18 m3/min时，套管完全失效。研究成果对压裂段套管的损坏防治具有一定的指导意义。

关键词：水平井；压裂；套管应力；裂缝诱导应力；施工排量；套管内壁压力；施工排量

The staged fracturing of horizontal well creates artificial fractures， and the resulting fracture induced stress field affects the distribution of casing stress.In order to identify the influential factors of casing stress under the action of fracture induced stress field， based on the theoretical formula and finite element analysis method， the mechanical model of casing stress and the 3D finite element model of fracture， formation， cement sheath and casing were built.With the help of the mechanical model， the feasibility of the finite element model was verified.The influences of rock elastic modulus， casing inner wall pressure， cement sheath elastic modulus， insitu stress change and pumping rate on casing stress were simulated.Finally， case analysis was carried out for the actual fracturing section of Xushen Gas Field.The study results show that when the elastic modulus of rock is lower than 15 GPa， plastic deformation occurs in casing， and the absence of pressure on the inner wall of the casing aggravates the plastic deformation of the casing.When the inner wall pressure of the casing is 100 MPa， the hardness of the cement sheath basically has no effect on the casing stress.The casing stress increases with the increase of the elastic modulus of the cement sheath， and the Poissons ratio of the cement sheath and the soft and hard strata do not change the variation trend of casing stress.With the increase of insitu stress difference， the casing stress shows a decreasing trend.When the pumping rate is 16 m3/min， the casing has plastic deformation；when the pumping rate reaches the extreme of 18 m3/min， the casing completely fails.The study results have certain guiding significance for the prevention and control of casing damage in fracturing section.

horizontal well;fracturing;

casing stress；fracture induced stress；pumping rate；inner wall pressure of casing；pumping rate

0 引 言

當前，常规油气资源已难以满足国际能源需求，高效开发非常规油气资源为能源供给提供了重要保障［1-3］。水平井压裂技术实现了非常规油气资源的经济开发。

在水平井分段压裂过程中，多段多簇裂缝产生叠加诱导应力，改变了套管周围原地应力场大小和方向，从而改变套管受力场［4］。

水平井分段压裂需要足够多的压裂裂缝，然而井内压力过高可能导致井壁形成纵向拉伸裂缝，与裂缝段连通后水力裂缝中的压裂液会挤压围岩进而产生诱导应力场［5-7］。尹建等［8］建立压裂过程中水力裂缝扩展诱导应力场计算方法，根据水力裂缝扩展过程中水平最大、最小主应力和诱导应力之间的关系，提出射孔间距优化方案。A.A.DANESHY［9］研究认为，压裂过程中产生的非对称裂缝对套管产生了拉伸和剪切作用，是套管发生挤压损坏的主要原因。练章华、于浩等［10-13］提出套管损坏是由于压裂过程中地层性质变化、压裂区域和地应力分布不均匀及施工压力大等因素共同作用下的结果。高利军等［14］认为天然裂缝越长，套管变形越严重，水泥环弹性模量对套管变形影响不大。刘伟等［15］认为，压裂过程中与套管相交的天然裂缝滑移是该致密油区区块体积压裂过程中套管变形破坏的主要原因。杨钊等［16］采用基于离散元分析方法，在不考虑套管内压的情况下，从二维平面角度来研究微裂缝形态变化对套管应力的影响。

近年来，国内外学者通过建立诱导应力计算模型及离散元分析方法来研究套管应力变化较多。其中离散元二维分析方法不能反映真实裂缝形态特征；而基于有限元分析方法，可建立接近压裂段裂缝特征的三维有限元模型，从而研究不同因素对套管应力的影响。但由于建模和计算难度等问题，相关研究成果较少。笔者采用有限元分析方法，通过建立裂缝-地层-水泥环-套管三维有限元模型，对套管应力分布进行数值模拟，得到岩石弹性模量、套管内壁压力、水泥环弹性模量、地应力场变化和施工排量等对套管应力分布的影响规律，并通过实际压裂段进行分析论证。

1 力学模型

1.1 裂縫诱导应力

诱导应力场会对临近储层产生影响，段数增多会对入靶点处套管受力变形产生累计效应。

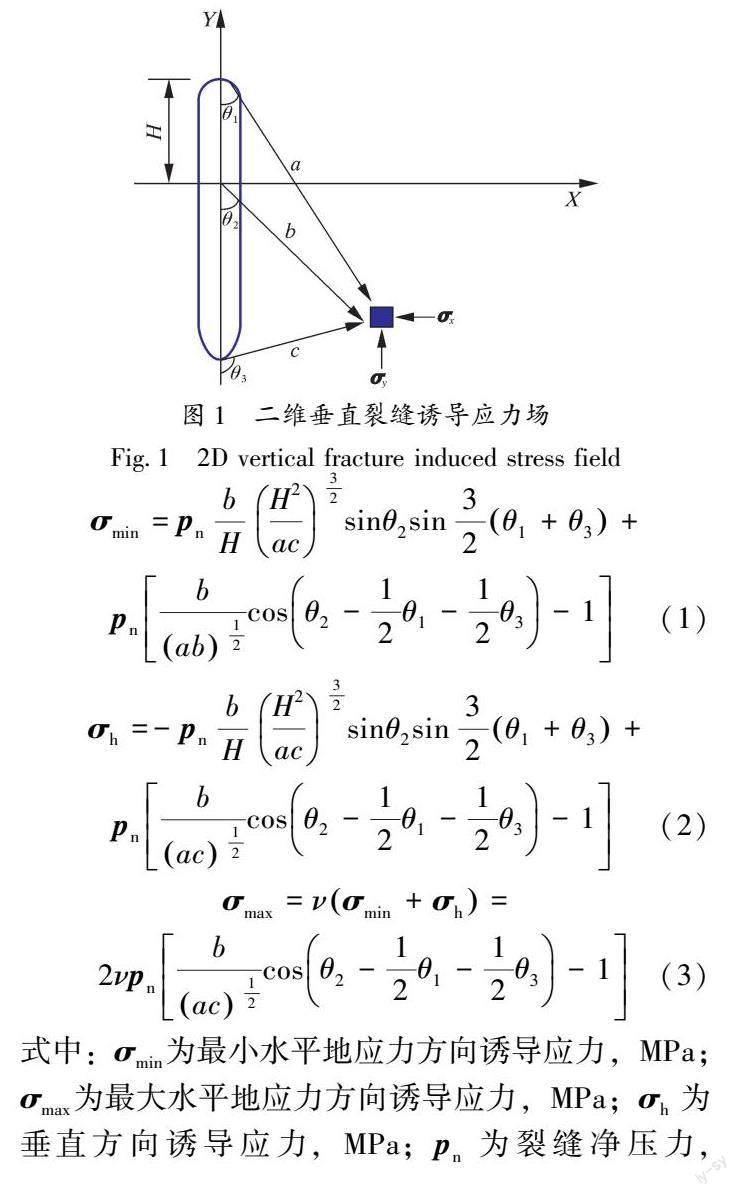
本文以均质、各向同性的二维平面应变模型为基础，建立二维垂直裂缝诱导应力场几何模型（见图1）。假设裂缝理想形态为宽度大、长度长的长窄缝，取拉负压正，二维平面内具有一定的净压力。根据Sneddon公式［17-18］，该净压力产生的平面内的诱导应力计算方法如下：

模型中水泥环外径215.9 mm，套管外径139.7 mm，套管内径121.36 mm。根据圣维南原理，地层模型长度到井眼距离取井眼直井的5倍以上，为此地层模型取2 m×2 m×2 m。

2.2 载荷施加与网格划分

给模型施加地应力，取垂向地应力σh=65 MPa、最大水平地应力σmax=60 MPa、最小水平地应力σmin=55 MPa。有限元网格模型全部采用六面体结构化网格进行计算分析，由于套管是主要的研究对象，所以对裂缝的网格尺寸进行粗化，提高模型的计算效率，网格划分结果如图3所示。

考虑裂缝内部含有高压的压裂液，因此在套管内壁与裂缝内部均施加70 MPa的压力，建立裂缝-地层-水泥环-套管三维有限元模型，如图4所示。

2.3 模型验证

基于裂缝-地层-水泥环-套管（压裂段）有限元三维模型和力学模型，模拟套管内壁压力pi从10 MPa到100 MPa变化，部分有限元模拟结果如图5所示，套管应力随pi变化规律如图6所示。

从图5可知，靠近裂缝射孔部位，套管应力越集中，近裂缝段应力较小，不易出现应力集中现象。

由图6可知，理论计算和模型模拟结果趋势一致，但二者存在一定误差，误差数值随pi的增大呈现增大趋势，但整体数值接近。理论公式验证了裂缝-地层-水泥环-套管模型可以用来模拟裂缝诱导应力对套管应力的影响。

3 套管应力影响因素

3.1 岩石弹性模量

岩石的弹性模量直接影响岩石的抗变形能力，若岩石越容易变形，则近井筒围岩对套管的挤压强度越强。为研究不同岩石弹性模量对套管应力的影响，设置岩石弹性模量变化范围为5～65 GPa，同时考虑当压裂过程中出现停泵现象，套管内壁压力会大幅度降低，为此设置套管无内压和内压70 MPa。当无内压时，不同岩石弹性模量下的径向应力、周向应力（取压裂段）和轴向应力云图如图7所示;套管应力随岩石弹性模量变化规律曲线如图8所示。

从图7可知：随着岩石弹性模量的增大，裂缝产生的诱导应力对地层-水泥环-套管组合体影响范围也随着扩大；套管径向应力和轴向应力集中部位从射孔部位向两侧移动，周向应力集中部位由整个壁面变为最大水平地应力方向套管内壁；岩石弹性模量较小时，套管的径向应力、轴向应力和周向应力大小整体接近，随着岩石弹性模量增大，套管周向应力与径向应力、轴向应力差异明显，周向应力降幅较大，套管破损不易出现在周向面。

从图8可以看出，套管应力随着岩石弹性模量的增大呈现减小的趋势。这是由于随着岩石弹性模量的增大，岩石抵御裂缝产生的诱导应力能力增强，承受了一部分本该作用在套管外壁的诱导应力和远场地应力；当套管内壁有液柱压力时，岩石弹性模量的变化对套管应力的影响较小，但高弹性模量的岩石有利于保护套管。当岩石弹性模量低于15 GPa时，无论套管内壁有无压力，套管应力都突破屈服强度，套管已然发生塑性变形，而套管内壁无压力加剧了套管塑性变形程度，因此需要避免出现停泵情况；岩石弹性模量高于35 GPa且套管内壁无液柱压力时，套管应力趋近稳定，远低于屈服强度，套管不易发生屈服破坏。

3.2 套管内壁压力

压裂施工通常会在井口使用较大施工压力使压裂液对岩石进行破碎从而达到造缝的目的，但这也对套管产生了巨大的内壁压力。为研究已压裂生成裂缝时，套管内壁压力变化对套管应力分布的影响，根据某井压裂时井底压力的变化情况，设置套管内壁压力变化范围为20～120 MPa，同时也考虑到水泥环软硬程度的不同，对套管的支撑与保护作用也有所差异，为此设置水泥环弹性模量分别为10 GPa（软水泥环）、50 GPa（硬水泥环）。当套管内壁压力为60 MPa时，径向应力、周向应力和轴向应力云图如图9所示;套管应力随套管内壁压力变化规律曲线如图10所示。

从图9可知：水泥环的软硬程度不改变套管应力集中部位，但水泥环越硬会使水泥环承受更多来自裂缝产生的诱导应力；轴向应力随着水泥环弹性模量的增大，压裂段套管由套管外壁变为内外壁均出现应力集中。

从图10可知，套管应力随着套管内壁压力的增大而增大，而水泥环的软硬程度不影响套管应力变化趋势。当套管内壁压力相同时，随着水泥环越硬，套管应力降低，这是由于较硬的水泥环对来自地层附着于井筒的载荷缓冲能力不足，但套管内壁存在液柱压力，通过射孔与裂缝相联通，在一定程度上抵消了來自地层的载荷，水泥环起到了支撑与保护作用。当套管内壁压力增大至100 MPa时，水泥环软硬程度对套管应力基本无影响，套管内压超过100 MPa且水泥环弹性模量较大，套管应力随着套管内压的增大增幅较小，套管应力保持稳定。

3.3 水泥环弹性模量

作为保护套管的重要屏障，水泥环的质量对套管强度安全性的影响至关重要。水泥环弹性模量的大小决定水泥环的软硬程度，同时一方面水泥环的泊松比也影响其疏松、破碎程度，另一方面地层岩石弹性模量不同导致有软硬地层之分。为此设置水泥环弹性模量变化范围为5～30 GPa，以5 GPa的幅度进行递增，水泥环泊松比分别取0.12和0.32，岩石弹性模量分别取15 GPa（软地层）和55 GPa（硬地层）。当水泥环弹性模量为13 GPa，水泥环泊松比分别为0.12和0.32时，对应的模拟结果如图11所示；在不同水泥环泊松比情况和软硬地层条件下，套管压力随水泥环弹性模量变化曲线如图12所示。

从模拟结果（见图11）可以看出：水泥环泊松比的增加不改变套管应力集中部位，径向面的应力主要集中于压裂段套管内壁；当水泥环弹性模量为15 GPa时，套管径向应力随着水泥环泊松比增大至0.32达到屈服强度，套管开始由弹性变形转为塑性变形。

从图12可知，套管应力随着水泥环弹性模量的增大呈现增大的趋势，这是由于随着水泥环弹性模量的增大，水泥环承担了更多的外部载荷，同时由于水泥环的刚度增大，其载荷传递系数增大，水泥环对作用在套管外壁的外部载荷起到的缓冲作用下降，使有一部分外部载荷与套管内壁压力相抵消，进而使套管受力降低；水泥环泊松比越大，套管应力也随之增大，这是由于水泥环泊松比变大，水泥环容易发生塑性变形，从而增大对套管外壁的挤压，同时水泥环越软，水泥环泊松比对套管应力影响越小。软硬地层不改变套管应力随水泥环弹性模量变化趋势，同时软硬地层对套管应力大小影响不大，这表明由于裂缝的存在，近裂缝段软硬地层是否承担更多的远场应力已影响较小，裂缝的诱导应力对套管应力起主要影响。

3.4 地应力场变化

全管柱不同部位的地应力场都有所差异，同时由于裂缝诱导应力的存在，近井筒地层原有地应力场发生改变，为此需要研究在裂缝诱导应力存在情况下，套管随着地应力场变化作用下承受的应力变化规律。

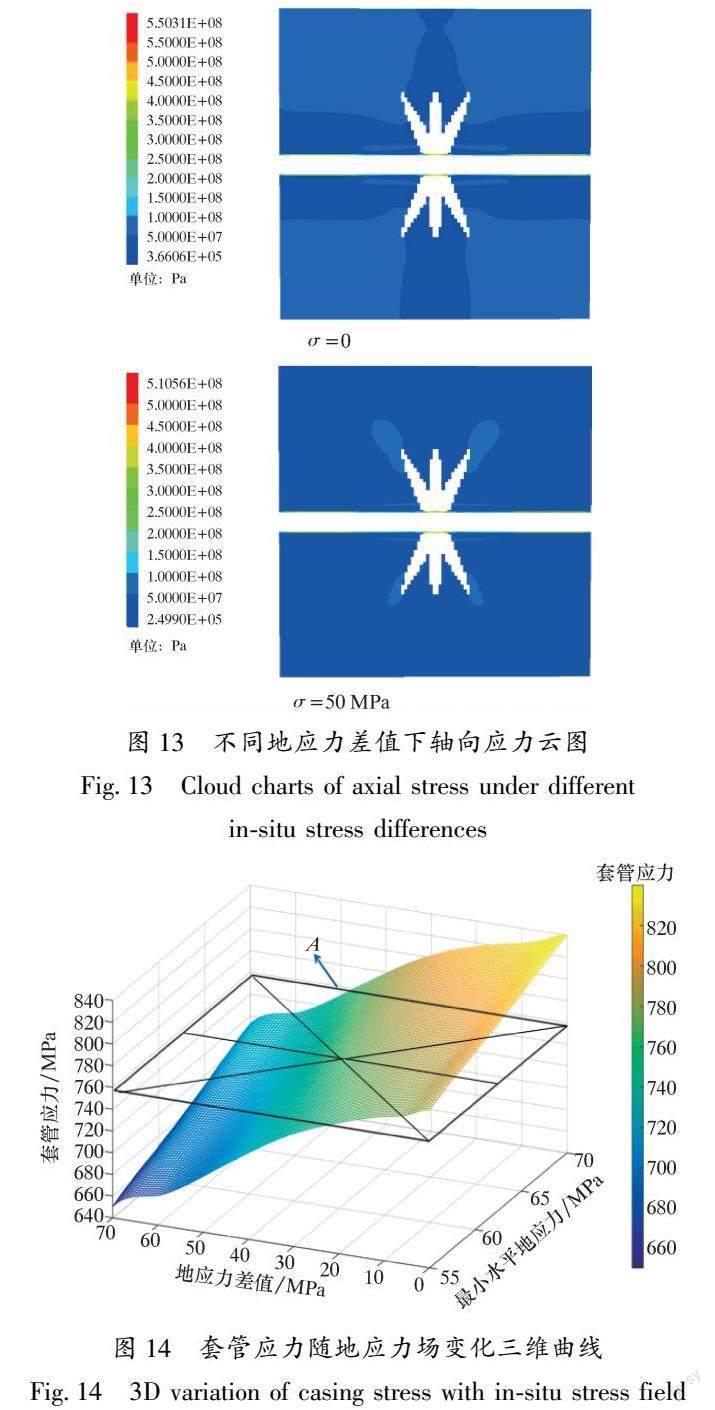
设置当最小水平主应力σmin变化范围为55～70 MPa且最大水平地应力σmax数值固定为60 MPa，垂向应力σh数值从60～130 MPa变化，地应力差σ（σ=σh-σmax）则为0～70 MPa。当σmin=65 MPa，σ=0和50 MPa时，模拟结果如图13所示；三维变化曲线如图14所示，其中A面为套管开始发生塑性变形面即套损面。

从图13可知，地应力差值较小时，轴向应力主要集中在压裂段套管内壁，随着地应力差值的增大，应力集中部位扩大到近裂缝段套管内壁，减弱了近井筒应力分布差异性。

从图14可以看出：套管在内壁压力70 MPa、地应力和裂缝诱导应力场作用下，随着地应力差值的增大，套管应力呈现减小的趋势，说明地应力差值的增大，有利于削弱裂缝诱导应力场附着于套管外载荷和套管内壁流体压力对套管壁面作用，从而起到保护套管的作用；当地应力差值一定时，套管应力随着最小水平地应力的增大而增大，这说明由于裂缝诱导应力的存在，近井筒周围应力场随着最小水平地应力的增大而得到增强，因此最小水平地应力对套管应力的影响不可忽略。整体来看，在地应力差值为21 MPa、最小水平地应力为55 MPa时，套管应力达到758 MPa，受力达到屈服极限；地应力差值为21 MPa、最小水平地应力为55 MPa、套管应力758 MPa的点位于三维坐标系套损面A面，若有其他点越过A面，此时套管压裂段发生塑性形变。因此，应根据三维图版选择合适地应力场对应的井段进行射孔压裂，从而降低套管损坏。

3.5 施工排量

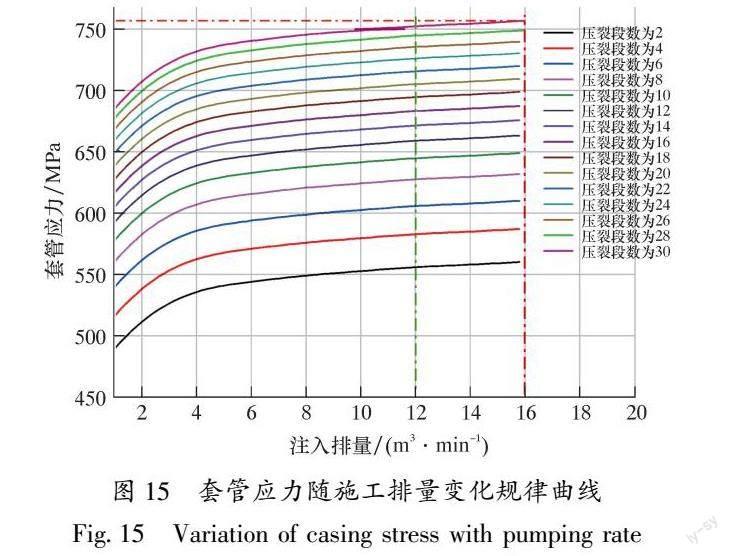
施工排量是压裂设计的关键参数，它影响施工泵压和裂缝的几何尺寸。压裂排量大小需要有利于携砂，又要控制裂缝高度的延伸。由于油田开发的需要，采用大排量压裂水平井的方式日益增多，非常容易造成套损。为研究施工排量对套管应力分布的影响，设置施工排量从1～16 m3/min变化，同时也考虑到实际现场施工存在多段压裂，为此设置压裂段数从2～30段变化。套管应力随施工排量变化规律曲线如图15所示。

从图15可知：随着排量增大套管所受应力增大，而受力增幅逐渐减少；随着压裂段数增加，由于累计效应导致的套管受力逐渐增加，同样其增幅逐渐减小，即变化趋势逐渐平缓。

当压裂施工段数为30段时，施工排量在12 m3/min以内，套管安全性很高；施工排量为16 m3/min时，套管达到屈服强度，此时套管存在一定安全风险。在该工况下只要固井质量良好且无地层错动现象，则套管仍然可以正常施工。考虑到套管的极限强度，根据现场实际压裂数据得知，极限排量要比屈服强度对应的施工排量大10%，此时对应的极限施工排量约为18 m3/min，套管发生严重变形，套管瞬间发生失稳变形，此时套管已经完全失效。

因此合理的施工排量建议在16 m3/min以内，极限的施工排量不得超过18 m3/min。

4 实例论证

以徐深气田芳深区块某井为例，压裂段存在诱导应力场情况下，分析套管应力分布情况。该井压裂段数为20段，选取某段射孔角为90°，压裂生成垂直裂缝；储层部位垂向应力70 MPa，最大主应力60 MPa，最小主应力55 MPa，根据现场数据得知井口施工压力最高可达到60 MPa，为此设置井底压力即套管内压为80 MPa，建立单缝-地层-套管-水泥坏三维有限元模型如图16所示；套管的应力分布云图如图17所示。

从计算结果可以看出，压裂段近井筒原地应力场由于裂缝诱导应力场的存在发生改变，套管在近井筒应力场作用和施工内压作用下，径向面套管应力集中部位位于压裂段内外壁面、周向应力集中于套管内壁的上部和下部、轴向应力则为压裂段内壁面；套管应力数值最大出现在周向面和轴向面，但由于射孔数仅有2孔，产生的裂缝诱导应力场对压裂段套管累计效应不大，使得套管应力未达到屈服强度，套管未发生塑性形变。

根据计算结果，在套管的压裂段位置尽量采用高强度材质套管，并配合使用良好的固井质量，可以降低套损的风险。

5 结论与建议

建立裂缝-地层-水泥环-套管有限元三维模型，通过理论公式验证模型可行性，从而进一步研究岩石弹性模量、套管内壁压力、水泥环弹性模量、地应力场变化和施工排量等对套管应力分布的影响，得到如下结论：

（1）当岩石弹性模量低于15 GPa时，套管发生塑性形变，而套管内壁无压力加剧了套管塑性变形程度；岩石弹性模量高于35 GPa且套管内壁无压力时，套管不易发生屈服破坏。

（2）套管应力随着套管内壁压力的增大而增大，而水泥环的软硬程度不影响套管应力变化趋势。

（3）套管应力随着水泥环弹性模量的增大呈现增大的趋势，套管应力随水泥环泊松比的增大而增大，软硬地层不改变套管应力随水泥环弹性模量变化趋势，同时软硬地层对套管应力大小影响不大。

（4）随着地应力差值的增大，套管应力呈现减小的趋势，当地应力差值一定时，套管应力随着最小水平地应力的增大而增大。

（5）随着排量增大套管所受应力增大，而受力增幅逐渐减少；随着压裂段数增加，套管应力变化趋势逐渐平缓。

（6）施工排量16 m3/min使得套管刚达到屈服强度值时，套管存在塑性变形，但变形程度小，到达极限施工排量18 m3/min时，套管已经完全失效。

［1］ 邹才能，翟光明，张光亚，等．全球常规-非常规油气形成分布、资源潜力及趋势预测［J］．石油勘探与开发，2015，42（1）：13-25．

ZOU C N，ZHAI G M，ZHANG G Y，et al.Formation，distribution，potential and prediction of global conventional and unconventional hydrocarbon resources［J］.Petroleum Exploration and Development，2015，42（1）：13-25.

［2］ 胡文瑞，翟光明，李景明．中国非常规油气的潜力和发展［J］．中国工程科学，2010，12（5）：25-29，63．

HU W R，ZHAI G M，LI J M.Potential and development of unconventional hydrocarbon resources in China［J］.Strategic Study of CAE，2010，12（5）：25-29，63.

［3］ 胡素云，赵文智，侯连华，等．中国陆相页岩油发展潜力与技术对策［J］．石油勘探与开发，2020，47（4）：819-828．

HU S Y，ZHAO W Z，HOU L H，et al.Development potential and technical strategy of continental shale oil in China［J］.Petroleum Exploration and Development，2020，47（4）：819-828.

［4］ 王坤，张烈辉，陈飞飞．页岩气藏中两条互相垂直裂缝井产能分析［J］．特種油气藏，2012，19（4）：130-133．

WANG K，ZHANG L H，CHEN F F.Productivity analysis for wells in shale gas reservoir with orthogonal fractures［J］.Special Oil & Gas Reservoirs，2012，19（4）：130-133.

［5］ L Z K，HE S L，GU D H，et al.Hydraulic Fracture Initiation while Staged Fracturing for Horizontal Wells［C］∥International Petroleum Technology Conference.Beijing，China：IPTC，2013：IPTC 16508-MS.

［6］ 郭天魁，张士诚，刘卫来，等．页岩储层射孔水平井分段压裂的起裂压力［J］．天然气工业，2013，33（12）：87-93．

GUO T K，ZHANG S C，LIU W L，et al.Initiation pressure of multistage fracking for perforated horizontal wells of shale gas reservoirs［J］.Natural Gas Industry，2013，33（12）：87-93.

［7］ 曾顺鹏，张国强，韩家新，等．多裂缝应力阴影效应模型及水平井分段压裂优化设计［J］．天然气工业，2015，35（3）：55-59．

ZENG S P，ZHANG G Q，HAN J X，et al.Model of multifracture stress shadow effect and optimization design for staged fracturing of horizontal wells［J］.Natural Gas Industry，2015，35（3）：55-59.

［8］ 尹建，郭建春，曾凡辉．水平井分段压裂射孔间距优化方法［J］．石油钻探技术，2012，40（5）：67-71．

YIN J，GUO J C，ZENG F H.Perforation spacing optimization for staged fracturing of horizontal well［J］.Petroleum Drilling Techniques，2012，40（5）：67-71.

［9］ DANESHY A A.Impact of offbalance fracturing on borehole stability and casing failure［C］∥SPE Western Regional Meeting.Irvine，California：SPE，2005：SPE 93620-MS.

［10］ LIAN Z H，YU H，LIN T J，et al.A study on casing deformation failure during multistage hydraulic fracturing for the stimulated reservoir volume of horizontal shale wells［J］.Journal of Natural Gas Science and Engineering，2015，23：538-546.

［11］ 于浩，练章华，徐晓玲，等．页岩气直井体积压裂过程套管失效的数值模拟［J］．石油机械，2015，43（3）：73-77．

YU H，LIAN Z H，XU X L，et al.Numerical simulation for casing failure during volumetric fracturing of shale gas vertical wells［J］.China Petroleum Machinery，2015，43（3）：73-77.

［12］ 于浩．体积压裂过程中套管失效机理研究［D］．成都：西南石油大学，2015．

YU H.Study on casing failure mechanism during volume fracturing［D］.Chengdu：Southwest Petroleum University，2015.

［13］ 于浩，练章华，林铁军，等．页岩气体积压裂过程中套管失效机理研究［J］．中国安全生产科学技术，2016，12（10）：37-43．

YU H，LIAN Z H，LIN T J，et al.Study on failure mechanism of casing in stimulated reservoir volume fracturing of shale gas［J］.Journal of Safety Science and Technology，2016，12（10）：37-43.

［14］ 高利军，乔磊，柳占立，等．页岩储层剪切套损的数值模拟及固井对策研究［J］．石油机械，2016，44（10）：6-10，16．

GAO L J，QIAO L，LIU Z L，et al.Numerical modeling and cementing countermeasure analysis of casing shear damage in shale reservoir［J］.China Petroleum Machinery，2016，44（10）：6-10，16.

［15］ 刘伟，陶长洲，万有余，等．致密油储层水平井体积压裂套管变形失效机理数值模拟研究［J］．石油科学通报，2017，2（4）：466-477．

LIU W，TAO C Z，WAN Y Y，et al.Numerical analysis of casing deformation during massive hydraulic fracturing of horizontal wells in a tightoil reservoir［J］.Petroleum Science Bulletin，2017，2（4）：466-477.

［16］ 杨钊，孙锐．致密气藏储层开发过程中套管应力分布影响规律研究［J］．能源与环保，2022，44（6）：1-9．

YANG Z，SUN R.Study on influence law of casing stress distribution in tight gas reservoir development［J］.China Energy and Environmental Protection，2022，44（6）：1-9.

［17］ SNEDDON I N.The distribution of stress in the neighbourhood of a crack in an elastic solid［J］.Proceedings of the Royal Society of London.Series A.Mathematical and Physical Sciences，1946，187（1009）：229-260.

［18］ SNEDDON I N，ELLIOT H A.The opening of a Griffith crack under internal pressure［J］.Quarterly of Applied Mathematics，1946，4（3）：262-267.

［19］ 李军，席岩．页岩气井筒完整性失效机理与控制方法［M］．北京：科学出版社，2020．

LI J，XI Y.Shale gas wellbore integrity failure mechanism and control method［M］.Beijing：Science Press，2020.

第一杨钊，教授，生于1978年，2010年毕业于东北石油大学油气田开发专业，获博士学位，现从事采油、采气工程理论研究与教学工作。地址：（163000）黑龙江省大庆市。电话：（0459）6503069。Email：954003199@qq.com。

通信作者：孫锐，Email：1553462374@qq.com。