PDC齿切削砂岩的细观损伤模拟

杨宏宇 邓嵘 叶柏良 何香江 黄安龙

摘要：在岩石切削过程中，刀具的切削参数对岩石的破坏方式和破岩效率有重要影响。为了研究PDC齿在不同切削参数下切削砂岩的细观损伤效果，采用离散单元法建立了PDC齿压入砂岩的数值模型，研究不同切削速度、前倾角及切削深度情况下，砂岩在PDC齿切削过程中的力场分布及裂纹发育情况的变化规律。研究结果表明：在一定范围内增加切削速度、前倾角和切削深度，剪切裂纹提前萌生且其占比增加；前倾角和切削速度对齿尖主裂纹的扩展影响较小，切削深度则对齿尖主裂纹的扩展影响较大；针对研究的砂岩，其临界切削深度为2 mm左右，当切削深度增加时，容易增加PDC齿齿尖产生的裂纹的长度，当裂纹长度达到5 mm及以上时，块体崩碎的频率提高，块体崩碎存在卸载现象。所得结论可为PDC齿的设计及切削参数的选择提供理论支持。

关键词：PDC齿；岩石切削；裂纹；细观损伤；离散元；数值模拟

0 引 言

在石油钻井、桥梁和隧道建设领域，常面临岩石切削相关问题，而在岩石切削过程中，刀具的切削参数对岩石的破坏方式和破岩效率有重要影响。揭示岩石的切削过程对优化破岩工具结构和最佳切削参数具有深远的意义［1］。关于离散单元法用于研究岩石切削的可行性在很多研究中得到证实［2-4］。LIU S.B.等［5］利用有限元软件分析了PDC齿不同冲击角β对破碎过程、力和机械比能的影响，结果表明，存在一个使破岩效率最高的冲击角β，它随冲击振幅、冲击力持续时间的增加而减小；况雨春等［6］提出一种PDC单齿切削力学计算模型，结合有限元数值模拟共同分析了PDC齿前倾角、侧倾角、齿径及切深与切削力的关系，二者结果一致，验证了该模型正确性；刘和兴等［7］利用有限元软件研究异形PDC齿切削花岗岩的破岩机理，并对不同种类异形PDC齿破岩过程进行对比分析，结果表明鞍形齿和双曲面齿破岩效率较高。还有学者［8-15］运用数值模拟方法分析了PDC齿前倾角、切削深度等切削参数与破岩效率的关系，结果表明，当切削深度达到临界切削深度时破碎比功较小，其他切削深度值的破碎比功均较大。

目前，关于PDC齿破岩研究主要存在以下2个问题：①大多未考虑裂纹的萌生和扩展、损伤演化、塑-脆性破坏等岩石细观损伤问题，主要在宏观层面进行分析；②PDC齿切削岩石分为塑性破坏和脆性破坏2种失效模式，但对于这2种失效模式的力场分布和裂纹扩展规律研究未见报道。

笔者基于离散元软件（PFC2D），建立了PDC齒切削砂岩的数值模型，研究PDC齿切削速度、前倾角及切削深度对砂岩裂纹占比、破碎方式的影响规律，并对不同切削速度、前倾角及切削深度等参数下的切削过程进行分析，得到PDC齿单齿受到的切削力、砂岩在PDC齿切削过程中的力场分布及裂纹发育情况的变化规律，并利用裂纹数对损伤程度进行评价。所得结论可为PDC齿的设计及切削参数的选择提供理论支持。

1 本构模型及参数标定

1.1 砂岩地层岩性

砂岩主要由各种碎片状石英、长石等矿石颗粒与黏土矿物这一最主要的填隙物质经压实胶结作用而成，故其与花岗岩、砾岩等差别较大，显示出较强烈的各向同性。砂岩的填隙物一般有2种：基质和胶结物。基质是指填充在碎屑颗粒之间的细小颗粒，主要是泥质矿物。胶结类物质具体指充填于碎片颗粒缝隙中的自生矿物质，最重要的类型有硅质、铁质和碳酸盐胶结物质。砂岩的微观结构如图1所示。

砂岩由众多矿物颗粒和填隙物胶结而成，实质上是一种众多颗粒组成的多孔隙固体材料。由于砂岩具有离散特性，使其在加载和卸载过程中表现出的力学性质具有一定随机性。离散元软件（PFC2D）是一种解决岩土工程问题的有效工具。笔者基于岩石细观力学特征，建立了圆盘颗粒运动和互作用模型。

1.2 接触模型的选择

离散元软件（PFC2D）主要使用的模型有线性模型（Linear）、接触黏结模型（Contact Bond）、平行黏结模型（Parallel Bond）、平节理模型（Flat-Jointed）4类。线性模型为散体模型，当接触黏结模型和平行黏结模型的黏结键断开后，退化后的模型为线性模型，这一本构关系更适合于砂土类材料；接触黏结模型和平行黏结模型统称黏结颗粒模型（BPM），都通过黏结键将颗粒黏结在一起，都可以承受压应力和剪应力。接触黏结为接触创造了一个线弹性力学状态，但黏结时仅在接触点处才有效；而平行黏结模型则可被看作在相互接触的颗粒间的交界处矩形区域有效，如图2所示。

二者区别在于前者只能传递力，后者可以传递力和力矩。平节理模型能够实现弹性和黏结（或摩擦滑动）的扩展界面宏观行为。平节理材料由通过平节理接触而连接的实体（单一颗粒、颗粒簇或墙体）组成。连接界面的力-位移响应是一种突发状态，包含从完全黏结状态到未完全黏结状态和摩擦状态。

在接触黏结中，只要颗粒之间还有接触，即使黏结键被破坏，模型接触性状仍是线弹性，类似于线性模型，颗粒刚度不会发生改变，这与岩石的力学特性不符。在平行黏结中，刚度由线弹性界面和线弹性黏结界面共同决定，黏结时能抵抗转动和剪切，并且可以传递力，而当载荷突破临界强度，平行黏结键在受载作用下断裂，导致无法传递载荷，模型刚度降低，这种现象符合砂岩的力学特性。因此本文选择平行黏结模型作为砂岩的接触模型。

区别于宏观层面的裂纹，PFC软件通过fish语言记录的裂纹是微观层面相邻颗粒间胶结断裂产生的裂纹，如图3所示。通过对微观裂纹发育情况分析，可以进一步了解宏观层面上岩石的损伤情况。

用PFC数值计算时需要调整砂岩模型微观参数，使其通过应力-应变曲线表征出的力学参数和试验真实力学参数在一个合理的误差范围内。岩石最重要的几个宏观参数分别是弹性模量E、泊松比μ、单轴抗压强度σc和抗拉强度σt。这些岩石的宏观参数将用来确定模型中颗粒的细观参数［11］。岩石的弹性模量E、泊松比μ、单轴抗压强度σc和抗拉强度σt这几个参数通过单轴压缩和巴西劈裂试验得出。单轴压缩试验岩样的直径和高度分别为50和100 mm。巴西劈裂试验用的岩样直径和高度分别为50和30 mm。在PFC2D中等尺寸建模，用于单轴压缩和巴西试验仿真的数值计算模型如图4所示。

1.3 接触模型选择

试验用砂岩岩心样品为青砂岩，取自四川隆昌。采用液压伺服驱动控制万能试验机完成岩石单轴压缩试验和巴西劈裂试验。砂岩岩样试验所得的应力-应变曲线如图5所示。

图5a是砂岩的单轴压缩参数标定的应力-应变曲线，可计算出砂岩的弹性模量、泊松比以及单轴抗压强度；图5b是砂岩的巴西劈裂试验参数标定的应力-应变曲线，可计算出砂岩的抗拉强度。砂岩宏观参数分别为：弹性模量E=2.799 GPa，泊松比μ=0.22，抗压强度σc=25.72 MPa，抗拉强度σt=1.64 MPa。

在PFC2D软件中，模型的细观参数需根据岩石力学试验应力-应变结果和破坏形式确定［16-18］。将数值计算模型在PFC2D软件中进行单轴压缩和巴西劈裂模拟，对比试验结果，采用“试错法”［19］往复调整砂岩模型微观参数，使其通过应力-应变曲线表征出的力学参数相比试验真实力学参数误差缩小，最终确定模型的微观参数。选用经标定后的微观参数能够较好地表征砂岩岩样的力学特性。试验与模拟的应力-应变曲线如图5所示。

本文所选砂岩细观参数分别为：颗粒密度ρ=2 700 kg/m3，接触和黏结部分的弹性模量E=5.857 GPa，法向强度ρ—c=12.05 MPa，摩擦角Φ=22°，摩擦因数f=0.57，接触和黏结部分的刚度比k=1.5，切向强度τ—c=12.05 MPa。

1.4 接触模型的选择

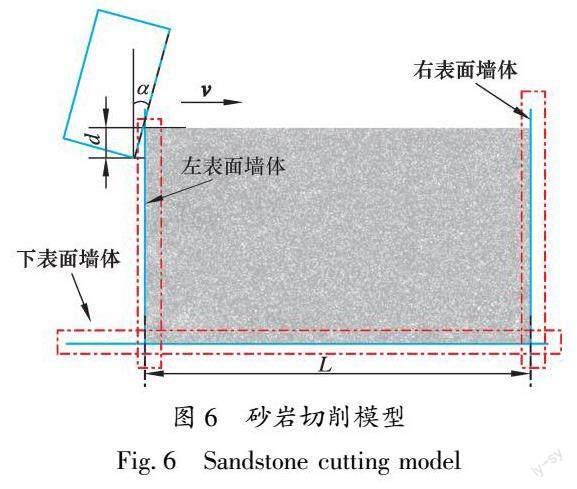
二维砂岩切削模型如图6所示。模型的长L和高H分别为100和50 mm，包含了30 228个半径为0.15～0.30 mm的颗粒。采用颗粒逐步膨胀法生成砂岩模型。颗粒簇的右以及下表面用刚性墙体来约束岩石模型的自由度。切削刀具以选定的速度v和前倾角α沿着水平方向切削砂岩20 mm，切削深度为d。

2 切削参数对损伤程度及裂纹扩展的影响

在本文数值模拟中，研究PDC齿的切削速度、切削深度以及前倾角对岩石损伤程度的影响情况。具体模拟方案如表1所示。

2.1 切削速度

研究表明，PDC齿切削岩石的过程满足密实核理论相关准则［20］。PDC齿切削砂岩示意图如图7所示，该过程是局部压入岩石的过程，从齿尖处形成核心挤压区、塑性影响区和弹性影响区。塑性影响区是以齿尖与岩石接触点为原点的半球壳区域和核心挤压区外侧，弹性影响区是以齿尖与岩石接触点为原点的半球壳区域和塑性影响区外侧。

砂岩在PDC齿以0.3和1.0 m/s的速度切削时破碎情况和力场分布如图8所示。从图8a可看出，当切削速度较小时，增加切削速度，砂岩逐渐由塑性破坏过渡为脆性破坏，发生块体崩碎。从图8b可以看出，在离散元软件PFC2D中，接触力大小可以通过其力链颜色或粗细判断，例如接触力最大的区域呈现红色且线条最粗，接触力最小的区域呈现蓝色且线条最细。接触力集中于PDC齿前方，PDC齿齿尖压力最大，且随着切削速度增加，PDC齿前方压力作用区域扩大，其他区域的压力力场分布更分散。

图8表明，在一定范围内提高切削速度，会扩大砂岩的力场范围和PDC齿前方压力，有利于在齿尖周围的砂岩形成密实核，微裂纹进一步发展并贯通到砂岩自由面，进而产生块体崩碎。

在PFC软件中，裂纹总数指拉伸裂纹数和剪切裂纹数的总和，裂纹占比指单一种类裂纹占总裂纹数的百分比。以0.3、0.6和1.0 m/s速度切削砂岩时，裂纹占比、裂纹总数随切削速度变化情况如图9所示。由图9可见，切削速度影响剪切裂纹萌生，当切削速度增加时总裂纹数也会不断增加，剪切裂纹会提前萌生且占比增加，但仍然是以拉伸裂纹为主。

2.2 前倾角

砂岩在PDC齿以5°、10°和15°前倾角下破碎情况和力场分布如图10所示。

从图10a可看出，增加PDC齿前倾角，砂岩逐渐由塑性破坏过渡为脆性破坏，PDC齿前方的砂岩压碎区域扩大，并且发生块体崩碎。从图10b可看出，当PDC齿倾角增大时，PDC齿前方接触力集中于砂岩自由面，有利于产生块体崩碎；由于齿尖压力较集中，在压力梯度较大的区域容易萌生长裂纹，且随着PDC齿前倾角增加，对PDC齿前方压力作用的区域大小影响较小，表明一定范围内增加前倾角，会改变PDC齿前方压力集中区域，有利于微裂纹发展至贯穿到砂岩自由面，进而产生块体崩碎。

不同前倾角PDC齿切削砂岩的裂纹数变化曲线如图11所示。

由图11a可知，当前倾角增加时，总裂纹数也不断增加，但当前倾角从10°增加至15°时，裂纹数变化不明显，因此针对选定砂岩，PDC齿前倾角在10°～15°范圍内优选，单位时间内裂纹数较多，对岩石的损伤也更大。由图11b可知：PDC齿不同前倾角切削砂岩，产生的拉伸和剪切2种类型的裂纹占比会发生变化；剪切裂纹萌生更早且裂纹占比增加；相比于切削速度，前倾角对剪切裂纹萌生影响更大。

2.3 切削深度

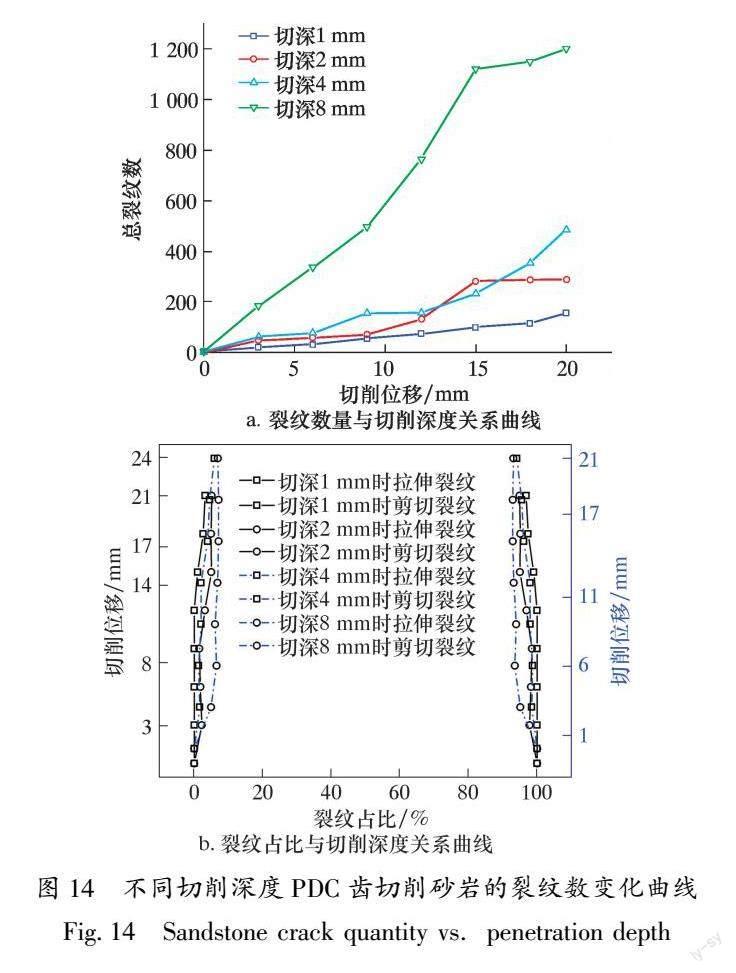
砂岩在PDC齿以1、2、4和8 mm深度切削时的破碎情况如图12所示。从图12a和图12b可以看出：当切削深度为1 mm时，砂岩微裂隙处于稳态发展阶段，颗粒状岩屑在PDC齿前齿面不断堆积，砂岩以塑性破坏为主；当切削深度增加至2 mm，PDC齿前端密实核区域增大，由齿尖产生约5 mm长度的裂纹，增加切削深度，砂岩逐渐由塑性破坏过渡为脆性破坏，发生块体崩碎。从图12c和图12d可以看出：当切削深度为4 mm时，PDC齿前端密实核区域继续增大，齿尖产生的裂纹长度增加至9 mm，相比于切深2 mm块体崩碎的岩屑体积增大了1倍；当切削深度为8 mm时，PDC齿前端密实核区域继续增大，在PDC齿前方萌生了1条裂纹，其与齿尖产生的裂纹交汇成1条长度近20 mm的新裂纹，块体崩碎的大块砂岩岩屑会发生二次破碎，这种二次破碎机制特点是岩石被压碎并破碎成颗粒大小的小块。针对研究的砂岩，其临界切削深度为2 mm左右，当达到临界切削深度，砂岩逐渐由塑性破坏过渡为脆性破坏，发生块体崩碎。随着切削深度增加，较容易增加PDC齿齿尖产生的裂纹的长度，提高块体崩碎的频率，砂岩破碎方式由塑性破坏转向脆性破坏。

砂岩在PDC齿以1、2、4和8 mm深度切削时的力场分布如图13所示。从图13a和图12b可以看出，接触力集中于PDC齿前方，PDC齿齿尖压力最大，且随着切削速度增加，PDC齿前方压力作用区域扩大，PDC齿前方压力作用区域扩大，其他区域压力力场分布更分散，表明增加切削深度，PDC齿与砂岩接触面增加，总切削力也随着增加，会增加砂岩的力场范围和PDC齿前方压力。从图13c和图13d可以看出，PDC齿产生块体崩碎后，会存在卸载现象，崩碎的大体积岩屑没有接触力力场分布，说明该区域不受力，因此当岩石脆性破坏时，崩碎的岩石体积达到一定程度，会显著影响块体崩碎后切削力的大小。

圖14a是切削砂岩裂纹数量与切削深度的关系曲线。图14b是切削砂岩的剪切裂纹和拉伸裂纹与切削深度的关系曲线。

从图14a可以看出，PDC齿不同切削深度切削砂岩，会影响拉伸和剪切2种类型的裂纹占比。当切削深度成倍增加时，总裂纹数也成倍增加，同时提高了对砂岩块体崩碎的频率，相较于前倾角，切削深度对裂纹占比影响较小。从图14b可以看出，PDC齿以1 mm切削深度切削砂岩时，在12 mm切削长度以内未产生剪切裂纹，此后缓慢增加，在20 mm切削长度时，剪切裂纹占总裂纹数的3%；PDC齿分别以2、4和8 mm切削深度切削砂岩时，初始破碎就能产生剪切裂纹，剪切裂纹占比逐步增长，此后趋于稳定。因此，增加切削深度，会使砂岩的剪切裂纹更快萌生且其剪切裂纹占比显著增加。

3 结 论

本文为研究PDC齿切削参数对砂岩细观损伤的影响，利用离散元软件（PFC2D）建立了PDC齿切削砂岩的数值模型。通过单轴压缩和巴西劈裂试验确定岩石的宏观力学参数，利用“试错法”确定了颗粒微观参数，提出了裂纹占比的概念，研究了PDC齿切削速度、前倾角及切削深度对砂岩裂纹占比、破碎方式的影响规律，并对不同切削速度、前倾角及切削深度等参数下的切削过程进行分析研究，得到了PDC齿单齿受到的切削力，砂岩在PDC齿切削过程中的力场分布及裂纹发育情况的变化规律，并利用裂纹数对损伤程度进行评价。研究结果为：

（1）当切削速度在1 m/s范围内增加，会增加砂岩的力场范围和PDC齿前方压力，切削深度影响增大有利于齿尖附近砂岩形成密实核，总裂纹数也会不断增加，剪切裂纹会提前萌生且其占比增加，加深了PDC齿对岩石的损伤程度，也会使平均切削力增大，但切削速度对齿尖裂纹发育影响较小。

（2）增加PDC齿前倾角对齿尖裂纹发育影响较小，但会使砂岩逐渐由塑性破坏过渡为脆性破坏，PDC齿前方的砂岩压碎区域扩大，进而发生块体崩碎。前倾角增加，总裂纹数也增加，剪切裂纹会提前萌生且其裂纹占比增加，相比于切削速度，前倾角对剪切裂纹萌生影响更大，会加深PDC齿对岩石的损伤程度，也会使平均切削力增大。

（3）针对研究的砂岩，其临界切削深度为2 mm左右，当达到临界切削深度时，砂岩逐渐由塑性破坏过渡为脆性破坏，发生块体崩碎。当切削深度增加时，齿尖产生的裂纹长度也增加，当裂纹长度达到5 mm时，块体崩碎的频率提高；另一方面，剪切裂纹占比越大，会使砂岩的剪切裂纹更快萌生且其剪切裂纹占比显著增加。

（4）砂岩块体崩碎存在卸载现象，崩碎的大体积岩屑不受力，因此当岩石脆性破坏时，崩碎的岩石体积达到一定程度，会显著影响块体崩碎后切削力的大小。

参考文献：

［1］MENEZES P L，LOVELL M R，AVDEEV I V，et al.Studies on the formation of discontinuous chips during rock cutting using an explicit finite element model［J］.The International Journal of Advanced Manufacturing Technology，2014，70（1）： 635-648.

［2］HUANG H，LECAMPION B，DETOURNAY E.Discrete element modeling of tool-rock interaction I： rock cutting［J］.International Journal for Numerical and Analytical Methods in Geomechanics，2013，37（13）： 1913-1929.

［3］刘伟吉．井底岩石塑脆性破碎机理及其影响因素研究［D］．成都：西南石油大学，2017．

LIU W J.The ductile-brittle failure mechanism and its influence factors investigation of bottom hole rock［D］.Chengdu： Southwest Petroleum University，2017.

［4］刘彪，吴杰，张俊，等．基于离散元方法的PDC钻头切削齿破岩机理数值模拟［J］．矿业研究与开发，2021，41（2）：165-169．

LIU B，WU J，ZHANG J，et al.Numerical simulation on the rock breaking of cutter teeth of PDC cutter based on discrete element method［J］.Mining Research and Development，2021，41（2）： 165-169.

［5］LIU S B，NI H J，ZHANG H，et al.Numerical study on optimal impact angle of a single PDC cutter in impact rock cutting［J］.Energy Reports，2021，7： 4172-4183.

［6］况雨春，张明明，冯明，等．PDC齿破岩仿真模型与全钻头实验研究［J］．地下空间与工程学报，2018，14（5）：1218-1225．

KUANG Y C，ZHANG M M，FENG M，et al.Simulation model of PDC tooth cutting rock and experimental research on the bit［J］.Chinese Journal of Underground Space and Engineering，2018，14（5）： 1218-1225.

［7］刘和興，罗云旭，刘伟吉，等．异形PDC齿切削破碎非均质花岗岩机理研究［J］．石油机械，2022，50（4）：22-31．

LIU H X，LUO Y X，LIU W J，et al.Rock-breaking mechanism of special-shaped PDC cutter in heterogeneous granite［J］.China Petroleum Machinery，2022，50（4）： 22-31.

［8］祝效华，李海．PDC切削齿破岩效率数值模拟研究［J］．应用基础与工程科学学报，2015，23（1）：182-191．

ZHU X H，LI H.Numerical simulation on mechanical special energy of PDC cutter rock-cutting［J］.Journal of Basic Science and Engineering，2015，23（1）： 182-191.

［9］李其州，张凯，周琴，等．切削深度对PDC齿超高速破岩机理的影响分析［J］．石油机械，2022，50（6）：1-8．

LI Q Z，ZHANG K，ZHOU Q，et al.Influence of cutting depth on rock breaking mechanism of PDC cutter at ultra-high speed［J］.China Petroleum Machinery，2022，50（6）： 1-8.

［10］孟凡海．基于离散元的PDC齿冲击破岩规律研究［D］．大庆：东北石油大学，2020．

MENG F H.Research on rock breaking law of PDC teeth impact based on discrete element［D］.Daqing： Northeast Petroleum University，2020.

［11］MOHAMMADNEJAD M，DEHKHODA S，FUKUDA D，et al.GPGPU-parallelised hybrid finite-discrete element modelling of rock chipping and fragmentation process in mechanical cutting［J］.Journal of Rock Mechanics and Geotechnical Engineering，2020，12（2）： 310-325.

［12］CHENG Z，LI G S，HUANG Z W，et al.Analytical modelling of rock cutting force and failure surface in linear cutting test by single PDC cutter［J］.Journal of Petroleum Science and Engineering，2019，177： 306-316.

［13］DENG R，GUO E，CHEN K，et al.Study on damage law of rock by Pdc cutter cutting［J］.International Core Journal of Engineering，2019，5（11）： 145-153.

［14］CHE D M，ZHANG W Z，EHMANN K.Chip formation and force responses in linear rock cutting： an experimental study［J］.Journal of Manufacturing Science and Engineering，2017，139（1）： 011011.

［15］SHENG M，CHENG Z，GAO S Y，et al.Shale bedding planes control rock removal behaviors of PDC cutter： single cutter experiment［J］.Journal of Petroleum Science and Engineering，2020，185： 106640.

［16］LIU Y Y，ZHANG X W，SHI J F，et al.A reservoir quality evaluation approach for tight sandstone reservoirs based on the gray correlation algorithm： a case study of the Chang 6 layer in the W area of the as oilfield，Ordos Basin［J］.Energy Exploration & Exploitation，2021，39（4）： 1027-1056.

［17］GHAZVINIAN E，DIEDERICHS M S，QUEY R.3D random Voronoi grain-based models for simulation of brittle rock damage and fabric-guided micro-fracturing［J］.Journal of Rock Mechanics and Geotechnical Engineering，2014，6（6）： 506-521.

［18］李靜，孔祥超，宋明水，等．储层岩石微观孔隙结构对岩石力学特性及裂缝扩展影响研究［J］．岩土力学，2019，40（11）：4149-4156．

LI J，KONG X C，SONG M S，et al.Study on the influence of reservoir rock micro-pore structure on rock mechanical properties and crack propagation［J］.Rock and Soil Mechanics，2019，40（11）： 4149-4156.

［19］田文岭，杨圣奇，黄彦华．卸围压下砂岩力学特性及细观机制颗粒流分析［J］．岩土力学，2016，37（增刊2）：775-782．

TIAN W L，YANG S Q，HUANG Y H.Particle flow analysis of mechanical behavior and meso-mechanism of sandstone under unloading confining pressure［J］.Rock and Soil Mechanics，2016，37（S2）： 775-782.

［20］LIU H Y，KOU S Q，LINDQVIST P A，et al.Numerical simulation of the rock fragmentation process induced by indenters［J］.International Journal of Rock Mechanics and Mining Sciences，2002，39（4）： 491-505.