无公共边的双圈图上置信传播算法的收敛性和正确性*

靳艺香,杨卫华

(太原理工大学 数学学院,山西 晋中 030600)

0 引言

置信传播(Belief Propagation)算法是一种在因子图上描述的消息传递算法,1982年由Pearl[1]提出后广泛应用在数字通信、人工智能、计算机科学、运筹管理等领域.1988年Pearl[2]证明了置信传播算法在树上收敛且收敛到正确先验概率.2000年Weiss[3]提出单圈上的置信传播算法(置信更新算法)在单圈图中收敛,且当变量为二元时纠正置信收敛到正确边际.Cantwell和Newman[4]给出了置信传播算法在一类特殊多全图上的收敛性与正确性.但置信传播算法在多圈图上的传播收敛性与正确性尚未建立有效方法,而其在多圈图上的收敛性与正确性在通信的译码领域扮演着重要的理论角色[5].因此,本文研究置信传播算法在无公共边的双圈图(网络)上的收敛性和正确性,并进行仿真分析.

1 置信传播算法

1.1 置信传播算法基础

为了使用置信传播算法,在马尔可夫随机场中定义了两个概念: 消息和置信.设是节点X发送给节点Y 的消息.定义图中边的传递矩阵[2]为

1.2 单圈图的置信传播算法[3]

1.2.1 单圈

2000年Weiss给出了单圈上的置信传播算法[3].考虑一个由N个未观测节点和N个观测节点组成的单圈(即一个圈),每个未观测节点上有一个观测节点(见图1(a)).我们用U1,···,UN表示单圈中的未观测节点(白色圈),用O1,···,ON表示相应的观测节点(黑色圈).Oi称为Ui的局部证据,定义对角矩阵Di的对角线元素为Oi传递给Ui的消息向量(i1,2,···,N),称Di为局部证据概率矩阵.

由此可知,置信传播算法在单圈收敛.

当消息向量为二元时,利用传递矩阵的特征值纠正置信.设传递矩阵CN1的主特征值为λ1,次特征值为λ2.则节点U1的纠正置信向量为

1.2.2 单圈和附加树

将上部分内容扩展到带附加树的单圈上[3](见图1(b)).对于圈内节点: 在有限次迭代后,非圈内节点传入圈中的消息收敛为稳态值视为局部证据,所以圈内节点置信收敛且(二元时)纠正置信正确.对于非圈内节点置信收敛,二元时纠正置信仍可能不正确.

本文使用Weiss[3,6－7]的术语,研究无公共边的双圈图(分为无公共边的双圈和带附加树的无公共边的双圈)中置信传播的收敛性和正确性.

2 无公共边的双圈的置信传播算法

2.1 无公共边的双圈的分类

对带有局部证据的无公共边的双圈按两圈间的距离可分为3类: 相邻的双圈,两圈距离为1的双圈和两圈距离大于1的双圈.

相邻的双圈:两圈有一个公共点,见图2(a).

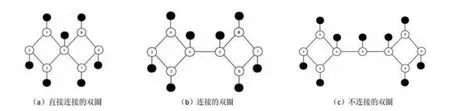
图2 双圈图分类

两圈距离为1的双圈:两圈距离为1,即双圈是由两圈距离为1的一条边连接,见图2(b).

两圈距离大于1的双圈:两圈距离大于等于2,即双圈之间可以有大于1个节点连接的双圈,见图2(c).

2.2 相邻的双圈置信传播算法

考虑一个由N1+N2-1个未观测节点和N1+N2-1个观测节点组成的相邻的双圈(见图2(a)).我们用A1,···,表示左圈中的未观测节点,用OA1,···,表示相应的观测节点;用B1,···,表示右圈中的未观测节点,用OB1,···表示相应的观测节点.两圈由公共节点相连.见图3(a).

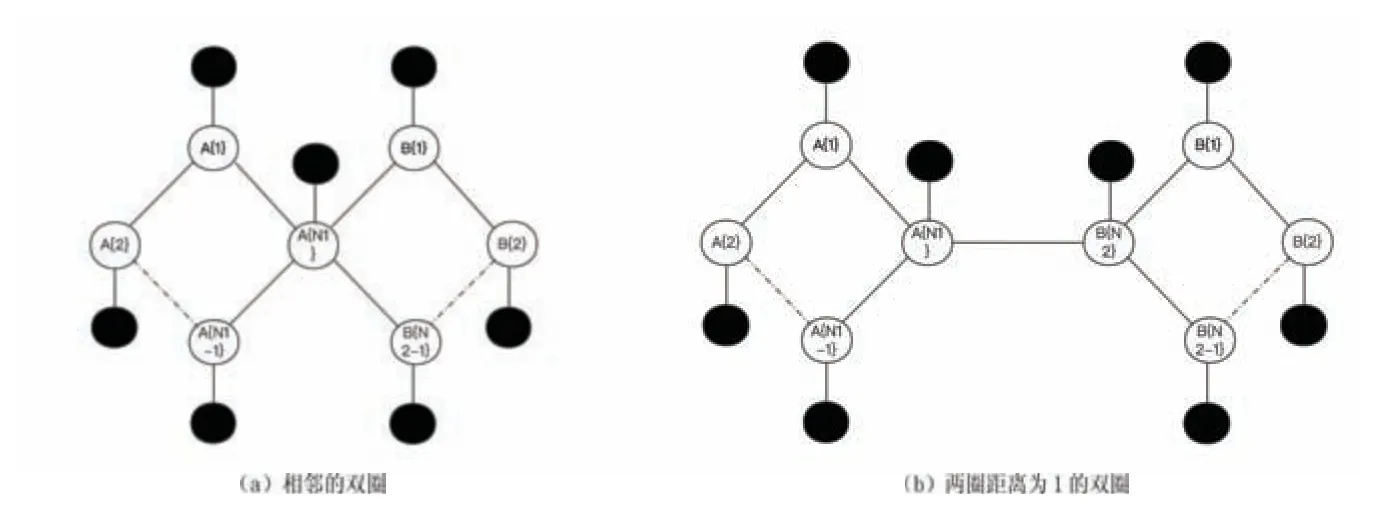
图3 相邻的双圈变为两圈距离为1的双圈

将相邻的双圈变为两圈距离为1的双圈的方法:

从而利用两圈距离为1的双圈的置信传播算法规则解决相邻的双圈问题.

2.3 两圈距离为1的双圈置信传播算法

考虑一个由N1+N2个未观测节点和N1+N2个观测节点组成的两圈距离为1的双圈(见图3(b)).A1,···,表示左圈中的未观测节点,B1,···,表示右圈中的未观测节点.两圈之间由间的一条边相连.

2.3.1 初始消息设置

2.3.2 第n次迭代时的消息传递

1）右圈看作左圈的局部证据

由消息传递规则可知:

由此,将原来的双圈网络变为单圈网络.

2）左圈网络的迭代收敛

现求左圈各节点置信

当左圈迭代到稳态时该置信称为稳态置信.

3）稳态的左圈看作右圈的局部证据

使得双圈网络变为单圈网络.

与左圈迭代相似,类比式(9)和式(10)有

4）稳态的右圈看作左圈的局部证据

2.4 两圈距离大于1的双圈置信传播算法

2.4.1 初始消息设置

2.4.2 第n次迭代时的消息传递

1）右圈看作左圈的局部证据

由此,将原来的双圈变为单圈.

2）左圈网络的迭代收敛

两圈距离大于1的双圈图中左圈的迭代收敛与2.3.2节中2)左圈网络的迭代收敛相同,此处不再赘述.

3）稳态的左圈看作右圈的局部证据

由此双圈变为单圈.右圈中各节点置信与式(18)相同.

4）稳态的右圈看作左圈的局部证据

由式(21)和式(22)可知:

重复2.4.2节2)～4)部分的公式,直至各消息收敛.

3 无公共边的二元双圈的纠正置信传播算法

利用Weiss[3]对二元单圈（单圈中各节点变量为二元）的纠正置信传播算法,对无公共边的二元双圈（双圈中各节点变量为二元）置信传播算法中涉及单圈的部分进行纠正.

3.1 相邻的二元双圈纠正置信传播算法

与2.2节相同,将相邻的双圈转变为两圈距离为1的双圈,利用两圈距离为1的双圈的纠正置信传播算法解决相邻的双圈问题.

3.2 两圈距离为1的二元双圈纠正置信传播算法

设两圈距离为1的双圈中变量均为二元.两圈距离为1的二元双圈的纠正置信传播算法仅对2.3.2节中以下部分进行改变,其余不变.

3.3 两圈距离大于1的二元双圈纠正置信传播算法

两圈距离大于1的双圈的纠正置信传播算法,在其置信传播算法的基础上作出以下改变:

1）在2.4.2节2)后加入式(27).

2）将式(23)改为

3）在2.4.2节3)后加入式(29).

4）将式(25)改为

4 无公共边的双圈的收敛性与正确性

4.1 无公共边的双圈的收敛条件

定理1若无公共边的双圈网络中任一消息有(n为迭代次数),则其全局收敛.

证明置信传播算法和纠正置信传播算法仅对置信进行运算,不影响消息的收敛.因此本文仅对无公共边的双圈的置信传播算法进行分析.

本文仅对两圈距离为1的双圈进行证明,相邻或两圈距离大于1的双圈证明类似,不予赘述.

对于两圈距离为1的双圈:

4.2 双圈的收敛性实验

相邻的双圈实验结果与两圈距离为1的双圈相同,仅展示两圈距离为1的双圈结果.

4.2.1 两圈距离为1的双圈

图4(a)显示了一个由8个未观测节点和8个观测节点组成的连接的双圈图网络,图4(b)显示了各观测节点处于状态1或状态2时的局部证据概率.设传递矩阵为:

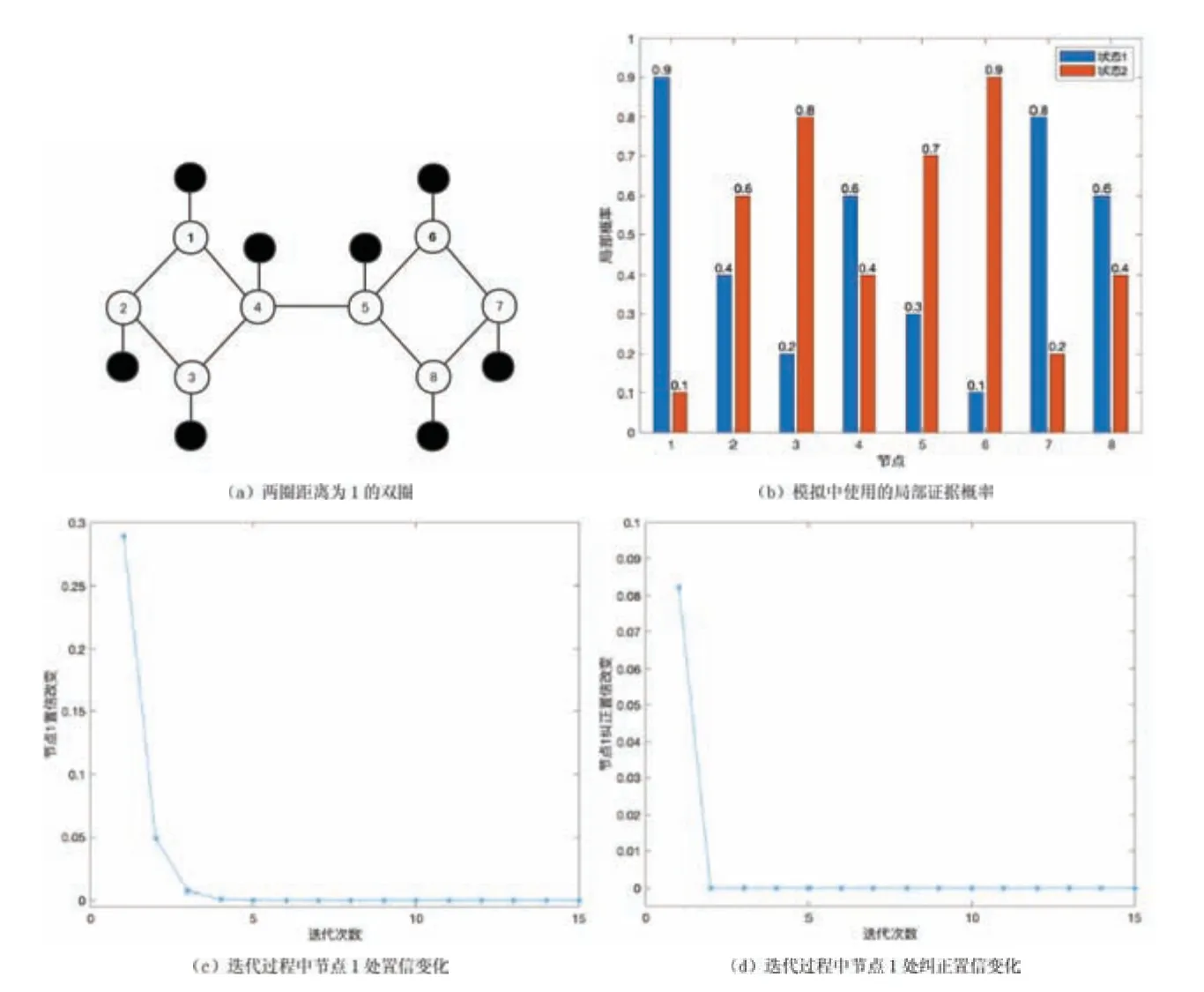
图4 两圈距离为1的双圈收敛实验结果

图4(c～d)显示了节点1的置信收敛速度和纠正置信收敛速度,可以看到纠正置信收敛速度较快.

图5(b)显示了正确的边际值(通过穷举枚举计算),由图5(c～d)知置信配置与正确边际配置不同;纠正置信配置与正确边际配置相同,且纠正置信概率值均与正确边际值相同(配置: 某节点概率最大的状态).

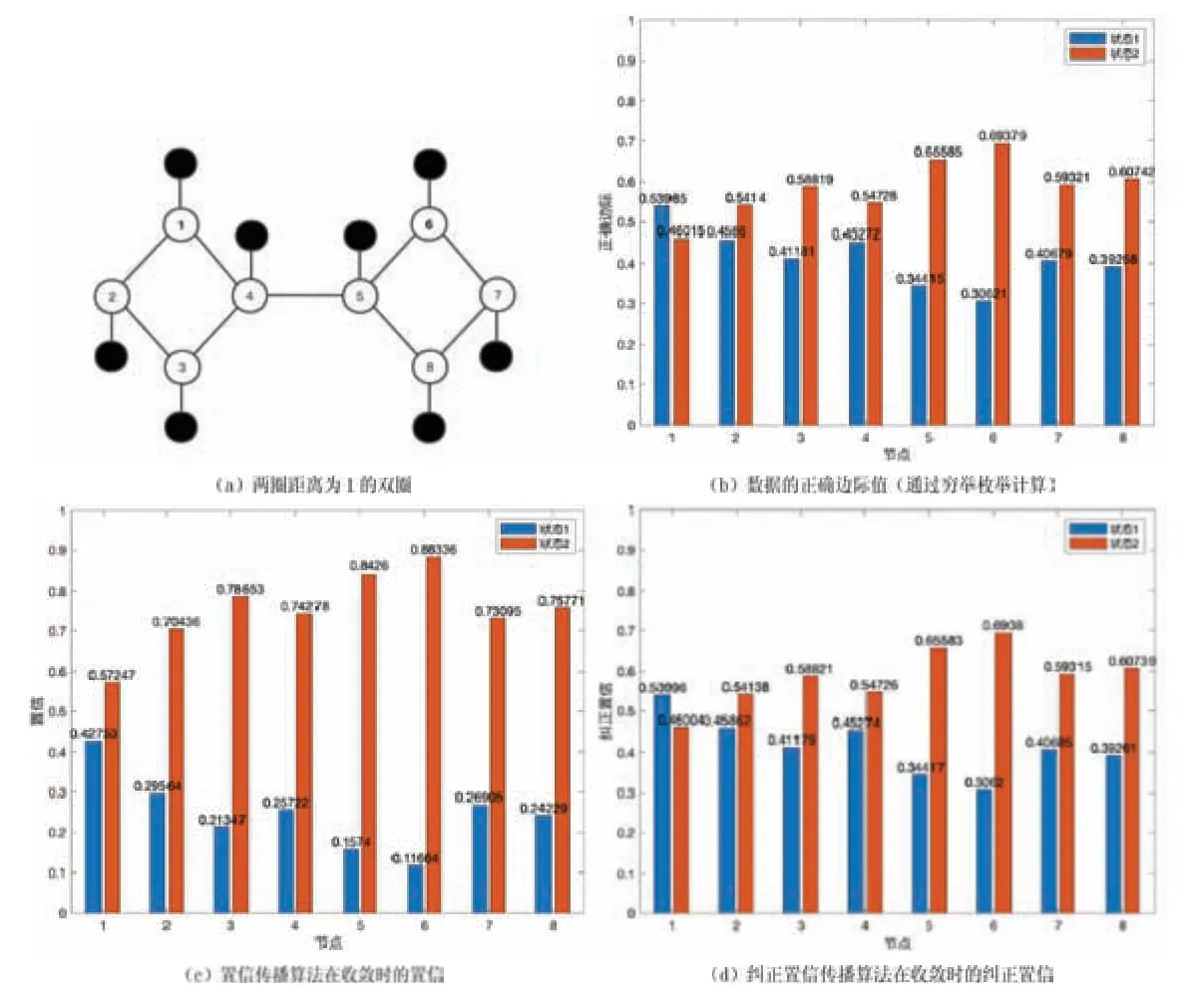
图5 两圈距离为1的双圈收敛实验结果

用二阶随机矩阵定义图5(a)中边的过渡矩阵及各节点的局部证据概率矩阵.分别用置信传播算法和纠正置信传播算法对该图进行仿真分析,各进行5 000次仿真实验,由表1知两圈距离为1的二元双圈100%收敛.

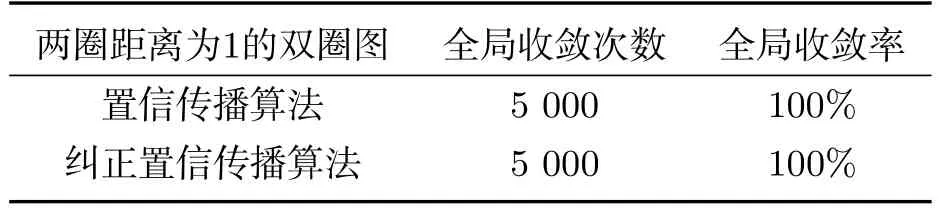
表1 进行5 000次仿真，两圈距离为1的双圈的全局收敛率

4.2.2 两圈距离大于1的双圈

图6(a)显示了一个由9个未观测节点和9个观测节点组成的两圈距离大于1的双圈.设过渡矩阵不变,利用其置信传播算法和纠正置信传播算法对该图进行仿真实验.由实验结果(图7)可知,置信配置与正确边际配置不同;纠正置信配置与正确边际配置相同,且纠正置信概率值均与正确边际值相同.

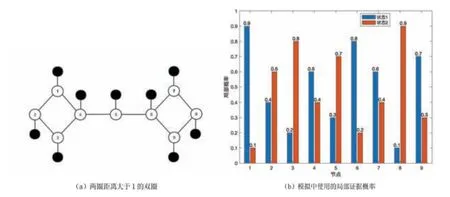
图6 两圈距离大于1的双圈收敛实验结果

图7 两圈距离大于1的双圈实验结果

利用两种算法进行5 000次仿真实验,仿真结果见表2,可知两圈距离大于1的双圈100%收敛,由此可以看出研究双圈全局收敛是有意义的,且定理1是有意义的.

表2 进行5 000次仿真，两圈距离大于1的双圈的全局收敛率

4.3 无公共边的双圈的正确性实验

利用无公共边的双圈的置信传播算法和纠正置信传播算法对各类二元双圈进行5 000次仿真实验(表3),观察全局收敛时稳态置信与正确边际配置相同的次数,并计算各自的正确率.由表3可知,对于无公共边的二元双圈,纠正置信传播算法的正确率为100%,大于置信传播算法.

表3 无公共边的二元双圈的正确性

5 带附加树的无公共边双圈的收敛性与正确性

将上节内容扩展到无公共边的双圈和附加树上,研究各类带附加树的无公共边双圈中置信传播的收敛性和正确性.

5.1 相邻的双圈与附加树分类

无附加树的相邻的双圈图见图8(a),带附加树的相邻的双圈图可分为两类: 附加树在圈上且不在两圈公共点上(见图8(b));附加树在两圈公共点上(见图8(c)).

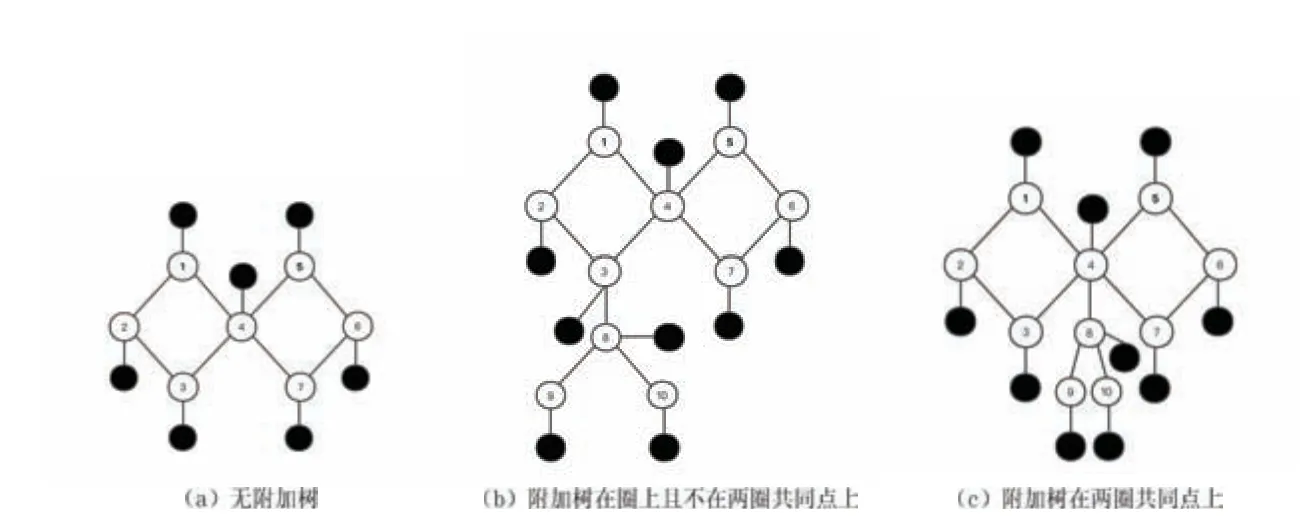
图8 相邻的双圈与附加树

5.2 两圈距离为1的双圈与附加树分类

无附加树的两圈距离为1的双圈图见图9(a),带附加树的两圈距离为1的双圈图可分为两类: 附加树在圈上且不在两圈连接线上(见图9(b));附加树在圈上且在两圈连接线上(见图9(c)).

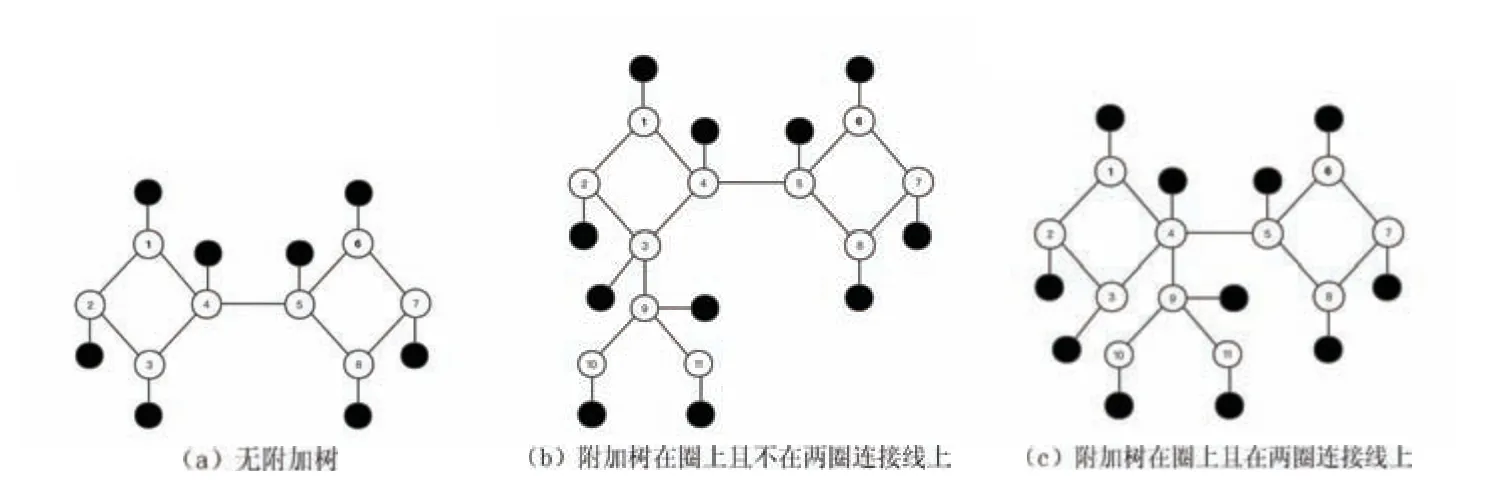
图9 两圈距离为1的双圈与附加树

5.3 两圈距离大于1的双圈与附加树分类

无附加树的两圈距离大于1的双圈图见图10(a);带附加树的两圈距离大于1的双圈图可分为三类: 附加树在圈上且不在两圈连接线上(见图10(b));附加树在圈上且在两圈连接线上(见图10(c));附加树不在圈上且在两圈连接线上(见图10(d)).

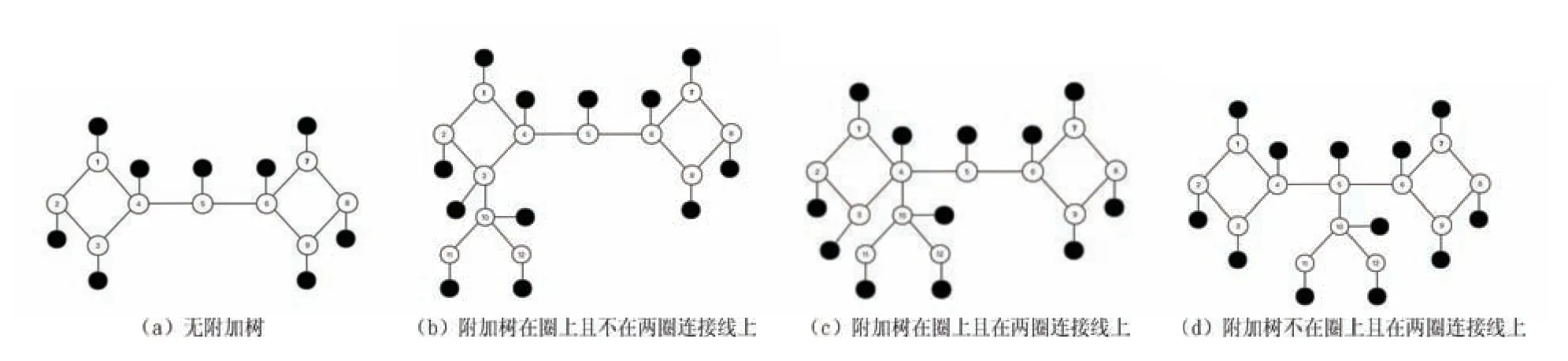
图10 两圈距离大于1的双圈与附加树

5.4 实验

对于相邻的双圈,若附加树在非共同节点上,利用2.2节转换为两圈距离为1的双圈进行实验;若附加树在两圈共同节点上,将附加树看作观测节点,复制后实验.由此相邻的双圈图实验包含于两圈距离为1的双圈图实验.

分别用置信传播算法和纠正置信传播算法对各类带附加树的无公共边的二元双圈进行5 000次仿真实验,计算全局收敛率和正确率.结果见表4和表5.由表4和表5可知无论有没有附加树,无公共边的二元双圈均100%收敛,且纠正置信与正确边际的配置相同.

表4 两圈距离为1的二元双圈与附加树的收敛率和正确率

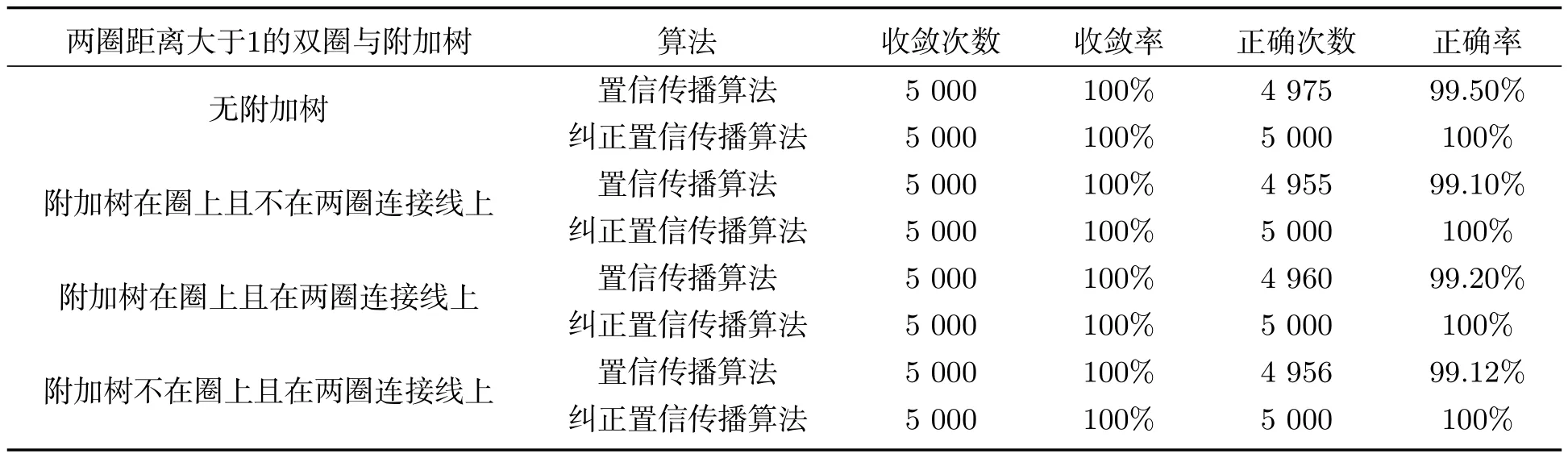
表5 两圈距离大于1的二元双圈与附加树的收敛率和正确率

6 结论

1）无公共边的双圈图全局收敛的条件: 无公共边的双圈图中任一消息有(n为迭代次数),则该图全局收敛.

2）置信传播算法在无公共边的双圈图(双圈和带有附加树的双圈)上均全局收敛,仿真实验得出两类图收敛率均为100%.

3）仿真实验得出:对于无公共边的双圈图(双圈和带附加树的双圈),稳态置信与正确边际分布不同,配置可能相同;二元稳态纠正置信与正确边际分布完全相同.