某型号汽车波纹管结构参数优化研究

2023-05-30黄晓雨王召宇薛克敏

合肥工业大学学报（自然科学版） 2023年5期

刘超, 黄晓雨, 王召宇, 刘蕾, 薛克敏, 李萍

(合肥工业大学材料科学与工程学院,安徽合肥 230009)

0 引言

金属波纹管是用多个横向波纹沿伸缩方向连接成的管状元件,是管道的连接和补偿装置,由于其所用材料具有耐高温、耐腐蚀、耐疲劳的特点[1],并且结构上具有很好的柔性,能在管道任意方向上进行位移补偿、吸收管道振动,从而起到减振、降噪的作用,因此被广泛应用在汽车、机械制造、化工、电力、仪表等工业领域。经过不断发展,金属波纹管现已应用于于航空、航天、船舶等尖端行业,具有广阔的应用前景[2-4]。

近年来,国内外学者对金属波纹管的振动特性、疲劳寿命、结构刚度、成形工艺等进行了研究[5-7]。波纹管在实际使用中,两端分别与发动机和排气管相连,当来自两端管路的激励力频率与波纹管本身固有频率相近时,会诱发结构间的共振,使波纹管结构产生振动损伤[8]。此外,波纹管在进行位移补偿时,会在波谷位置产生应力集中,较大的应力会降低波纹管的服役寿命[9]。而通过合理的结构参数优化能有效改善波纹管的振动特性和应力集中,延长波纹管的服役寿命。然而目前对于综合考虑波纹管振动损伤以及位移损伤的结构参数优化方面的研究还较少,结构优化设计方法也有待发展。因此,通过合理的优化设计方法对波纹管结构参数进行优化的研究十分必要。

本文以某型号汽车波纹管为研究对象,建立波纹管的模态分析及静力学分析有限元模型,基于单因素法研究不同结构参数对其固有频率以及伸长变形时最大应力值的影响规律,从而为正交试验设计提供依据;通过正交试验设计、极差分析、方差分析对结构参数进行优化,通过提高波纹管的固有频率以及降低位移补偿时的最大应力值来提高其抗振性能以及位移补偿能力;最终获得最优的结构参数组合并进行模拟验证,从而为同类型的波纹管结构参数优化设计提供一定的参考。

1 有限元建模过程

1.1 波纹管结构参数

某型号汽车波纹管及其主要结构参数如图1所示。该型号波纹管为单层波纹管,主要结构参数如下:波纹管内径d为107.8 mm;波高h为12.2 mm;波谷曲率半径r为1.3 mm;厚度t为0.2 mm。该波纹管所用材料为321不锈钢,其主要材料属性见表1所列。

表1 321不锈钢材料属性

图1 波纹管及其结构参数示意图

1.2 模型导入与网格划分

首先将在UG软件中建立的几何模型导入到Ansys Workbench软件中,采用Modal模块和Static Structural模块进行模态分析及静力学分析。采用软件的自划分功能进行网格划分,并对局部圆角区域进行网格细化,整体网格数量约为1 546 680个。

1.3 边界条件

在Ansys Workbench材料库中进行自定义材料并赋予完成材料属性定义,边界条件的定义参考波纹管的实际服役工况。在模态分析中,因为波纹管在实际使用中两端分别与管路相连,所以其边界条件设置为两端固定。在静力学分析过程中,波纹管在服役中会产生轴向伸长来进行位移补偿,因此其边界条件设置为一端固定,另一端施加沿轴向的10 mm位移。

模态分析及静力学分析的边界条件设置如图2所示。

图2 边界条件示意图

通过在后处理中添加变形、等效应力等来提取相应结果。模态分析中提取一阶固有频率,静力学分析中提取模型最大等效应力数值。

2 结构参数的影响

因为波纹管具有薄壁结构且波形较为复杂,所以其关键结构参数会对波纹管在复杂工况下的振动特性和应力分布有着显著影响。本文运用单因素法研究壁厚(0.10～0.40 mm)、波高(11.0～14.6 mm)、波谷曲率半径(1.10～1.40 mm)、内径(101.2～134.2 mm)4个主要结构参数对波纹管一阶固有频率及最大应力值的影响规律,结果如图3所示。

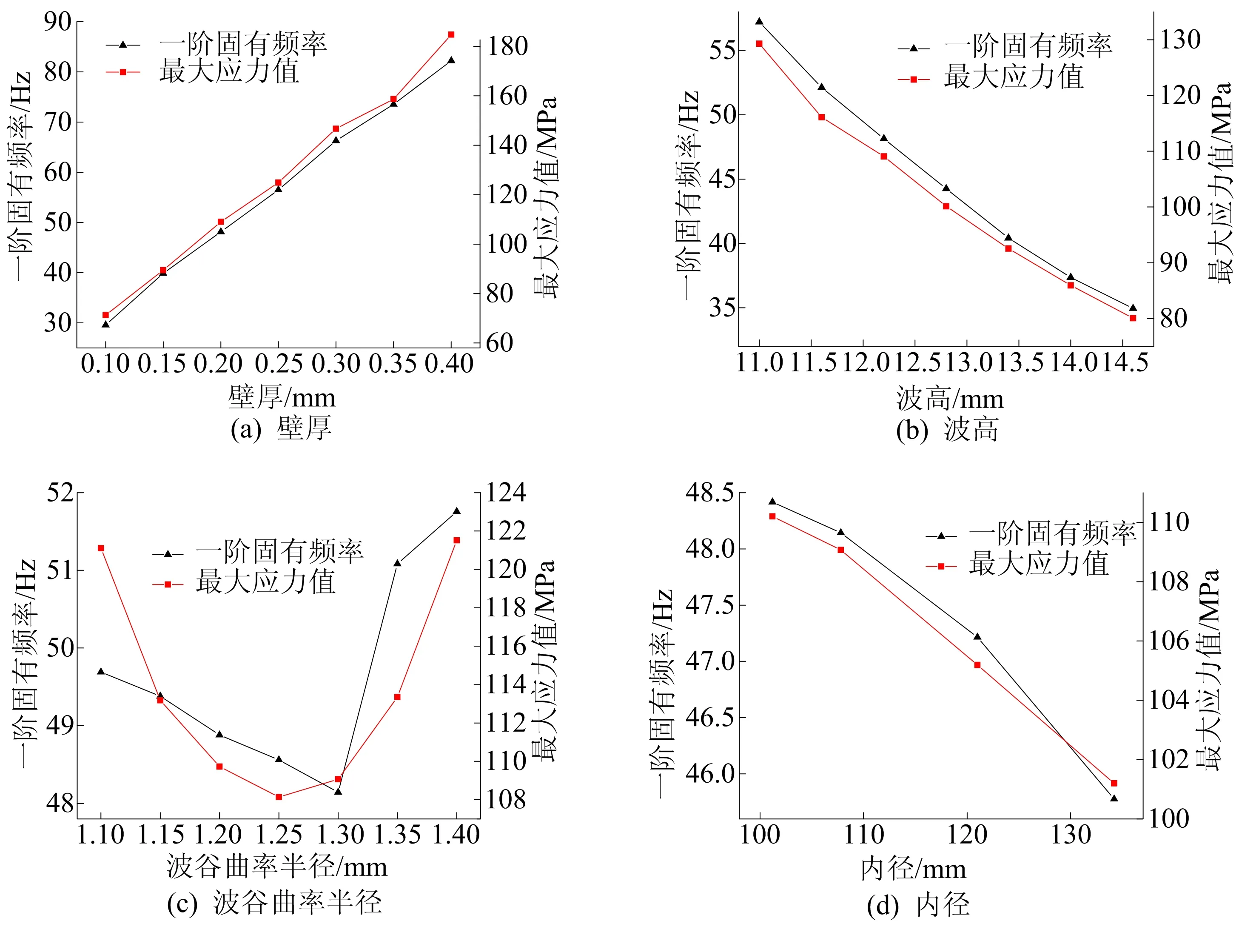
图3 不同结构参数对一阶固有频率及最大应力值的影响

2.1 壁厚的影响

壁厚是影响波纹管性能的重要结构参数。从图3a可以看出,随着壁厚不断增加,波纹管一阶固有频率及最大应力值均呈近似线性递增的趋势,一阶固有频率由29.90 Hz增加到82.23 Hz,最大应力值由71.33 MPa增加到184.00 MPa,因此2个指标的变化幅度较大,说明壁厚对2个指标的影响较为显著。

由于结构的固有频率只受刚度分布和质量分布影响,增加刚度和减小质量均会使结构固有频率增加[10]。而壁厚增加会增强波纹管的轴向、横向刚度[11],从而使结构的固有频率提高;但壁厚增加会增大最大应力值且降低波纹管的柔性,使波纹管的疲劳寿命下降[12]。

2.2 波高的影响

从图3b可以看出,与壁厚的影响相反,随着波高不断增加,波纹管一阶固有频率及最大应力值均呈近似线性递减的趋势,一阶固有频率由57.20 Hz减小到34.95 Hz,同时最大应力值由129.28 MPa减小到80.05 MPa,因此2个指标的变化幅度较大,说明波高会显著影响波纹管的服役性能。

波高的增加会使波纹管轴向刚度减小[13],因此当轴向产生相同的位移下,应力水平会更低,从而能延长波纹管的使用寿命。但结构刚度的减小会导致波纹管固有频率减小,较小的固有频率使波纹管易受低频激励的影响,使其在服役条件下的抗振性能下降[14]。

2.3 波谷曲率半径的影响

从图3c可以看出,随着波谷曲率半径的增加,波纹管一阶固有频率及最大应力值均先减小后增大。当波谷曲率半径为1.30 mm时,一阶固有频率取极小值48.14 Hz;当波谷曲率半径为1.25 mm时,最大应力值取极小值108.14 MPa。此外,随着波谷曲率半径的改变,2个指标的整体变化幅度较小,因此波谷曲率半径对2个指标的影响程度较小。

原因在于局部曲率半径的改变并不能显著改变整体结构的刚度特性和质量分布,因此结构的固有频率变化较小。因为刚度变化较小,所以在相同位移下应力水平变化也较小,从而对波纹管服役寿命影响较小。

2.4 内径的影响

从图3d可以看出,随着内径的增加,波纹管一阶固有频率及最大应力值均不断减小,但整体变化幅度较小。一阶固有频率仅从48.40 Hz下降到45.70 Hz,最大应力值从110.20 MPa下降到101.20 MPa,这表明内径对服役性能的影响程度较小。

这是由于改变内径不会影响到波形的结构,无法显著改变整体刚度特性,但会增加波纹管的整体质量,从而使固有频率下降。同时,该结果说明改变内径并不能显著降低波纹管的最大应力值。

3 波纹管结构参数优化

3.1 正交试验设计

结构参数对固有频率及最大应力值的影响是多因素综合作用的结果,仅通过单因素法无法获得最优的结构参数组合。而正交试验设计是利用数理统计学和正交性原理的一种高效试验设计方法,能有效地得出最优水平组合。因此,取壁厚、波高、波谷曲率半径和内径为试验因素,各取3个水平,取波纹管一阶固有频率和最大应力值作为试验指标,不考虑因素间的相互作用。在实际中,一般希望有较大的一阶固有频率以及较小的最大应力值。

利用L9(34),即4因素3水平标准正交表进行试验设计,因素水平表见表2所列。

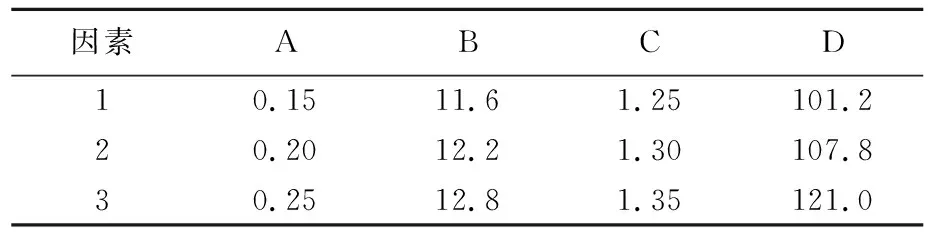
表2 因素水平表单位:mm

3.2 正交试验结果及分析

3.2.1 极差分析

对不同结构参数组合的波纹管进行三维建模,并进行模态分析及静力学分析,得到的各组试验方案及结果见表3所列。

表3 试验方案及结果

对2个试验指标进行极差分析,结果见表4所列。

表4 极差分析结果

由表3可知:一阶固有频率最大的为7号试验,其水平组合为A3B1C3D2;最大应力值最小的为3号试验,其水平组合为A1B3C3D3。

由表4可知,对于一阶固有频率,最优的因素组合为A3B1C1D2,根据极差R大小得出各因素影响的主次顺序为壁厚A、波高B、内径D、波谷曲率半径C;对于最大应力值,最优的因素组合为A1B3C2D3,各因素影响的主次顺序为壁厚A、波高B、内径D、波谷曲率半径C。

3.2.2 方差分析

方差分析的结果见表5所列。从表5可以看出:对于一阶固有频率,壁厚、波高、波谷曲率半径、内径的影响贡献值分别为81.697 6%、17.835 2%、0.017 6%、0.449 6%,即对一阶固有频率的影响显著程度依次为壁厚、波高、内径、波谷曲率半径,与极差分析结果相一致;对于最大应力值,壁厚、波高、波谷曲率半径、内径的影响贡献值分别为80.821 4%、9.612 0%、2.069 1%、7.497 5%,即对最大应力值的影响显著程度依次为壁厚、波高、内径、波谷曲率半径,也与极差分析结果相一致。

表5 正交试验方差分析结果

3.2.3 最优方案及试验验证

综上所述,因为对应2个指标各因素的优水平选择均相互矛盾,所以需通过综合平衡法来选出最优方案。

从试验结果可以看出,波纹管的最大应力值均远小于屈服强度,且波纹管在实际使用中主要受到来自振动的损伤,因此在进行优水平选择时应将一阶固有频率作为优先参考指标。从极差分析和方差分析可以看出,相对于最大应力值,因素A、因素B对一阶固有频率的影响显著程度更高,因此因素A、因素B的优水平组合应选择为A3B1。同时,相对于一阶固有频率,因素C、因素D对最大应力值的影响显著程度更高,因此因素C、因素D的优水平组合应选择为C2D3。综上,波纹管的最优结构参数组合应为A3B1C2D3,即壁厚为0.25 mm、波高为11.6 mm、波谷曲率半径为1.30 mm、内径为121.0 mm。

由于最优方案不在9组试验中,需要追加验证试验。验证试验的结果以及优化前、后的试验指标对比见表6所列。从表6可以看出:结构参数优化后的波纹管一阶固有频率由48.143 Hz增加到60.327 Hz,提升了25.3%;最大应力值由109.07 MPa增加到130.89 MPa,但其应力大小仍远小于屈服强度。因此,一阶固有频率的提高意味着波纹管低阶固有频率能避开低频激励的频率范围(0～50 Hz),从而避免共振的产生,提高波纹管在服役条件下的抗振性能。