2023年全国高考三角命题预测

2023-05-30梁业兴

广东教育·高中 2023年2期

梁业兴

纵观近年高考，三角内容的命题往往是“两小一大”，且“一大”常规会与解三角形、平面向量结合.试题难度中等及以下，对于考生来说是基础题、是普遍可以得分之题.因此，此类题很重要，它才是真正拉开距离的题，为了确保你不被对手“拉开”，你必须保证这些题“毫无悬念”的产生正确结论.它是你的“助力器”，它从命题的角度，结合试题类型进行全方位的剖析与预测，对你的复习与提升将会有帮助，请仔细往下看：

预测一：从基本技能入手，设计精巧的客观性试题

三角中的客观性试题并不一定都是基础题、简单题，有时它会与其它章节的知识结合在一起，从某一基本知识点或某一技能处进行设计，往往试题新颖、独特，求解艰苦有难度也有灵活性.

例1.（1）已知函数f（x）=3sin（2ωx+π3）（ω>0）的

图像与x轴相邻两个交点的距离为π2.若将f（x）的图像向

左平移m（m>0）个单位长度得到函数g（x）的图像恰好经过点（－π3，0），则当m取得最小值时，g（x）在［－π6，7π12］上的单调递增区间为______．

（2）已知α，β，γ是互不相同的锐角，则在sinαcosβ，sinβcosγ，sinγcosα三个值中，大于12的个数的最大值是（）

A. 0

B. 1

C. 2

D. 3

（3）如图，圆O的半径为1，A是圆上的定点，P是圆上的动点，角x的始边为射线OA，终边为射线OP，过点P作直线OA的垂线，垂足为M，将点M到直线OP的距离表示为x的函数f（x），则y=f（x）=＼[0，π＼]上的图像大致为（）

解析：（1）由函数f（x）的图像与x轴相邻两个交点的距离为π2，得函数f（x）的最小正周期为T=2π2ω=πω=1，函数f（x）的解析式为f（x）=3sin（2x+π3）.将f（x）的图像向左平移m（m>0）个单位长度得到函数g（x）=3sin［2（x+m）+π3］的图像，根据g（x）的图像恰好经过点（－π3，0），得sin2（－π3+m）+π3=0即m=kπ2+π6（k∈Z）.

因为m>0，所以m的最的小值为π6.此时，g（x）=3sin2x+2π3.

因为x∈－π6，7π12，所以2x+2π3∈π3，11π6.

当2x+2π3∈π3，π2，即x∈－π6，－π12时，g（x）单调递增.

当2x+2π3∈3π2，11π6，即x∈5π12，7π12时，g（x）单调递增．

综上，g（x）在区间－π6，7π12上的单调递增区间是－π6，－π12和5π12，7π12.

（2）由基本不等式有sinαcosβ≤sin2α+cos2β2，同理sinβcosγ≤sin2β+cos2γ2，sinγcosα≤sin2γ+cos2α2，

故sinαcosβ+sinβcosγ+sinγcosα≤32，故sinαcosβ，sinβcosγ，sinγcosα不可能均大于12.取α=π6，β=π3，γ=π4，则sinαcosβ=14<12，sinβcosγ=64>12，sinγcosα=64>12，

故三式中大于12的个数的最大值为2．故选C.

（3）如下图：过M作MD⊥OP于Ｄ，则 PM=｜sin x｜，

OM=cosx，在Rt△OMP中

，MD=OM·PMOP=cosx·sinx1=cosxsinx=12sin2x，

∴f（x）=12sin2x（0≤x≤π），选B.

点评：（1）本题包含了函数图像的多种基本性质，稍有不慎或有一处不过关，想产生结论都非常困难.（2）本题基本不等式与同角三角函数关系的巧妙结合，再加上一定的分析判断，恰到好处地产生了结论.（3）本题隐含了函数的解析式，如果你能顺利地产生函数解析式，最后产生結论就易如反掌.

预测二：设计多选题，从多角度、多层次考查基础知识与基本技能

多选题对于数学（Ⅰ）卷来说是后起之秀，虽然才进入试卷两年，但已引起了全体数学教师及高考命题人员的广泛关注.它可以横向考查多个知识点与技能点，有一个未掌握或未理解，本题你可能就只得两分.也可以纵向考查对某一知识与技能掌握的深度，尚若深度未达标，得分也很少.三角是设计各种类型多选题的“良田”，一定要引起我们重视.

例2.（1）使sinαcosβ=－13，使cosαsinβ成立的一个必要不充分条件是（）

A.－23，43______

B.－34，34

C.－43，43

D.－23，23

（2）已知定义域为R的函数f（x）满足f（1+x）+f（1－x）=0，函数g（x）=f（x）sinωx（ω>0），若函数y=g（x+1）为奇函数，则ω的值可以为（）

A.π4

B. π2

C.π

D. 3π2

（3）对于函数f（x）=sinπx，0≤x≤212f（x－2），x>2下列结论中正确的是（）

A.任取x1，x2∈［1，+），都有|f（x1）－f（x2）|≤32

B. f（12）+f（52）+…+f（12+2k）=2－12k+1，其中k∈N

C.f（x）=2kf（x+2k）（k∈N*）对一切x∈［0，+）恒成立

D. 函数y=f（x）－ln（x－1）有3个零点

解析：（1）ABC.设t=cosαsinβ，由sinαcosβ+t=sin（α+β），

sinαcosβ－t=sin（α－β）t+13≤1，

13－t≤1－23≤t≤23，选项D是充要条件.

（2）BD.由于定义域为R的函数f（x）满足f（1+x）+f（1－x）=0，所以f（x）的图像关于（1，0）成中心对称，所以f（x+1）的图像关于原点对称，所以f（x+1）奇函数，又因为函数y=g（x+1）为奇函数，因为g（x+1）=f（x+1）sinωx（ω>0）为奇函数，所以g（x+1）=f（x+1）sinω（x+1）（ω>0）为奇函数，∴hx+1=sinωx+ω为偶函数，∴ω=kπ+π2，k∈Z，ω的值可以为π2或3π2，故选BD．

（3）ACD.函数f（x）=sinπx，0≤x≤2

12f（x－2），x>2

的图像如图所示，得fmax（x）=1，fmin（x）=－1．

对于A：任取x1，x2∈［1，+），都有|f（x1）－f（x2）|≤|fmax（x）－fmin（x）|=12－（－1）=32.故A正确.

对于B：因为f12=1，f52=12，…，f12+2k=12k，f12+f52+…+f12+2k=2－12k.故B错误.

对于C：由f（x）=12f（x－2），得到f（x+2k）=12kf（x）f（x）=2kf（x+2k）.故C正确.

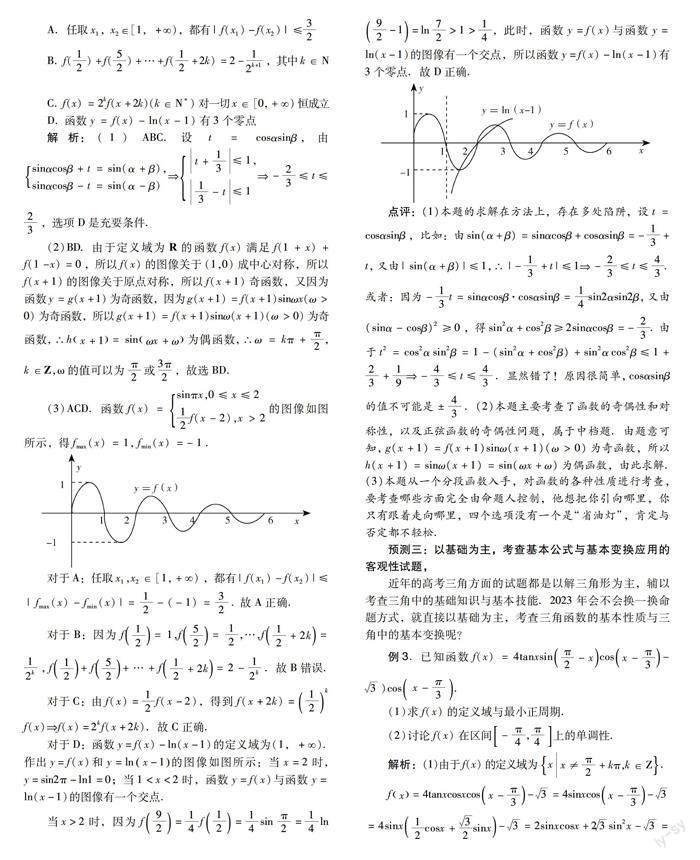
对于D：函数y=f（x）－ln（x－1）的定义域为（1，+）.作出y=f（x）和y=lnx－1的图像如图所示：当x=2时，y=sin2π－ln1=0;当1

当x>2时，因为f92=14f12=14sinπ2=14ln92－1=ln72>1>14，此时，函数y=f（x）与函数y=ln（x－1）的图像有一个交点，所以函数y=f（x）－ln（x－1）有3个零点.故D正确．

點评：（1）本题的求解在方法上，存在多处陷阱，设t=cosαsinβ，比如：由sin（α+β）=sinαcosβ+cosαsinβ=－13+t，又由|sin（α+β）|≤1， ∴|－13+t|≤1 －23≤t≤43.或者：因为－13t=sinαcosβ·cosαsinβ=14sin2αsin2β，又由（sinα－cosβ）2≥0，得sin2α+cos2β≥2sinαcosβ=－23.由于t2=cos2αsin2β=1－（sin2α+cos2β）+sin2αcos2β≤1+23+19－43≤t≤43 .显然错了！原因很简单，cosαsinβ的值不可能是±43.（2）本题主要考查了函数的奇偶性和对称性，以及正弦函数的奇偶性问题，属于中档题．由题意可知，g（x+1）=f（x+1）sinω（x+1）（ω>0）为奇函数，所以h（x+1）=sinω（x+1）=sin（ωx+ω）为偶函数，由此求解．（3）本题从一个分段函数入手，对函数的各种性质进行考查，要考查哪些方面完全由命题人控制，他想把你引向哪里，你只有跟着走向哪里，四个选项没有一个是“省油灯”，肯定与否定都不轻松.

预测三：以基础为主，考查基本公式与基本变换应用的客观性试题，

近年的高考三角方面的试题都是以解三角形为主，辅以考查三角中的基础知识与基本技能.2023年会不会换一换命题方式，就直接以基础为主，考查三角函数的基本性质与三角中的基本变换呢？

例3.已知函数f（x）=4tanxsinπ2－xcosx－π3－3）cosx－π3.

（1）求f（x）的定义域与最小正周期.

（2）讨论f（x）在区间－π4，π4上的单调性.

解析：（1）由于f（x）的定义域为xx≠π2+kπ，k∈Z.

fx=4tanxcosxcosx－π3－3=4sinxcosx－π3－3

=4sinx12cosx+32sinx－3=2sinxcosx+23sin2x－3

=sin2x+31-cos2x－3=sin2x－3cos2x=2sin2x－π3.

所以，fx的最小正周期T=2π2=π.

（2）令z=2x－π3，函数y=2sinz的单调递增区间是－π2+2kπ，π2+2kπ，k∈Z.

由－π2+2kπ≤2x－π3≤π2+2kπ，得－π12+kπ≤x≤5π12+kπ，k∈Z.

设A=－π4，π4，B=x－π12+kπ≤x≤5π12+kπ，k∈Z，易知A∩B=－π12，π4.

所以，当x∈－π4，π4时，f（x）在区间－π12，π4上单调递增，在区间－π4，－π12上单调递减.

点评：此题很基础、很简单，把它设计为解答题的第一题，也就是第17题完全可以.三角函数是以角为自变量的函数，因此解三角函数题，首先从角进行分析，善于用已知角表示所求角，即注重角的变换.角的变换涉及基本公式，选用恰当的公式，是解决三角问题的关键. 对于三角函数来说，常常是先化为y=Asin（ωx+φ）+h的形式，再利用三角函数的性质求解．三角恒等变换要坚持结构同化原则，即尽可能地化为同角函数、同名函数、同次函数等，其中切化弦也是同化思想的体现.降次是一种三角变换的常用技巧，要灵活运用降次公式．

预测四：以分析探索为主，设计探索性客观性试题

探索性试题，一直倍受各级各类考试命题人的青睐，以分析探索为主，设计三角函数的探索性试题也可能是命题方向之一.

例4.已知函数f（x）=sinωx（sinωx+cosωx）－12（ω>0）图像的相邻两条对称轴之间

的距离为2π．

（1）求f（x）的单调递增区间以及f（x）图像的对称中心坐标.

（2）是否存在锐角α，β，使α+2β=2π3，fα+π2·f2β+3π2=38同时成立？若

存在，求出角α，β的值.若不存在，请说明理由．

解析：（1）由f（x）=sinωx（sinωx+cosωx）－12=22sin2ωx－π4.

因为f（x）图像的相邻两条对称轴之间的距离为2π，得T=4π=2π2ωω=14.

于是f（x）=22sin12x－π4.

由－π2+2kπ≤12x－π4≤π2+2kπ－π2+4kπ≤x≤3π2+4kπ（k∈Z）.

所以f（x）的单调递增区间为－π2+4kπ，3π2+4kπ（k∈Z）.

由12x－π4=kπx=2kπ+π2（k∈Z）.

所以f（x）图像的对称中心坐标为2kπ+π2，0（k∈Z）.

（2）存在，理由如下：

因为fα+π2=22sinα2，f2β+3π2=22sinβ+π2=22cosβ，

那么fα+π2·f2β+3π2=22sinα2·22cosβ=12sinα2cosβ.

由α+2β=2π3α=2π3－2β，

得sinα2cosβ=sin（π3－β）cosβ=

32cosβ－12sinβcosβ

=32·1+cos2β2－14sin2β=34+34cos2β－14sin2β.

即fα+π2·f2β+3π2=38+38cos2β－18sin2β.

若fα+π2·f2β+3π2=38，则38cos2β－18sin2β=0tan2β=3.

又β为锐角，得β=π6，由α+2β=2π3α=2π3－2β=π3.

点评：本题主要考查了三角函數恒等变换的应用，正弦函数的周期公式，正弦函数的图像和性质的综合应用，考查了转化思想和运算求解能力，属于较难题．（1）由已知利用三角函数恒等变换的应用可得函数解析式f（x）=22sin2ωx－π4，利用正弦函数的周期公式可求ω的值．进一步得到增区间以及对称中心．（2）由已知利用三角函数恒等变换的应用可求tan2β=3，结合范围β为锐角产生结论．

预测五：注重选择性，设计条件或结论不完备的客观性试题

条件或结论不完备试题是近年才出现的，由于它具有选择性，而试题的难易与运算的

繁简又不可能绝对一致，因此，恰当的选择（或运气的选择）也许会使求解简单一些，因此，它很受考生喜欢，当然，也受到命题专家的关注.

例5.在①f（x）的图像关于直线x=5π6ω对称，②f（x）=cosωx－3sinωx，③

f（x）≤f（0）恒成立这三个条件中任选一个，补充在下面问题中．若问题中的ω存在，求出ω的值，若ω不存在，请说明理由．

设函数f（x）=2cos（ωx+φ）（ω>0，0≤φ≤π2），______，是否存在正整数ω，使

得函数f（x）在0，π2上是单调的？（注：选择多个条件分别解答，按第一个解答计分）

解析：若选①，令ωx+φ=kπ，k∈Z代入x=5π6ωφ=kπ－5π6，因为0≤φ≤π2，

所以φ=π6，f（x）=2cosωx+π6，当x∈0，π2时，ωx+π6∈π6，πω2+π6.

若函数f（x）在0，π2上单调，则有ωx2+π6≤π0<ω≤53，

所以存在正整数ω=1时，使得函数f（x）在0，π2上单调的;

若选②，f（x）=cosωx－3sinωx=2cosωx+π3φ=π3，

当x∈0，π2时，ωx+π3∈π3，πω2+π3，

若函数f（x）在0，π2上单调，则有πω2+π3≤π0<ω≤43，

所以存在正整数ω=1时，使得函数f（x）在0，π2上是单调的.

若选③，因为f（x）≤f（0）恒成立，即f（x）max=f（0）=2cosφ=2cosφ=1.

因为0≤φ≤π2，所以φ=0此时f（x）=2cosωx，当x∈0，π2时，ωx∈0，πω2，

若函数f（x）在0，π2上单调，则有πω2≤π0<ω≤2，

所以存在正整数ω=1或2时，使得函数f（x）在0，π2上是单调的．

点评：本题考查三角函数的图像与性质，属于开放性的中档题．若选①，要注重在对称轴处取得最大值或最小值.若选②，要注重“化一公式”的应用.若选③，要注重函数最值的特点．无论选哪一个都需要抓住0，π2是函数的一个单调区间的子区间即可.

预测六：从实际应用入手，设计与生活实际联系密切的客观性试题

数学建模是数学的六大核心素养之一，是高考重点考查的内容.用所学知识处理实际应用问题的能力又是数学的重要能力，从实际应用入手设计与生活实际联系密切的客观性试题完全在情理之中，当然，要注意试题的难度.

例6.如图，我市某污水处理厂要在一个矩形污水处理池ABCD

的池底水平铺设污水净化管道（Rt△FHE三条边，H是直角顶点）来处理污水，管道越长，污水净化效果越好.要求管道的接口H是AB的中点，点E，F分别落在线段BC，AD上，已知AB=20m，AD=103m，记∠BHE=θ．

（1）试将污水净化管道的总长度L（即Rt△FHE的周长）表示为θ的函数，并求出定义域;

（2）问θ取何值时，污水净化效果最好·并求出此时管道的总长度．

解析：（1）由题意可得EH=10cosθ，FH=10sinθ，EF=10sinθcosθ，

由于BE=10tanθ≤103，AF=10tanθ≤10333≤tanθ≤3π6≤θ≤π3.

所以L=10cosθ+10sinθ+10sinθcosθ，θ∈π6，π3.

即L=10×sinθ+cosθ+1sinθcosθ，θ∈［π6，π3］.

（2）设sinθ+cosθ=t，则sinθcosθ=t2－12，

由于θ∈π6，π3，t=sinθ+cosθ=2sinθ+π4∈3+12，2，

由于L=10（t+1）t2－12=20t－1在3+12，2上是单调减函数，

所以，当t=3+12时，即θ=π6或θ=π3时，L取得最大值为203+1m.

点评：本题考查三角函数在实际问题中的应用、两角和与差的三角函数，考查转化思想以及计算能力，是中档题，也是完全可能作为考题的题，值得我们关注．

预测七：从新定义入手，设计与基本技能相关的客观性试题

新定义问题一直是高考命题的热点，在三角函数中设计一道中档题，用以考查三角函数的基础知识与基本技能是一个很好的创意，值得我们关注.

例7.设函数f（x）=cos2x+asinx+a．

（1）当a=1时，求函数f（x）在区间0，π3上的值域;

（2）设函数φ（x）的定义域为I，若x0∈I，且φ（x0）=1，则称x0为函数y=φ（x）的

“壹点”，已知f（x）在区间［0，2π］上有4个不同的“壹点”，求实数a的取值范围．

解析：由于f（x）=cos2x+asinx+a=－2sin2x+asinx+a+1，

（1）当a=1时，f（x）=－2sin2x+sinx+2，x∈［0，π3］，易得值域为3+12，178．

（2）由题意可知，－2sin2x+asinx+a+1=1在区间［0，2π］上有4个不同的零点，

令g（x）=－2sin2x+asinx+a，则g（x）在区间［0，2π］上有4个零点，令t=sinx∈［－1，1］，则h（t）=－2t2+at+a，

①若h（t）在（－1，1）上有2个非零零点，则

h（－1）<0，

ha4>0，

h（1）<0，

－1

h（0）≠00

②若h（t）的2个零点为0和1，则

a=0，

a2=1，无解，舍去.

③若h（t）的2个零点为0和－1，则

a=0，

a2=－1，无解，舍去．

综上所述，0

点评：本题考查了二倍角公式的应用，换元法求三角函数值域，二次函数根的分布，属于难题．（1）先利用余弦的二倍角公式，将原函数变形，然后换元法，变成关于t的二次函数，再求函数的值域，需要注意新元的取值范围.（2）将题干描述的“壹点”可以转化为函数的零点问题来处理，再结合二次函数根的分布，分类讨论每种情况．

预测八：从与其他知识点交汇点入手，设计新颖的客观性试题

试题的交汇性也是高考试题的一大亮点，曾经的概率统计与数列交汇、立几与导数交汇等都让人们记忆犹新，其实数学中的所有内容几乎都是可可交汇的，只是看命题人如何进行设计.

例8.设函数f（x）=2acos2x+（a－1）cosx－1，其中a>0，记|f（x）|的最大值为A．

（1）若a≥1，求A.

（2）证明：|f′（x）|≤2A

解析：（1）当a≥1时，|f（x）|=|2acos2x+（a－1）cosx－1|=|acos2x

因此，A=3a－2.

（2）当0

则A是|g（t）|在［-1，1］上的最大值.g（-1）=a，g（1）=3a-2，

且当t=1-a4a时，g（t）取得极小值，极小值为g1-a4a=-a2+6a+18a．

令-1<1-a4a<1，得a<-13（舍去），或a>15．

（i）当0