关注几何图形的确定性 提高试题命制的科学性

孔原平

[摘  要] 科学性是试题命制最基本的准则. 本文提出在命制初中几何试题时，要理清图形结构特征，关注几何图形的确定性;合理呈现表达形式，提高试题命制的科学性;加强一题多解研究，破除惯性思维的局限性.

[关键词] 几何图形;确定性;科学性;命题思考

试题命制是教师专业化道路上不可或缺的一项重要的基本技能，它是日常教学工作的延伸. 一套高质量的试题既能体现立德树人的根本任务，又能发挥教育教学作用，对教育教学效果做出客观、科学的评价. 然而，在初中数学试题命制的实践过程中，题目设置不科学的现象时有发生，尤其是初中几何中的计算题，在命题中稍有疏忽，就会出现问题. 文章中的例题是笔者在中考复习课堂上收集到的试题，试图通过本文与初中数学教师进行沟通交流关于试题命制时应注意的问题.

真题再现

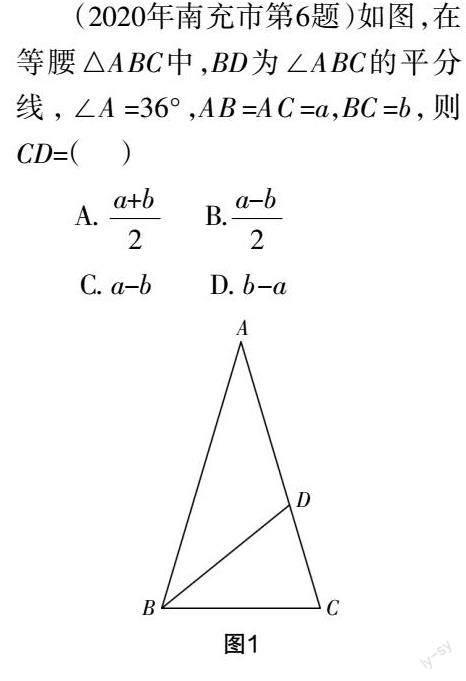
（2020年南充市第6题）如图，在等腰△ABC中，BD为∠ABC的平分线，∠A=36°，AB=AC=a，BC=b，则CD=（     ）

A.   B.

C. a-b      D. b-a

试题分析

本题图形简洁，条件清晰，问题明确，是中考中一道非常普通和简单的几何题. 命题人把这道题放到选择题的第6题，显然是把它看作是一道容易题，学生得分率也应该较高.

试题是通过黄金三角形为背景，立足对三角形内角和，角平分线的定义，等腰三角形的性质与判定，以及线段的和差等知识点的考查. 虽然涉及的知识点较多，但都是较为容易掌握的基础知识. 学生只需通过观察、猜想、演绎推理，将等腰三角形的底边转化到腰上，再通过线段的加减即可解决问题. 本题考查了学生的识图能力、分析问题、解决问题的能力，简单中蕴含了丰富的几何知识以及对基本技能的考查.

解法探究

解法一  因為∠A=36°，AB=AC，所以∠ABC=∠C=72°.

因为BD平分∠ABC，所以∠ABD=∠DBC=36°，∠A=∠ABD=36°，∠BDC=∠C=72°.

所以AD=BD，BC=BD，AD=BC=b.

又因为AC=a，所以CD=a-b. 故选C.

解法一无懈可击，命题人也应该是这样设想的，肯定大多数学生也能得到正确选项C. 可是，一个城市的中考考场上少则几万，多则十多万学生在考试，难道他们的想法都会按照命题人的设想去思考吗？我们不能排除学生可能会有以下解法.

解法二  由解法一可得∠DBC=∠A=36°.

又因为∠C=∠C，所以△BDC∽△ABC.

所以=，即=，所以CD=.

解法三  利用角平分线和平行线组合，巧妙构建新的等腰三角形，再利用相似三角形的性质解答本题.

如图2，过点D作DE∥/AB交BC于点E，所以△DEC∽△ABC，=.

由法一得∠ABC=∠C=72°，所以∠DEC=∠C=72°，所以DE=DC.

又因为∠ABD=∠DBC=36°，所以∠ABD=∠BDE=36°，∠DBC=∠BDE，所以BE=DE，BE=DC，所以EC=b-CD ，即=.

所以CD=.

解法四  如图3，过点D作DE∥CB交AB于点E，

所以∠DBC=∠EDB，=.

因为∠A=36°，AB=AC，所以∠ABC=∠C=72°，AE=AD，所以BE=DC.

又因为BD平分∠ABC，所以∠DBE=∠DBC，所以∠DBE=∠EDB，△EDB∽△DBA.

所以BE=ED，DC=ED，=，所以CD=.

解法二、解法三和解法四主要都是利用相似三角形的判定与性质求CD的长. 这种解法在几何学习中，对图形的相似变换掌握较好的学生，往往能够根据题目条件自然联想到的方法.

解法五  如图4，作AE⊥BC于点E，BF⊥DC于点F.

因为AB=AC，所以CE=BC.

由法一得BD=BC，所以CF=DC.

在Rt△BFC中， cosC=;在Rt△AEC中，cosC=.

所以=，即=，所以CF=;

所以CD=2CF=.

解法五利用同一个角的三角函数值是定值建立等量关系，巧妙的求出CD的值. 虽然该方法也需要证明△ABD与△BDC是等腰三角形，与解法一比较明显复杂得多，但解法一与解法五是从两种不同的角度思考解决问题的策略.

寻根解惑

五种解法得出三个不同的答案，笔者也感觉困惑，它们之间是否存在一定的内在联系，是否可以统一为一个相同的结果？带着这个疑问，笔者继续探究发现将a-b，，这三个式子中任意两个相等，化简后均可得a2-ab-b2=0，解得a=b或b=a，将a=b或b=a分别代入三个不同的答案，最终都得到CD=b或CD=a这两个相同的结果.

用正弦定理和倍角公式，也能说明a与b之间的确存在内在的关联. 因为在△BDC中，=，即=，化简得DC=①;在△ABC中，=，化简得a=2bcos36°②.①÷②得DC=.

通过以上探究，说明该三角形中a与b之间的确存在内在的关系. 也正是这个原因，使我们在解答这个题时，由于解题路径不同导致呈现的结果不相同. 这种题目设置不科学的现象，导致试题对教育教学效果不能给出客观、科学的评价.

命题思考

1. 理清图形结构特征，关注几何图形的确定性

为什么会有上述情况发生？这就不得不说到图形的确定性——只要图形的形状确定了，那么该图形的内角度数，各边长度之间的比例关系就是确定的，由此得到的该几何图形的各种性质也是确定的. 该例题图形中由∠A=36°，AB=AC，就说明△ABC的形状已经确定，只是大小不确定，但其腰长与底边的比==2cos36°是确定的值. 同样根据题目条件可知△DBC与△ABD都是等腰三角形，他们的底角分别是72° 和36° ，它们的形状也是确定的，那么它们腰长与底边的比也应该是一个确定的值. 也正是这个原因，导致三种不同的计算结果，但经验证它们都是正确的.

所以，编制一道几何试题时，教师必须对问题本质、图形结构、相互之间数量关系与位置关系有充分的认识，在给出数据时，要认真思考图形中是否存在“量”之间的制约关系，充分考虑各个条件是否具有相容性，以免出现试题不科学的现象.

2. 合理呈现表达形式，提高试题命制的科学性

《教育部关于加强初中学业水平考试命题工作的意见》要求依据课程标准科学命题，提高命题质量，明确指出客观性试题要有确定的答案. 科学性、正确性、逻辑性、规范性、层次性、创新性等是试题命制中必须遵守的原则. 从专业化的眼光来看，命题必须首要注重科学性[1]. 科学性是任何考试都必须遵循的基础性原则[2]. 命制试题的过程中命题人必须用心思考，规避因题目的叙述或呈现形式的不科学所带来的偏差或风险，更不能因为题目设置不科学给考生带来心理恐慌. 如果将题目中的“CD=（     ）”改为“CD的长可以表示为（   ）” 这样的叙述就比较科学. 因为这样的描述表示下面有一个代数式是正确的，但并不排除还有别的表达形式. 試题中“D选项”是一个无效选项，因为“b-a”明显是一个负数，就相当于自然去掉一个选项. 如果改为设置更科学，更能体现题目的思维含量和知识的覆盖面.

3. 加强一题多解研究，破除惯性思维的局限性

作为一名数学教师，尤其是教学经验教为丰富的教师，往往会凭经验和直觉去思考问题，导致教学行为和解决问题方法单一化，模式化. 笔者在没有任何暗示的情况下，让八位数学教师各自做这道题，结果七位教师不到1分钟都给出了答案C. 一位教师开始得出了CD=，但一看选项中没有这个答案，略加思考，改成了选C. 可惜！他没有对本题提出质疑. 8位教师给出了同一个答案，究其原因就是教师们有了固化的几何模型或几何自觉所导致. 所以，教师在日常教研中，要有意识地从多角度思考问题，透过现象看本质，通过一题多解探寻直达思维本质的自然解法[3]. 因此，破除惯性思维的局限性，加强一题多解研究，对试题命制的科学性和合理性有十分重要的作用.

中考是每个初中生学习生涯中重要的一次人生大考. 考场上任何情绪上的波动都可能给考生造成一定的心理压力. 试卷中的考题设置不科学，会给考生带来较大的心理压力，甚至会造成较大的负面影响[4]. 再者，中考题对教师的教学也具有很强的导向作用. 所以中考命题，肩负着巨大的社会责任，容不得半点纰漏. 它既要关注知识、能力、素养的考查，又要注重适当难度、有效信度和恰当区分度的设置，还要关注试题的科学性、合理性和严谨性[5].

总之，中考试题的命制工作是一项复杂的系统工程，每一道中考试题都必须经命题专家组反复论证、精雕细琢，才算交付了一份满意的答卷. 一线教师在平常的试题命制中，同样应该加强研究，提升试题命制能力，在命题中提升自己的专业素养.

参考文献：

[1]庞灵锋. 从一道试题的改编谈试题命制的科学性[J].  数学教学通讯，2014（18）：53-55.

[2]张会杰. 试题命制的科学性：结构要素及其技术规范[J]. 考试研究，2019（01）：59-64.

[3]沈丹. 一道中考几何题的解答探究与拓展思考[J]. 中学数学教学参考，2021（05）：25-27.

[4]张宁. 中考命题中存在的问题及建议——以2014年全国各地中考试题为例[J]. 中学数学杂志，2015（02）：60-63.

[5]刘成龙. 中考数学命题错误分析[J]. 中学数学，2020（14）：70-72.