培养学生能力 提高学生意识

陈结洪

一、课标要求分析

用待定系数法求二次函数解析式是函数知识考查中最基本的要求，纵观每年的全国中考题都离不开二次函数的考查与运用。解析式也就是函数的表达式或者关系式，它是基础题最基本的表达形式，也是压轴题的基础，在哲学角度理解为“经济基础”，是综合其他知识的纽带，促使学生用数学的眼光观察世界，用数学的思维思考现实世界，用数学的语言表达世界。

二、学情分析

授课学生为分层教学的实验生，知识水平相对平稳，但也有部分学生在理解和运算能力上比较偏弱一点。用待定系数法求二次函数解析式涉及三种表达形式，同时考查应用的背景灵活多变，所以学生在学习运用三个坐标点代表一般式的知识基础下深入探究顶点式和交点式，有很好的衔接作用，更能加深对综合题的应用，体会解析式在函数应用中的地位与作用。

三、教学目标

1. 由已知抛物线的顶点式到设置顶点坐标为参数，通过对用待定系数法求参数的过程探究，掌握求解析式的基本方法；一题多解，提高审题和解题能力，从而选取合适的解析式模式解题。

2. 数与形相结合，提升用待定系数法求抛物线的解析式的速度。

3. 培养学生分析问题、解决问题的能力，提高学生用数学的意识，渗透几何直观、运算能力等核心素养。

四、教学重难点

教学重点：会用待定系数法求抛物线的解析式。

教学难点：能选择最优的方法求得抛物线的解析式并初步运用相应的解析式解决数学问题。

五、教学方法

基于问题创设导向教学、“四整合”兵教兵分层布局、鸿合电子白板交互融合教学等方法。

六、教学过程

（一）复习引入

1．（1）抛物线y＝3（x＋4）2＋5的顶点坐标是（， ）；（2）抛物线y＝a（x－h）2＋k的顶点坐标是（， ）。

2．已知抛物线y＝a（x－1）2＋k过点（0，7）和（-1，13），求抛物线的解析式和顶点坐标。

【设计意图】

（1）熟悉顶点式，能从顶点式中提炼出顶点坐标，为设顶点式求解析式做铺垫。

（2）第2题是对待定系数法解参数和还原解析式进行巩固训练。

（3）归纳总结：①设：表达式；②代：坐标代入；③解：方程（组）；④还原：写表达式。

（4）让学生理解求解析式的原因。

（二）核心主题，主动交流

经典例题：

1. 已知抛物线的顶点为（-2，1），且图象过点（-4，-3），求抛物线的解析式。

解：∵抛物线顶点为（-2，1）

∴设二次函数解析式为y＝a（x＋2）2＋1

再把点（-4，-3）代入，得：

4a＋1＝-3，解得：a＝-1，

∴所求的二次函数的解析式为y＝－（x＋2）2＋1，即：y＝－x2－4x－3。

2. 探究：可以设一般式解这道题吗？（联想已学知识思考）

3. 归纳：解题步骤，解题格式，精准解题。

4. 小结：

（1）设置脚手架模式引入，侧重于格式的培养，调动学生学习积极性。

（2）总结二次函数图象上一点和顶点坐标，求二次函数解析式，一般将二次函数的解析式直接设为顶点式y＝a（x－h）2＋k（a≠0），再将另外一点坐标代入求出a值，最后写回解析式。

（三）探索比较，一题多解

1. 变式训练

（1）已知二次函数的图象过点（0，-3），并且当x＝-2时，y有最大值1。

①求这个二次函数的解析式；

②把二次函数的图象沿坐标轴方向如何平移可使该图象的顶点在原点？

追问：求函数解析的目的是什么？达到什么效果？

③用草图画出二次函数图象，并求二次函数图象与x轴的交点坐标；

追问：讨论，能否从本小题中归纳出一种简便的求解析式的方法？需要已知什么条件？形式是什么？注意关注什么？

（2）总结归纳：中考题，变式迁移。

（3）抛物线上部分点的横坐标、纵坐标的对应值如下表所列：

請选择合适的方法，求此抛物线的函数解析式。

【设计意图】

目的：利用问题串形式，启发学生思考。这样每一个问题都成为学生思维的阶梯，使学生在明确知识内在联系的基础上获得知识、提高思维能力。

重视审题分析，让学生通过审题过程，调用顶点式进行求解析式。把例题变换背景，培养学生总结能选择什么类型的解析式求解。

2. 深度研题

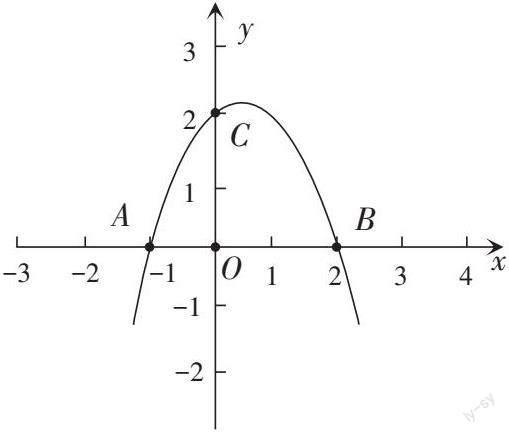
（1）已知某二次函数的图象如图所示交x轴于A、B点，交y轴于C点，顶点为D。

①求此二次函数的解析式；

②求点D的坐标及△ABD的面积。

（玩转数学变式题）

（2）①动点P（x，3）能否在抛物线上？请说明理由；

②若点A（a，y1），B（b，y2）都在抛物线上，且a＜b＜0，比较y1，y2的大小，并说明理由；

③保持抛物线的顶点坐标不变，且抛物线与x轴两交点间的距离为4，求此抛物线的函数关系式；

④已知二次函数的图象如图所示，求此抛物线的解析式。

（你能有几种方法求解？）

【设计意图】

（1）设计目的：学生通过观察比较，总结由一个题而引申的多个问题，在活动中，让学生自己去观察、发现、总结，实现学生主动参与、探究新知的目的。

（2）数形结合，体会提炼几何背景下求解析式的应用能力。通过归纳，培养学生抽象概括能力。同时培养了学生与他人合作的能力，增强了学生的团队合作意识。

（3）通过数形结合，求到解析式，能化简成顶点式。求得顶点坐标进而为求三角形的面积做铺垫。利用几何画板演示动点的变化，体会面积的变化，为续学习沿垂法做铺垫。

（四）课堂小结

1. 求二次函数解析式的方法选择。

2. 理清题意，找出已知条件。

3. 题中知顶点或对称轴，优设顶点式，最后考虑一般式。

4. 一设，二代，三解，四还原。

5. 格式严谨，稳步得分，立足中考。

【设计意图】

（1）通过创设问题形式为主线，用问题串方式把需要学习和探究的内容设置到每个小问中，让学生体会对知识的总结归纳，了解为什么要用这个知识去解题，解题的目的是什么，怎样才能做到最优化、高效。

（2）总结各种方法的特点，把握各种方法的应用背景。

七、教學反思

1. 整合大单元教学模式，通过已知二次函数的顶点式去寻找顶点坐标，再到参数下的顶点式，使学生体会到由数到代数的变化过程。

2. 教学例题设置脚手架模式引入，侧重于格式的培养，调动学生学习积极性。每个问题都成为学生思维的阶梯，使学生在明确知识内在联系的基础上获得知识、提高思维能力。

3. 通过几何画板进行教学与技术赋能相结合，动态演示二次函数图象的生成过程和位置以及特别交点式的规律。

4. 通过玩转数学变式题，巩固求解析式，强化二次函数解析式的性质应用。数形结合，求到解析式，能化简成顶点式，求得顶点坐标进而为求三角形的面积做铺垫。利用几何画板演示动点的变化，体会面积的变化，为继续学习沿垂法做铺垫。

5. 探究“融·乐”课堂教学模式。

（1）理论层面：本课例创新点是可操作性，不再是理论上的“纸上谈兵”，而是实践性的，我们这个课例正是解决了广大教师最头疼的问题，大家都了解理论，就是不知道如何操作，我们就是着力于问题创设的具体做法和有效的提问设计。

（2）实践层面：本课例的特色是从学生的实际需求出发，体现“生本”思想，让学生之间、师生之间通过自主研究、民主探索、平等合作、发现问题、解决问题，相互启发、共同提高实践创新能力、增加学习质量和个体素质，形成一种生动活泼、潜力无穷、人人参与、主动积极学习的活动形式。本校“四整合”教学模式与“研学案”教学相结合，有利于实现“双减”目标。