两版高中数学教材中“问题提出”的比较研究

胡典顺 朱展霖

摘要：在编码统计的基础上，从分册分布、板块分布、类型分布、情境分布、主题分布、素养分布等六个维度进行分析，对新旧人教A版高中数学教材必修分册中的“问题提出”内容（引导学生提出问题的任务——主要包括问题情境和引导语）进行比较研究。由此，对教材编写提出一些建议：豐富“问题提出”内容设计的角度，激发学生思维动力；优化“问题提出”内容设计的梯度，提升课堂互动质量；挖掘“问题提出”内容设计的深度，鼓励批判创新精神。

关键词：高中数学；问题提出；教材比较

一、 研究缘起

爱因斯坦认为，提出一个问题往往比解决一个问题更重要，因为解决问题也许只需要数学上或实验上的技能，而提出新的问题却需要创造性的想象力，并且标志着科学的真正进步。［1］在数学学习、研究过程中，学生提出问题，不仅有助于深入理解所学知识并挖掘知识背后蕴含的本质，从而提高核心素养，还能从中捕捉到并创造出新知识产生的源泉。［2］

“问题提出”是指基于一定的问题情境，通过某种意义上的重构来提出问题的过程，这一过程贯穿于“问题解决”中。［3］近年来，“问题提出”受到各国数学教育研究者的重视。在国内，除了义务教育数学课程标准和普通高中数学课程标准不断强调包括发现问题和提出问题在内的“四能”目标之外，不少研究者从情境视角、现状调查、能力评价、教材比较、培养策略等方面对“问题提出”进行了研究［4］。其中，教材比较为“问题提出”提供了静态的研究视角，有利于深入挖掘各个版本教材中“问题提出”内容（引导学生提出问题的任务——主要包括问题情境和引导语）蕴含的价值，以及为教材的编写提供改进建议。在国内教材的比较研究方面，宋运明等对四版小学数学教材中的“问题提出”提示语进行了统计分析［5］；胡典顺等对两版小学数学教材中的“问题提出”内容进行了比较［6］。在与国外教材有关的比较研究方面，胡典顺等对中美三版小学数学教材中的“问题提出”内容进行了对比［7］；严卿等对中日两版初中数学教材中“问题提出”内容进行了比较［8］。但总体而言，国内关于“问题提出”尤其是数学教材方面的研究并不多，且没有对高中数学教材的研究。

本文对依据《普通高中数学课程标准（实验）》编写的和依据《普通高中数学课程标准（2017年版）》（以下简称“新课标”）编写的人教A版高中数学教材（分别出版于2007年和2019年，以下分别简称“旧教材”和“新教材”）必修分册中的“问题提出”内容进行比较研究，以期为教材编写（乃至课程改革）提供一些建议。

二、 研究过程与结果

在研究的过程中，我们阅读教材并记录有关“问题提出”的内容，进行编码统计，进而从分册分布、板块分布、类型分布、情境分布、主题分布、素养分布等六个维度进行分析。

由于两版教材在编排结构、板块（栏目）设计上存在一些差别，因此，我们在研读时，基于两版教材的共同特点，分板块（栏目）对教材中的“问题提出”内容进行编码统计。（1） 对于例题、练习等板块中的“问题提出”，若没有小题设置，则按照题号编码统计；若有小题设置，则按照小题号编码统计。（2） 对于思考类栏目（包括穿插于正文中的“思考”“观察”“探究”等栏目）中的“问题提出”，若设置了题号，则按照题号编码统计；若没有设置题号，则按照整个栏目编码统计。（3） 对于章前语、正文、标注、小结、复习巩固等板块和拓展类栏目中的“问题提出”，若设置了明显的题号，则按照题号编码统计；若没有设置题号，则根据语句或段落，综合实际语境编码统计。

（一） “问题提出”的分册分布

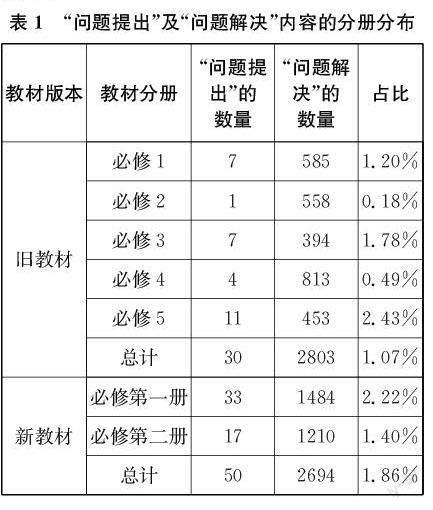
旧教材包括5个必修分册，新教材包括2个必修分册。两版教材各必修分册中“问题提出”内容及“问题解决”内容的数量如表1所示。

从两版教材中“问题提出”内容的分册分布情况来看，新教材中“问题提出”内容的总数比旧教材有显著增加（z=2.43，p<0.05）；“问题提出”内容在“问题解决”内容中的占比也有所增加，但仍然处于较低水平（均低于1.9%）。

（二） “问题提出”的板块分布

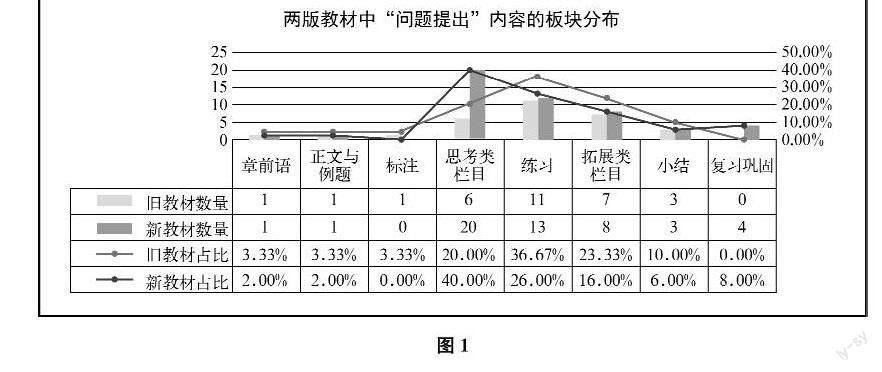
教材中不同板块（栏目）的内容，对学生学习有着不一样的作用（价值），并且能从多个角度帮助学生深入理解和挖掘知识间的联系。结合两版教材的编排结构，将两版教材中的板块（栏目）分为课程引入、课程设计和课后巩固三大类。其中，课程引入对应章前语；课程设计包括正文与例题、标注、思考类栏目；课后巩固包括练习、拓展类栏目、小结、复习巩固。两版教材中“问题提出”内容的板块分布如图1所示。

两版教材中“问题提出”内容的板块分布整体上没有显著差异（Fisher检验，p=0.23>0.05），均集中在思考类栏目、练习、拓展类栏目中，而较少在章前语、正文与例题、标注等中。在思考类栏目、练习、拓展类栏目中，新教材中“问题提出”内容的数量比旧教材中有所增加，但比例上没有显著变化（z=1.85，p>0.05；z=1.01，p>0.05；z=0.81，p>0.05）。在章前语、正文与例题、小结中，两版教材中“问题提出”内容的数量相同，比例也没有显著变化（z=0.37，p>0.05；z=0.37，p>0.05；z=0.66，p>0.05）。此外，新教材在复习巩固中增设了4个“问题提出”内容，而删除了标注中的1个“问题提出”内容，但比例上没有显著变化（z=1.31，p>0.05；z=1.59，p>0.05）。

（三） “问题提出”的类型分布

“问题提出”内容（引导学生提出问题的任务）可以分为以下五类。一是数学猜想型：通过设置情境，启发学生提出数学猜想或发现数学规律。例如，新教材必修第一册第230页的“观察分析等式sin2 30°+cos2 60°+sin 30°cos 60°=34，sin 220°+cos2 50°+sin 20°cos 50°=34，sin2 15°+cos2 45°+sin 15°cos 45°=34的共同特点，写出能反映一般规律的等式，并对等式的正确性作出证明”。

二是运算给定型：通过设置数学式子、函数或变量关系等，要求学生设计相应的问题情境。例如，新教材必修第一册第63页的“试构建一个问题情境，使其中的变量关系可以用解析式y=x（10－x）来描述”。

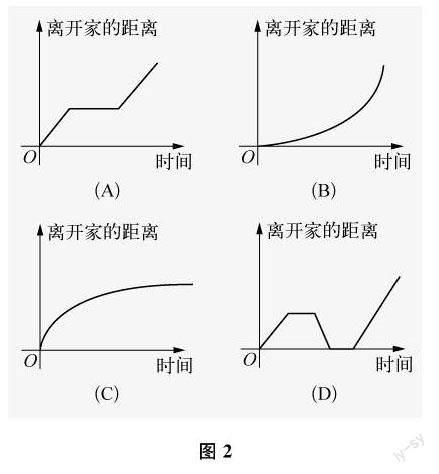
三是补充型：通过设置没有完整条件或问题的情境背景，要求学生将条件或问题补充完整。例如，旧教材必修1第23页的“下页图2中哪几个图像与下述三件事分别吻合得最好？请你为剩下的那个图像写出一件事。（1） 我离开家不久，发现自己把作业本忘在家里了，于是返回家里找到了作业本再上学；（2） 我骑着车一路匀速行驶，只是在途中遇到一次交通堵塞，耽搁了一些时间；（3） 我出发后，心情轻松，缓缓行进，后来为了赶时间开始加速”。

四是追问型：介绍相关知识背景或解决相关问题之后，要求学生构建新的情境，提出新的问题并解决。例如，旧教材必修3第93页的“你能试着对自己身边的某个问题，确定两个变量，通过收集数据，计算相关系数，然后分析一下能否用线性回归模型来拟合它们之间的关系吗”。

五是数学活动型：让学生通过搜集资料、与同学交流等活动进行探究学习，从而将所学知识与自己的想法联系起来并提出问题。例如，新教材必修第二册第189页的“你可能想了解全校同学生活、学习中的一些情况，例

如，全校同学比较喜欢哪门课程，每月的零花钱平均是多少，喜欢看《新闻联播》的同学的比例是多少，每天大约什么时间起床，每天睡眠的平均时间是多少，等等。选一些自己关心的问题，设计一份调查问卷，利用简单随机抽样方法调查你们学校同学的情况，并解释你所得到的结论”。

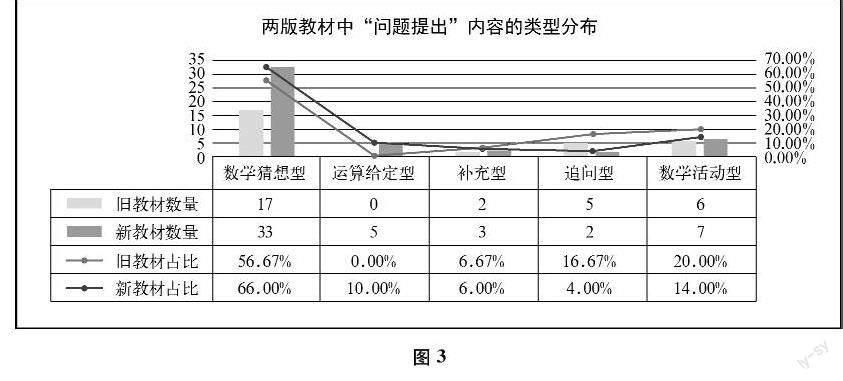
两版教材中“问题提出”内容的类型分布情况如图3所示。

两版教材中“问题提出”内容的类型分布整体上没有显著差异（Fisher检验，p=0.124>0.05），都主要是数学猜想型，其次是数学活动型，较少是运算给定型、补充型和追问型。新教材中数学猜想型、补充型、数学活动型“问题提出”内容的数量比旧教材均有所增加，但比例上没有显著变化（z=0.83，p>0.05；z=0.12，p>0.05；z=0.7，p>0.05）；追问型“问题提出”内容的数量有所减少，但比例上没有显著变化（z=1.94，p>0.05）。此外，新教材增设了运算给定型的“问题提出”内容。

（四） “问题提出”的情境分布

新课标将教学与评价的情境划分为现实情境、数学情境、科学情境等三类。两版教材中“问题提出”内容的情境分布如下页表2所示。

两版教材中“问题提出”内容的情境分布趋势上没有显著差异［χ2（1，80）=3.484，p=0.062>0.05］，均主要基于数学情境，其次基于现实情境，而没有基于科學情境的。新教材中基于数学情境的“问题提出”内容的数量比旧教材增加了几乎两倍，且比例上有极其显著的变化（z=9.87，p<0.01）；基于现实情境的“问题提出”内容的数量减少了2个，但比例上没有显著变化（z=0.8，p>005）。

（五） “问题提出”的主题分布

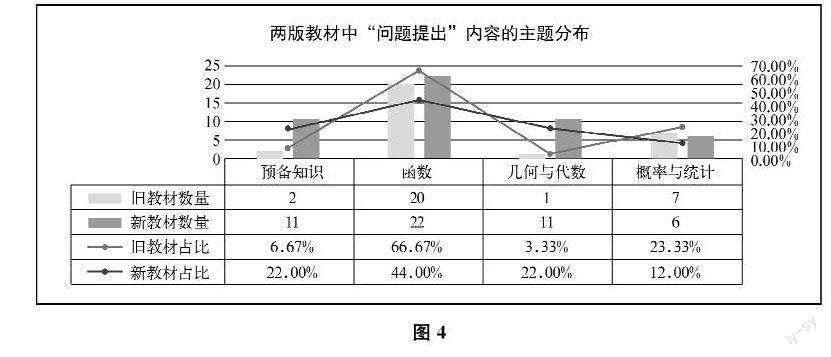
新课标将课程划分为预备知识、函数、几何与代数、概率与统计、数学建模活动与数学探究活动等五个主题。其中，数学建模活动与数学探究活动贯穿于其他四个主题中。两版教材中“问题提出”内容的主题分布如图4所示。

两版教材中的“问题提出”内容均集中分布在函数主题中，相对较少地分布在其他主题中，但整体上有显著变化（Fisher检验，p=0.015<0.05）。新教材中预备知识主题下“问题提出”内容的数量比旧教材有所增加，

但比例上没有显著变化（z=1.80，p>0.05）；函数主题下“问题提出”内容的数量有显著增加，但比例上有显著下降（z=1.97，p<005）；几何与代数主题下“问题提出”内容的数量与比例都有非常显著的增加（z=2.26，p<0.01）；概率与统计主题下“问题提出”内容的数量与比例均有所下降，但没有显著变化（z=1.33，p>0.05）。

（六） “问题提出”的素养分布

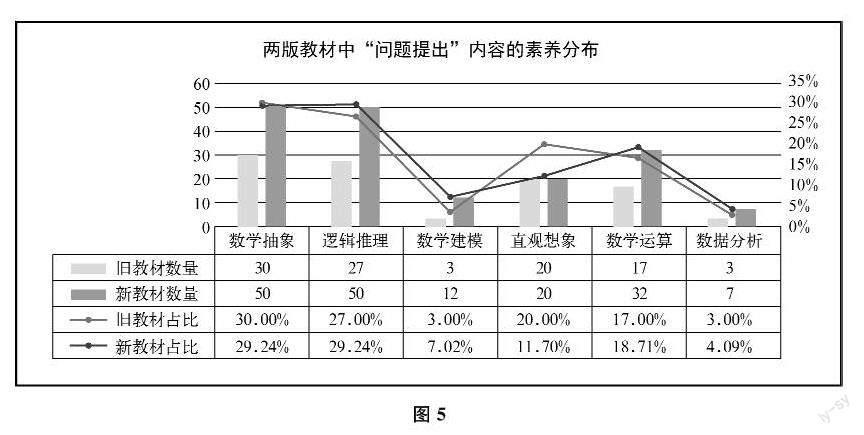
新课标将数学核心素养分为数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析等六个维度。不同的“问题提出”内容重点融入（主要培养或考查）的数学核心素养不同。两版教材中“问题提出”内容的素养分布如下页图5所示。

两版教材中“问题提出”内容的素养分布整体上没有显著差异（Fisher检验，p=0.416>0.05），均与数学抽象素养、逻辑推理素养高度相关，与数学建模素养、数据分析素养的相关程度较低。这在一定程度上体现出数学抽象能力与逻辑推理能力在数学学习中重要的奠基作用。具体而言，新教材中与数学抽象素养、逻辑推理素养有关的“问题提出”内容的数量比旧教材有显著增加（z=2.263，p＜0.05；z=2.2792，p<0.05）；与数学建模素养、数据分析素养相关的“问题提出”内容的数量有所增加，但比例上没有显著变化（z=1.55，p>0.05；z=0.52，p>0.05）；与直观想象素养有关的“问题提出”内容的数量没有变化（z=2.31，p<0.05）；与数学运算素养有关的“问题提出”内容的比例没有显著变化（z=0.65，p>0.05）。

三、 研究启示：对教材编写的几点建议

（一） 丰富“问题提出”内容设计的角度，激发学生思维动力

教材中“问题提出”内容设计的丰富，对学生思维的发展有重要的引导和启发作用。第一，要丰富设计的类型。不同类型的“问题提出”内容对学生提出问题的角度和思考的方式有着不一样的引导作用。例如，运算给定型“问题提出”内容能引导学生赋予自身熟悉的意义，从而丰富对数学式子的理解；补充型和追问型“问题提出”内容能引导学生通过提问，对某一个具体的知识点进行深入的加工和思考。第二，要丰富设置的板块。将“问题提出”内容设置于不同板块，对教学过程中教师的预设和学生的生成有着重要的导向作用。例如，在章节末尾设置构建思维导图梳理知识从而提出问题的任务，有利于学生对知识的充分反思和深入总结。第三，要丰富设置的情境。情境对“问题提出”有着重要的启发意义。教材中基于科学情境的“问题提出”内容较少。数学是科学发展的基础，科学的进步与国家的兴盛紧密相连。从科学情境出发，有利于调动学生数学学习的积极性，帮助他们在科学情境的探究中树立爱国情怀和远大理想。此外，两版教材中几何领域的“问题提出”内容都较少，而几何是中学阶段培养直观想象、数学抽象、逻辑推理等思维能力的重要内容，因此教材可考虑在几何方面加强设计。只有从多元化的角度去设计“问题提出”内容，才能充分激发学生的思维动力。

（二） 优化“问题提出”内容设计的梯度，提升课堂互动质量

教材中“问题提出”内容的设计还需要“脚手架”：适当的梯度设计能够帮助学生有效梳理知识并建构思维框架，降低学生提出优质问题的难度，从而引导学生体会思考和提出问题的过程和方法。一方面，要优化语言设计的精确性。教材中的语言对学生思维和课堂教学的开展有着重要的指导作用，而准确的语言设计也是教学目标和课堂价值得以实现的重要保证，不同的提问方式对学生思考的积极性和思考的方向、深度的影响有着显著的差异。因此，“问题提出”内容的语言设计要尽可能精简、准确、连贯、自然、生动，保证能有效引导学生提出符合教学目标且有价值的问题。另一方面，还要注重培养学生举一反三，多角度把握数学本质的能力。因此，“问题提出”内容可以增加一些引导学生改变题目中的已有条件，对比改变前后的解题方法、结论等，从而在对比中把握本质的类型。例如，对上文所举的运算给定型“問题提出”例子，可以引导学生改变函数解析式中的常数或者运算符号，通过对比改变前后的结果和解答过程，深入感受这类解析式的本质特点和在实际情境中的意义。

（三） 挖掘“问题提出”内容设计的深度，鼓励批判创新精神

培养学生提出问题的能力是数学教学的重要目标之一，而更长远的意义在于引导学生学会将该能力迁移到其他学科以及社会生活的独立思考和批判性思维中。因此，数学教材中“问题提出”内容的设计应该有更高的立足点，在凸显数学教学目标的同时，深刻体现育人价值。一方面，要注重数学思想方法的挖掘。如果把数学知识比作建筑的砖瓦和基石，那么数学思想方法则是建筑设计的灵魂体现。在数学教学中，要注重数学思想方法对学生思维发展深度的深远影响。不少学生在未来的学习甚至工作中用不到太多和数学相关的知识，但是，解决数学问题的思考方式和具体方法能够在学习及生活中迁移和转化。例如，可以设计专题探究环节，引导学生对涉及同一种重要数学思想方法的题型进行总结归纳，并自己设计和提出问题。另一方面，应注重文化融合的多样性。不同领域的

文化是相互联系、相辅相成的。而只有将社会、科学、医学、艺术等不同领域的文化与数学相融合，才能很好地提升学生的思考深度，从而培养他们用数学的眼光看待世界的能力。

参考文献：

［1］ 张玲，宋乃庆，蔡金法.问题提出：基本蕴涵与教育价值［J］.中国电化教育，2019（12）：3139.

［2］ S.L.Shukkwan.On the role of creative thinking in problem posing［J］.ZDM，1997（3）：8185.

［3］ E.Silver， J.Cai.Assessing Students Mathematical Problem Posing［J］.Teaching Children Mathematics，2005（3）：129135.

［4］ 尚亚明，何忆捷，熊斌.中国数学问题提出研究的回顾与展望［J］.数学教育学报，2019（6）：8186.

［5］ 宋运明，夏小刚，张学杰.对小学数学教科书中“提出问题”提示语编写的思考和建议——基于四种版本教科书的统计与分析［J］.课程·教材·教法，2011（4）：5257.

［6］ 胡典顺，蔡金法，聂必凯.数学问题提出与课程演变：两个版本小学数学教材的比较［J］.课程·教材·教法，2015（7）：7579.

［7］ 胡典顺，薛亚乔，王明巧.中国和美国小学数学教材中问题提出的比较研究［J］.数学教育学报，2016（4）：3741.

［8］ 严卿，胡典顺.中国和日本初中数学教材中问题提出的比较研究［J］.数学教育学报，2016（2）：2025.