“拓展创新学程”函数主题编写特色及教学建议
2023-05-30丁菁葛军
丁菁 葛军




摘要:《普通高中拓展创新学程·数学》中的函数主题共设计了19个专题。其编写主要是对苏教版高中数学教材中有关函数的“活性”知识进行延伸、综合、覆盖、解构,从而引导学生适度拓展函数知识,深刻领悟函数思想,促进思维发展。对此,提出三点教学建议:合理选取内容,采用适合的学习形式;从简单问题出发,引导学生深度思考;落实“一题多解、一解多题、一题多题”。
关键词:高中数学;拓展创新学程;函数
函数是高中数学必修、选择性必修课程除了预备知识、数学建模活动与数学探究活动之外的三大主题(学习领域)之一。函数贯穿高中数学课程,将初等数学与高等数学连接起来。函数思想是数学思想的重要组成部分,也是中学数学的基本思想之一。
本文简单介绍《普通高中拓展创新学程·数学》(以下简称《拓展创新学程》)中函数主题的基本内容,重点阐述其编写特点和教学建议。
一、 基本内容
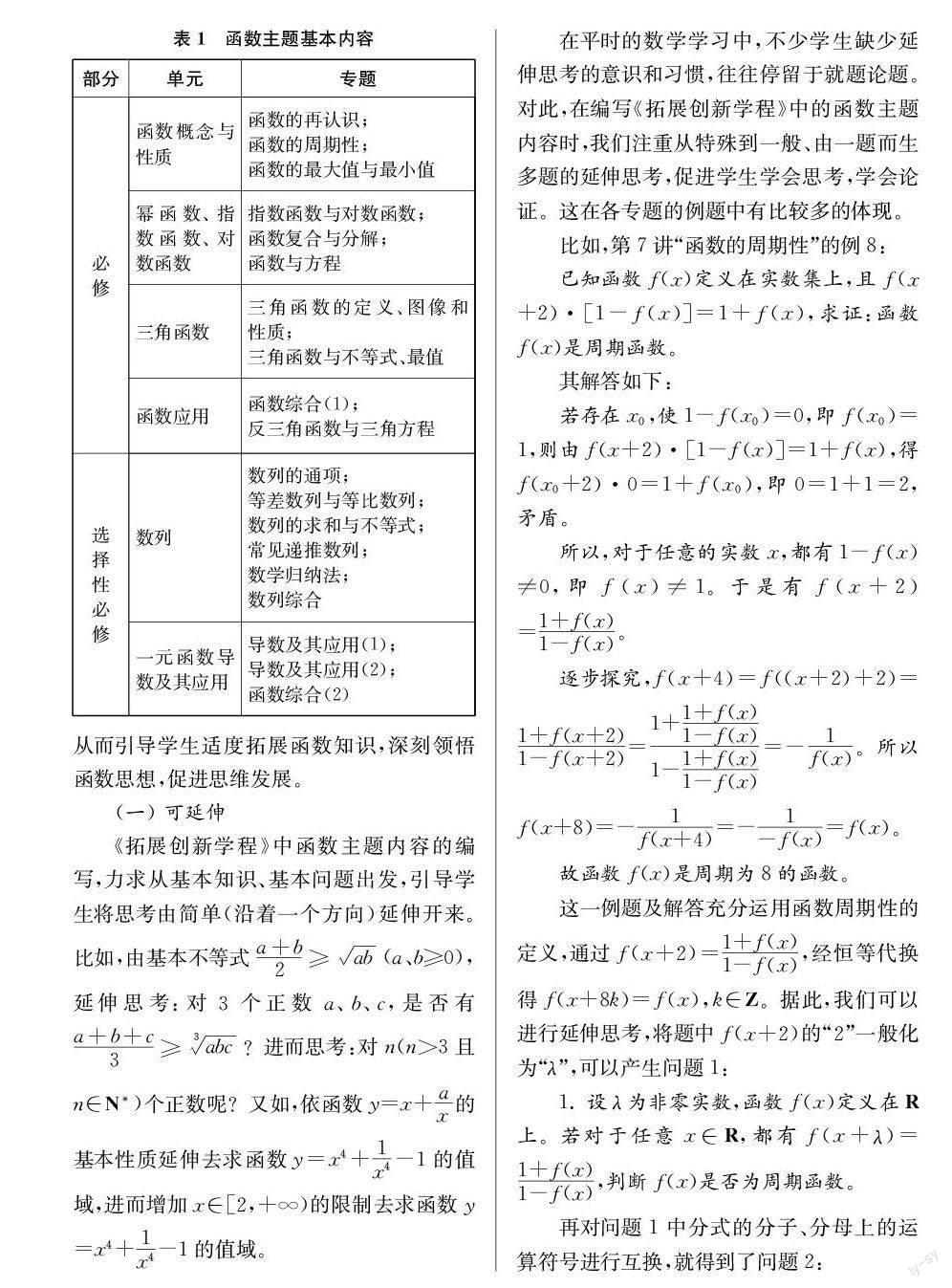
《拓展创新学程》中的函数主题以高中数学必修、选择性必修课程的函数内容为基础,共设计了19个专题(见下页表1)。
各个专题围绕函数的核心内容,对苏教版高中数学教材的相关内容做了延伸、补充和提高。比如,“函数的再认识”专题就延伸了对反函数的认识和对复合函数、函数迭代的认识,“反三角函数与三角方程”专题则补充了反三角函数的有关内容,等等。
二、 编写特色
《拓展创新学程》中函数主题内容的编写,主要是对苏教版高中数学教材中有关函数的“活性”知识进行延伸、覆盖、综合、解构,
三、 教学建议
《拓展创新学程》与苏教版高中数学教材同步配套,提供的是在教材学习的基础上开阔视野、培养解题能力、提升数学思维的专题学习。下面,对函数主题内容的教学提出三点建议,供广大一线教师参考。
(一) 合理选取内容,采用适合的学习形式
作为拓展创新内容,函数主题所选内容有一定的难度,因此,在教学中,应根据学生的学习情况、个性特征,合理选取内容,采用灵活多样的学习形式,尽可能地促进学生的发展。
比如,在高一阶段学习了“函数的基本性质”后,可以就“函数的再认识”“函数的周期性”“函数的最大值与最小值”等专题开设讲座;学习了幂函数、指数函数和对数函数的有关内容后,可开设“指数函数与对数函数”的专题讲座;学习了三角函数的有关内容后,可开设“三角函数的定义、图像和性质”的专题讲座。
又如,在高二阶段学习了“导数及其应用”后,可精选“导数及其应用(1)(2)”中的典型例题开展课堂教学,幫助学生认识和总结处理函数与导数问题的一般策略。此外,还可在高三阶段函数与导数部分的复习中,将这部分内容作为复习资料开展教学。这些综合问题的求解,不仅有助于加深学生对知识、方法的理解,更重要的是能帮助学生形成方法策略,达成能力提升。
除了上述学习形式外,在保证学生日常学习有余力的情况下,还可指导学生对“反三角函数与三角方程”等专题开展研究性学习,提交研究报告。
(二) 从简单问题出发,引导学生深度思考
对《拓展创新学程》中函数主题内容的教学,我们主张从简单问题出发,引导学生深度思考。“简单问题,深度思考”是指从基本问题出发,依据对象、元素、运算、图形等不同因子生长问题,在求解的过程中从解题方法上升到数学方法、数学思想。[1]
比如,对上述第7讲“函数的周期性”的例8,通过“对象”变化,可以生成相应的问题1和问题3;进而通过“运算”变化,可以生成相应的问题2和问题4。
这样做的意义在于,引导学生学会学习和思考,从学习解题方法走向体悟数学思想和方法,对问题所反映的事物性质、规律以及该事物与其他事物的内在联系形成深刻理解。
(三) 落实“一题多解、一解多题、一题多题”
对《拓展创新学程》中函数主题内容的教学,我们还主张“三一”法,即一题多解、一解多题、一题多题。
一题多解是指从不同的角度思考和解答一个数学问题,它有利于培养学生思维的灵活性,达到对知识和方法的融会贯通。但是,仅仅停留在一题多解的层面是不够的,许多不同数学问题的解决都运用了同一种数学思想方法,需要在解题中要加以提炼,形成一解多题,达成举一反三、触类旁通。而一题多题则是指通过一般化因子、运算因子、命题因子、图形因子等,将问题进行生长,以激发学习数学的兴趣,促进思维能力的提升和创新意识的发展,发展数学核心素养。
参考文献:
[1] 葛军,鲍玉曦.数学问题产生之“四字诀”——数学思维研究之一[J].教育研究与评论(中学教育教学),2015(11):3336.
