在“变”与“不变”中感悟本质

陶芳

摘要：为了让学生学会从变量的角度认识两种量之间的关系，初步感受函数的思想方法，《正比例的意义》一课教学，引导学生“变中识不变，变中思不变，变中知不变”。重要的节点包括：比较对照，感悟正比例的意义；多元表征，建构正比例的模型；操作体验，体会正比例的图像。

关键词：小学数学；变与不变；《正比例的意义》；函数思想

正比例关系是从对应的角度认识和研究两种相关联的量之间“变”与“不变”的规律。“对应”两个数量之间的“比值不变”是正比例关系的本质属性。从研究单个量走向多个量，从研究固定（具体）的量走向变化的量，从研究单个数据的静态情况走向多个数据的动态关系，是学生认识过程中的一次重大飞跃。同时，正比例的知识在日常生活中有着广泛的应用，学好这部分内容，既可以锻炼学生用数学的眼光观察现实生活的意识，提高思考现实问题的能力，又可以为学生初中进一步学习函数知识奠定扎实的基础。為了让学生学会从变量的角度认识两种量之间的关系，初步感受函数的思想方法，《正比例的意义》一课教学，引导学生“变中识不变，变中思不变，变中知不变”。

一、教学过程

（一）理解正比例意义中的“变”

1.通过猜拳游戏，理解“相关联”

（课始，教师让学生同桌玩“石头剪刀布”的游戏，赢一次得5分，共玩9次。游戏结束后，全班汇报得分。）

师 得分的多少和获胜的次数是有联系的。获胜的次数多，得分也多；获胜的次数少，得分也少。像这样“一种量变化，另一种量也随着变化”，我们称这两种量为“相关联的量”。

2.举例与辨析

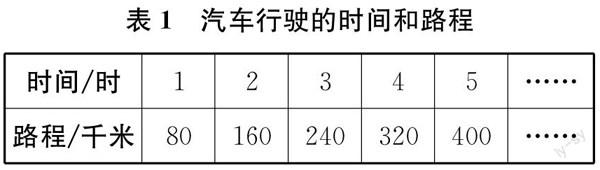
师 生活中相关联的量很多。（出示一辆汽车匀速行驶的时间和路程对照表，见表1）请大家认真研究：表格中有哪两种量？

生 行驶的时间和路程。

师 它们是相关联的量吗？为什么？

生 汽车行驶的时间长，行驶的路程也长，行驶的时间和路程同时增加；时间短，路程也短，时间和路程同时减少。所以，时间和路程是相关联的量。

师 行驶的时间和路程的变化是——

生 一致的。

师 请带着这样的思路继续研究这几张表中的数据。

（依次出示购买一种铅笔的数量和总价、读一本书时的已读页数和剩下页数、用同样多的钱购买不同的笔记本的单价和数量、正方形的边长和面积、小明的年龄和身高等对照表，见表2—表6。）

生 铅笔的数量和总价变化方向一致，二者是相关联的量。

生 已读页数和剩下页数变化方向不一致，但二者是相关联的量。

生 笔记本单价和数量变化方向不一致，但二者是相关联的量。

生 正方形的边长和面积变化方向一致，二者是相关联的量。

生 小明的年龄和身高不是相关联的量，因为年龄变化，身高不一定发生变化。

（二）理解正比例意义中的“不变”

1.独立探究，初步感知意义

师 根据刚才的分类，仔细观察表1、表2和表5这三张表，其中相关联的两种量变化方向都一致，那它们有没有什么变化规律呢？如果有，又是按什么规律变化的呢？（指表1）先来看表1，路程和时间在变化的过程中有什么规律呢？

（学生计算验证。）

生 路程和所对应的时间的比值都是80。

师 还真是这样的，那么，这个比值80就是汽车的——

生 速度。

师 所以，我们还可以用怎样的数量关系式来表示？

生 路程时间=速度（一定）。

师表2和表5中相关联的两种量又有怎样的变化规律呢？和你的同桌一起说一说，算一算，完成研究单。

（学生交流并完成研究单。）

生 （展示自己的研究单，如下页图1所示）表2中总价和数量是两种相关联的量，总价和数量的比值是不变的，也就是单价是一定的。数量关系为：总价/数量 =单价（一定）。

生 （展示自己的研究单，如图2所示）正方形的边长和面积是两种相关联的量，面积随着边长的变化而变化，但是面积和边长的比值是变化的，并不一定。

2.归纳总结，揭示正比例意义

师 同学们，刚才的三张表中，两种量的变化方向都是一致的，但是对应的两种量的比值有的一定，有的不一定。当比值一定时，我们就说两种相关联的量成正比例关系，这两种相关联的量是成正比例的量。比如，路程和时间是两种相关联的量，当路程和时间的比值一定，也就是速度一定时，我们就说路程和时间成正比例关系，路程和时间是成正比例的量。（板书：路程和时间成正比例关系）总价和数量成正比例关系吗？为什么？

生 总价和数量是两种相关联的量，总价和对应的数量的比值一定，也就是单价一定，所以总价和数量是成正比例的量。

师 这就是我们今天所要研究的正比例的意义。（板书课题：正比例的意义）比较一下，成正比例关系的两种相关联的量有什么特点？（板书：变化的量，不变的量）那正方形的边长和面积成正比例关系吗？为什么？

生 正方形的边长和面积的比值不一定，所以不成正比例关系。

师 看来，两种相关联的量，只有比值一定，才成正比例关系。那怎样来判断两种量是否成正比例关系呢？同桌互相说一说。

（学生讨论。）

师 看一看两种量是不是相关联的量，也就是“变”；算一算相关联的两种量的比值是不是一定，也就是“不变”。

3.抽象概括，建立模型

师 像这样比值一定的式子，写得完吗？

生 （齐）写不完。

师 如果用字母x和 y分别表示两种相关联的量，用k表示它们的比值，正比例关系可以用怎样的式子来表示？

［教师根据学生的回答板书：yx=k（一定）。］

（三）从正比例的意义到正比例的图像

师 判断正方形边长和周长是否成正比例。

（学生自主列出表7，并判断、说理。）

师 （出示下页图3）往同一个圆柱形杯子中倒水，水的体积和高度成正比例吗？为什么？

（学生回答。）

师 （出示下页图4）我们发现，当水的体积和高度成正比例关系时，把体积和高度的对应点连起来正好是一条直线。

二、教学思考

（一）“变”中识“不变”：比较对照，感悟正比例的意义

判断两个变量是否成正比例，首先要看这两个量是否相关联，而判断的核心是看这两个变量在变化过程中，比值是否一定。所以，让学生明确研究的方向是两个变量的比值，是本节课的关键。课始，采用学生喜欢的猜拳游戏引入，为“两种相关联的量”进行思维预热。接着，选择6个具有较强对比性的学习素材，让学生判断每份材料中的两种量是否相关联。学生在比较、反思中逐步发现，“相关联”的概念还是比较宽泛的，无论是变化方向相同还是变化方向相反，只要是一个量变化，另一个量也随着变化，这样的两个量就是相关联的量。学生在研究变化规律时发现，有的是比值一定，有的是乘积一定，有的是和一定，有的是差一定，从而在对比中主动确定研究的方向，总结出成正比例的两个量在变化过程中的不变为比值一定。

（二）“变”中思“不变”：多元表征，建构正比例的模型

函数有三种数学表示方法：表格、解析式和图像。本课的教学从表格和列式切入，对数量关系进行抽象的梳理，从中认识常量和变量的主要特征，并概括出变量关系的共同特征。学生学习两个现实情境中的正比例关系之后，教师通过富有启发性的问题，引导学生比较、提取共同的本质：都有两种相关联的量，对应数量的比值不变，都成正比例关系。在此基础上，引导学生学习用解析式符号表征正比例关系，从而在抽象层面认识正比例关系的本质。而练习再次联系生活，结合相似图形，孕伏呈现函数图像。多元表征，让概念更加饱满丰盈。

（三）“变”中知“不变”：操作体验，体会正比例的图像

“正比例的图像”主要是下一课时的教学内容，而本节课的练习环节，通过水的体积和高度，引导学生将相对应的点连起来，初步感知正比例的图像呈一条直线。引入图像，更能让学生在数形结合中体验变与不变的函数思想、一一对应思想、极限思想等，同时也为下一课时的学习做了铺垫。在學生认识各点含义的基础上，引导学生连点成线，体验正比例图像的形成过程，让正比例关系的内涵 “看得见”。教学时，可从“往大”和“就小”两个方面追问：比图中时间更大的点还有吗？比图中路程更小的点呢？引导学生更好地感知符合不变规律的“每组数”的无限性，在图像的延伸中使正比例的内涵“看得清”。这样，学生初步认识到两个数量的正比例关系既可以通过具体的数据体现出来，也可以通过直观的图像表现出来。从正比例的图像再回头看正比例的意义，无疑更能加深学生对正比例意义的理解，使学生从具体形象的静态认识，上升到动态建构的过程。