基于BAS-BP模型HMCVT换段液压系统故障的诊断方法
2023-05-29王家博张海军赵余祥刘永华肖茂华鲁植雄王光明
王家博,张海军,赵余祥,刘永华,肖茂华,鲁植雄*,王光明
(1.南京农业大学工学院,江苏 南京 210031;2.江苏农林职业技术学院,江苏 句容 212400;3.山东农业大学机械与电子工程学院,山东 泰安 271018)
液压机械无级变速器(hydro-mechanical continuously variable transmission,HMCVT)是一类新型动力传动形式,主要由液压调速机构、机械变速机构、换段液压系统、冷却润滑系统、控制系统等组成。HMCVT操作简易,不仅满足大功率拖拉机在各类实际工况下的速比变化要求,还提高了燃油利用率,有力推动了大功率拖拉机的智能化快速发展。换段液压系统是HMCVT顺利完成换段的关键,其液压故障发生频率远高于机械故障[1-3]。
国内外一些学者对HMCVT换段液压系统故障类型分析进行了相关研究,采用的故障识别方法可以归纳为故障树专家系统[4]、支持向量机[5]、核方法[6]、BP(back propagation)神经网络[7]等。
BP神经网络容错能力较高且具有较强的泛化能力,因此在求解内部机制繁杂的问题上应用广泛,但由于其对初始的网络权重敏感度较高,容易收敛于局部极小值。为解决其在HMCVT换段液压系统故障诊断方面的不足,将天牛须搜索(beetle antennae search,BAS)算法应用到BP神经网络的权重优化中,建立改进型BP神经网络模型。然后以自主研发的HMCVT为试验平台,通过试验得到5种油路状态模式数据集。基于建立的BAS-BP模型对HMCVT换段液压系统的5种油路状态进行模式识别研究,以弥补以往研究的不足。

图1 3层BP神经网络Fig.1 Three layer BP(back propagation)neural network
1 BAS-BP故障模式识别算法
1.1 BP神经网络原理
BP神经网络主要由输入层(X1,X2,…,Xn)、输出层(Y1,Y2,…,Yn)和隐含层构成,如图1所示。通过反向传播算法变更网络的权值和阈值,在不需要表达映射关系的数学方程式前提下就能获取输入和输出的映射关系[8]。当输入层的各神经元接收到样本数据后,隐含层以及输入层中的权值和选取的激活函数就会自行启动并开始演算分析,然后得到对应神经元的输出值,最后将这个数值和期望结果进行比对,就可能会得到2种结果:1)达到了设定的精度要求,则结束进程,成功输出;2)未达到设定的精度要求,就需要利用误差反向传播,再次变更之前的权值和阈值,不断减少输出值和期望结果之间的误差,直到符合精度标准。
1.2 天牛须搜索(BAS)算法原理
天牛须搜索(BAS)算法[9-10]是模仿天牛寻找食物过程的新型智能仿生算法,在多目标函数优化方面表现优异[11]。一般情况下天牛依照捕获到的气味强弱来寻找食物,天牛的长触须捕捉到的气味强度决定了天牛去向,左边触须捕获的气味强度更强则天牛就会向左前进,否则就会向右前进。与遗传算法、粒子群算法相似,BAS算法即使没有具体形式的函数表达式以及相关梯度信息,也能自动完成择优过程,并且其寻优速度相比其他算法有明显提升。

图2 天牛须简化模型Fig.2 Beetle antennae simplification model
采用质点模型来描述天牛,天牛须简化模型如图2所示。
在对天牛须简化模型时,进行了如下假设:
假设1:将天牛肢体作为质心,天牛触须简化为质心两端。
假设2:天牛的步距与触须间隔的比率是固定的常数。其中,设定左右须间隔远的天牛步伐大,左右须间隔近的天牛步伐小。
假设3:天牛飞到下一步后,头的朝向是随机的。

图3 天牛须算法流程图Fig.3 Beetle antennae algorithm flow chart
天牛须搜索算法的操作流程如图3所示。其演算过程如下:
1)对于任意确定维度空间的完善问题,将xl记作左须位置代号,xr记作右须位置代号,x则表示质心坐标,d0是触须间隔。由于天牛头前进方向具有随机性,所以从天牛右须指向左须的矢量方向也是随机的,即可以设定一个随机向量dir=rand(n,1)来表示。简化计算可得:dir=dir/normal(dir);可以得到xl-xr=d0×dir;显然,xl、xr可以表示成质心的表达式:
xl=x+d0×dir/2
(1)
xr=x-d0×dir/2
(2)
2)对于待优化函数f,求取左右两须的值:fleft=f(xl);fright=f(xr);判断2个值大小。
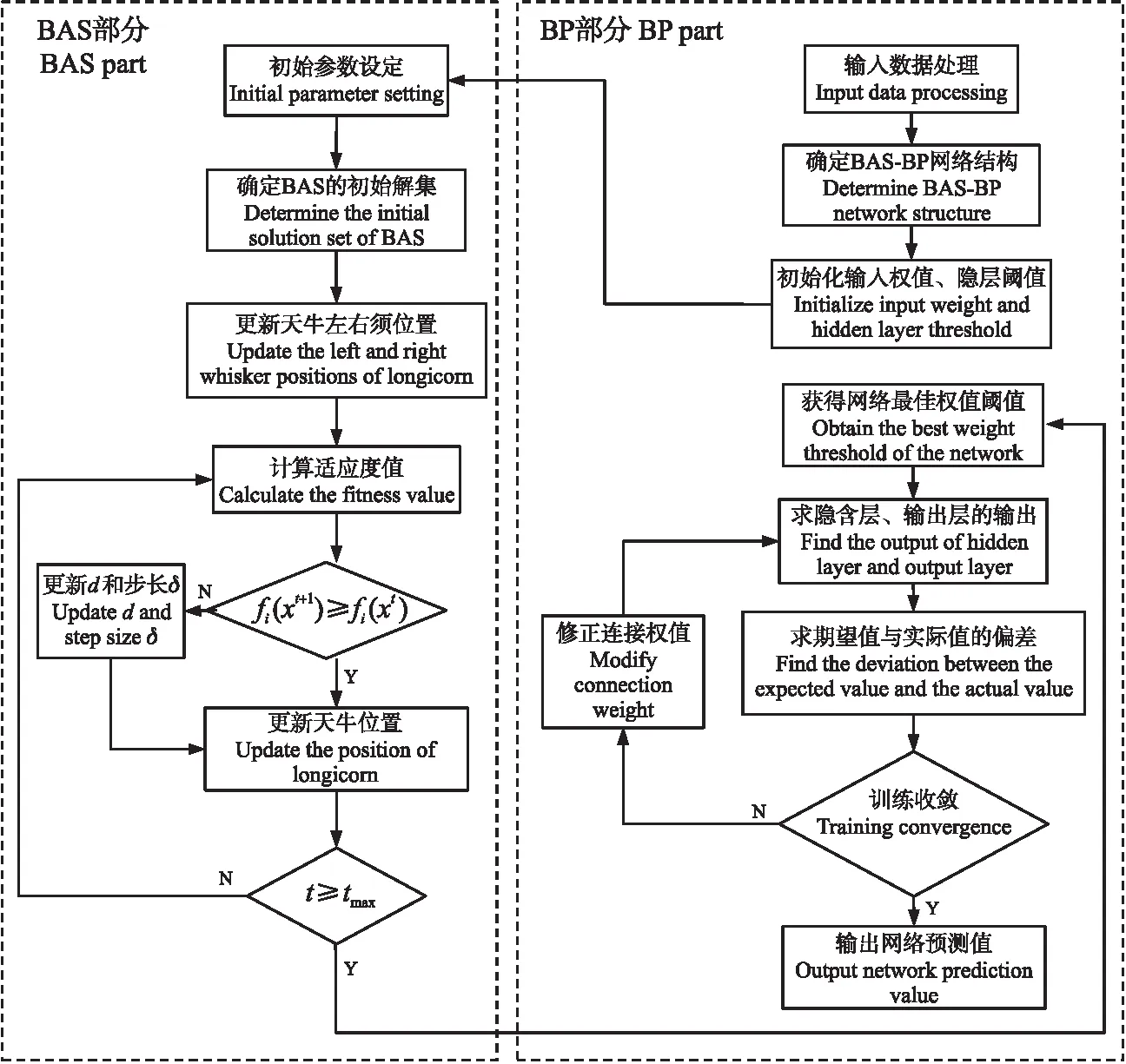
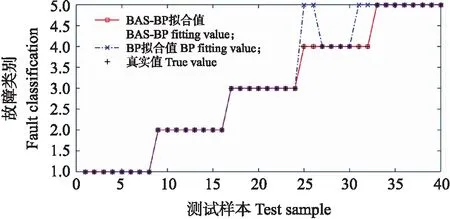
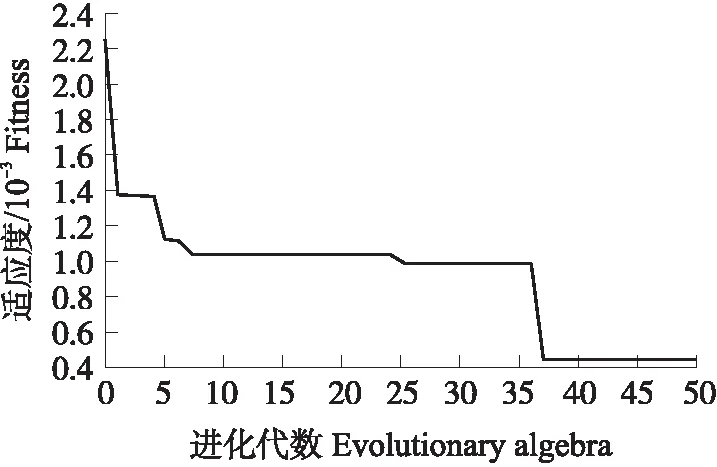
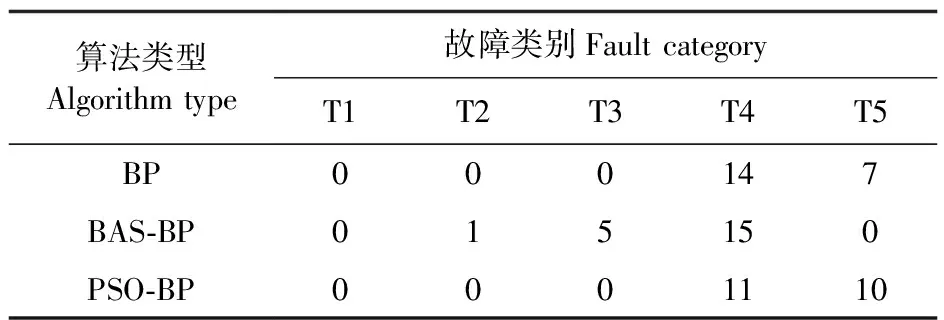
当fleft x=x+step×normal(xl-xr) (3) 当fleft>fright时,要求f的最小值,则天牛向着右触须方向前进距离step,即 x=x-step×normal(xl-xr) (4) 上述2种情况可以采用符号函数sign统一为: x=x-step×normal(xl-xr)×sign(fleft-fright) =x-step×dir×sign(fleft-fright) (5) 式中:normal为归一化函数。 要建立整个从n维到m维的函数对应关系,只需要具备1个隐含层的3层BP神经网络。BP神经网络算法本质上就是一种单点搜索算法,其主要是通过误差函数梯度下降的方式来实现,因而在全局搜索优化方面弊端较多。天牛须搜索算法的原理通俗易懂,兼有所需调整参数少、不依赖梯度信息、操作简易、高效等特点。 天牛须搜索算法改进神经网络的方式就是利用天牛须搜索算法优异的整体搜寻能力,优化神经网络初始权值和阈值,同时基于BP算法不断调整神经网络起始设定的权值以及阈值,最终得到优化的神经网络。其具体流程如图4所示。 图4 BAS-BP神经网络算法流程Fig.4 The flow chart of BAS-BP neural network algorithm 为验证该神经网络的实际效果,需要采集HMCVT换段液压系统的运行数据,试验数据来源于自主研发的液压机械无级变速器试验台[12-13],如图5所示。液压机械无级变速器一共有5个工作段位,包含1个液压起步段及4个液压机械段。在额定转速下,拖拉机的速度能够在4~50 km·h-1实现连续无级变化,HMCVT试验台的测试原理见图6。 图5 HMCVT试验台架结构Fig.5 The structure of the HMCVT test bench1.柴油发动机 Diesel engine;2.变速器前转速转矩仪 Front speed and torque meter of transmission;3.变速器 Transmission;4.液压定量马达 Hydraulic quantitative motor;5.液压变量泵 Hydraulic variable pump;6.变速器后转速转矩仪 Rear speed and torque meter of transmission;7.加载器 Loader;8.测控平台Measurement and control platform;9.换段液压控制系统 Section change hydraulic control system. 图6 HMCVT试验台架测试原理图Fig.6 Schematic diagram of HMCVT test bench 图7 换段液压系统原理图Fig.7 Schematic diagram of shift hydraulic system1.离合器油缸 Clutch cylinder;2.支油路压力传感器 Branch oil circuit pressure sensor;3.调速阀 Speed regulating valve;4.电磁阀 Solenoid valve;5.流量传感器 Flow sensor;6.主油路压力传感器 Main oil circuit pressure sensor;7.齿轮泵 Gear pump;8.滤清器 Filter;9.油箱 Oil tank;10.可调节流阀 Adjustable flow valve;11.齿轮润滑 Gear lubrication;12.节流阀 Throttle valve;13.离合器润滑 Clutch lubrication;14.溢流阀 Overflow valve. HMCVT中的液压油路可以调控变速器输出转速大小及传动比,其中关键部分是湿式离合器及其油路系统[14-16]。湿式离合器的控制是通过控制其液压油路的通断以及冷却油道的充油来实现。HMCVT中的4个湿式离合器用于液压机械工作段,1个用于纯液压工作段上,其油路控制的原理图如图7所示。 图8 换段液压控制系统Fig.8 Clutch oil circuit control system1.电机 Motor;2.油泵 Oil pump;3.单向阀 Check valve;4.溢流阀 Overflow valve;5.流量传感器 Flow sensor;6.压力传感器 Pressure sensor;7.调速阀 Speed regulating valve;8.电磁阀 Solenoid valve;9.集成阀板 Integrated valve plate. 依据上述原理搭建了HMCVT换段液压系统试验装置,如图8所示。换段液压油路系统中,集成阀板上安装了5个电磁阀,用于切换湿式离合器压力油的连通和分离,完成换段过程;电机起到推动油泵进行送油的作用,溢流阀用于调控离合器中油道油压;为了监测湿式离合器结合或相离过程中产生的油压波动,在离合器油道中安装了压力传感器(NS-F压力传感器);调速阀用来调控5个离合器的进油量;同时在主油道中安装了流量传感器(LWGB-4涡轮流量传感器)用来监测离合器结合与分离时液压油实时状况。 HMCVT换段液压系统故障类型基本分类为5种油路模式[17-18],分述如下: 1)一般模式T1:换段液压系统各项指标都符合标准,换段顺畅。 2)离合器活塞不能移动T2:出现这种情况时离合器会处于滑动摩擦状态,摩擦较轻者可以完成换段但却会出现打滑加速现象,摩擦较严重者则会直接破坏离合器。 3)接头处密封圈发生损坏T3:油路发生油道内部的局部泄漏,在充满油时油道内油压不易形成。当油路液压油充足时,该故障对换段油压的作用减小,降低变速器的换段效果。 4)调速阀出口油道堵塞T4:堵塞造成离合器进油量降低,使得相邻摩擦片滑动摩擦时间过长,既降低了换段效果,又可能造成动力不足和离合器损坏的后果。并且该故障模式是渐进式发生,难以察觉。 5)支油路管道接头泄漏T5:与T3存在区别,这类故障通常发生在油路管道接头处,并且油道正在发生局部外泄漏。油压虽然可以正常形成,却会使离合器支油路的压力下降,还有可能掺入空气,在循环过程中液压油会因此产生气穴和振动现象,最终影响变速器的换段效果。 上述故障情况中,T1模式无需纠正。基于文献[19],将换段时的主油路压力设定为4 MPa,调速阀流量标准设定为5 L·min-1;T2模式可利用硬纸板或砂纸填充离合器轴向间隙,模拟不能复位的故障情况;T3模式可以利用已破损的密封圈模拟故障进行试验;T4模式采用手动调节限制调速阀流量进行模拟;T5模式通过放松管道接头以获取要求样本。 换段试验采集到的液压系统压力和流量等原始数据规模庞大,难以参与故障模式识别计算。故利用以下统计量获取其特征属性: (6) (7) (8) (9) (10) (11) 式中:Xf为流量均方根值;Cf为峰值因子;Kf为峭度因子;If为脉冲因子;Sf为波形因子;Xp为压力统计量;xfi、xpi分别为流量、压力在第i个采样点获得的数据;Nf、Np分别为流量、压力的采样点总和数量。 考虑到数据计算的客观性与对比性,本试验在获取统计量数据时,开始点选取为控制单元发出指示后的第一个采样点,结束点选取为开始点后经过1 s的采样点,即数据集以时间长度为衡量单位。按照这一计量方式计算得到了120组故障数据的特征属性样本集。由于实际运行情况下存在多类故障并发的情况,因此故障诊断系统应具有较强的组合故障诊断能力,因此本试验再增加21组T3与T4组合故障模式试验作为组合故障样本,并依照前述规定得到其特征属性并获取了样本集,方便后续对换段液压系统的组合故障模式进行探索研究。 对于一个3层的BP神经网络,输入层、隐含层与输出层的神经元数决定了其结构。由于是以换段液压系统的流量和压力的故障信号为特征向量,对应的换段液压系统的工作状态为输出特征,因此选定输入层神经元数为6,输出层神经元数为1。 在各类研究中对隐含层中神经元数的选取还没有统一的规定。但大致可以通过下列公式确定隐含层神经元数。 N=2n+1 (12) (13) N=log2n (14) 式中:N为隐含层神经元数;n为输入层神经元数;m为输出层神经元数;a为从1到10的常数。 在数次神经网络训练后,选定隐含层的节点数为10。 BAS算法本身要求设定的2个参数,一个是左右须的间隔d,另一个是步距与左右须间隔的比率常数c,试验取d=1,c=5。同时为了增强对整体区域的搜索,试验选择以被测数据的均方误差MSE作为适应度考察函数。公式为: (15) 式中:N为训练集样本数量;xsim(i)为第i个样本的模型输出值;xi为第i个样本的实际值。 由此在算法迭代停止时得到的适应度最小函数值所对应的位置即为最佳解。建立的BAS-BP神经网络框架包括输入层、隐含层及输出层各1个,其中输入层、隐含层、输出层的节点数分别为6、10、1,隐含层激活函数使用正切函数,输出层激活函数使用线性函数。BAS算法搜索空间区域的维度则为81。 以120组单一故障类型样本及21组组合故障类型样本为总研究样本,在120组单一故障类型样本中选出80组样本作为训练集,40组作为测试集,由于是随机选择,所以会产生不一样的试验结果。但这种选取方式可以有效排除样本偶然性,有利于样本数据较少的试验得出更合理的结论。 选择分类正确率(A)、分类准确率(P)和相对误差(Ei)3个评价指标来评价模型的性能,其计算公式如下: (16) (17) (18) 式中:X为故障分类正确总数;Xt为t故障分类正确数;Nt为t故障数;n为样本数;x′i为第i个样本的所属类别预测值;xi为第i个样本的所属类别真实值。 计算所得的相对误差越小代表模型的性能越优。图9和图10分别显示BP神经网络和BAS-BP神经网络模型在训练集上的拟合结果和在测试集上的分类结果,从图可见,BAS-BP神经模型拥有更好的拟合性与分类效果。由图11可见,BAS-BP模型大致需要进化代数达到37能得到最佳解,收敛速率快。 图9 BP与BAS-BP神经网络训练集拟合曲线Fig.9 Fitting curve of BP and BAS-BP neuralnetwork based on training set 图10 BP与BAS-BP神经网络测试集分类曲线Fig.10 Classification curve of BP and BAS-BP neuralnetwork based on test set 图11 BAS-BP神经网络的适应度曲线Fig.11 Fitness curve of BAS-BP neural network 为了测试BAS-BP神经网络模型是否较其他智能优化算法模型在HMCVT换段液压故障诊断方面的优越性,选择PSO-BP神经网络模型从分类正确率、分类准确率、相对误差均值以及迭代过程中CPU运行时间4个维度对模型的性能进行对比。从表1可以看出,BAS-BP模型的训练集与测试集的分类正确率与准确率均强于PSO-BP模型;对于误差精确度,虽然PSO-BP模型与BAS-BP模型差距较小,但BAS-BP模型的训练速率更快。因此,从全局的分类效果与收敛速率上分析,BAS-BP模型性能更好,这也说明BAS-BP模型在HMCVT换段液压系统故障诊断方面更适用。 表1 不同模型效果对比Table 1 Comparison of different models 表2 T3×T4组合故障样本的归类结果Table 2 Classification results of combined fault samples 为考察多种故障并发时BAS-BP模型的实用性,针对试验获得的21组油道堵塞与密封圈破损的组合故障(T3×T4)样本集,分别使用BP、BAS-BP与PSO-BP模型进行直接判别,分类情况如表2所示。 从表2可以看出,BAS-BP模型将21组T3×T4组合故障样本分别归类到T2(4.76%)、T3(23.81%)和T4(71.43%)3种故障模式之中,且算法归类到T3与T4故障模式的占比达95.24%;BP与PSO-BP则将T3×T4的组合故障归类到T4与T5故障模式中,二者均倾向于归类到T4故障模式,分别为BP(66.67%)和PSO-BP(52.38%),原因是组合故障T3×T4与其中T4故障模式较为类似,但经验稀缺(没有对组合故障样本数据深入了解),因此,仍有将其误判为二者以外其他故障模式的可能性。该结论显示当多故障同时发生的情况下,BAS-BP方法可以在没有训练的情况下对组合故障进行有效的诊断识别。 针对液压机械无级变速器换段液压系统进行了试验平台的搭建,在此基础上提出了换段液压故障诊断的BAS-BP方法,采用天牛须搜索算法进行完善,并从分类结果和收敛速率等方面与传统的BP神经网络模型和粒子群算法优化的BP神经网络模型进行了对比分析,获得如下结论: 1)对于液压机械无级变速器换段液压系统的故障诊断,采用模拟故障类型以及传感器反馈的主油路流量和支油路压力数据的方法是有效的。 2)天牛须搜索算法对于初始权值和阈值的优化明显强于一般情况下的BP神经网络,补足了BP算法受限于局部最优的短板问题,且迭代速度快于粒子群优化算法,速率提升85.76%。 3)提出的BAS-BP方法可以高效分析识别液压机械无级变速器换段液压系统的典型单一故障工况,观察对比试验获得的40组试验数据,算法对5种故障模式的分辨率均可达到100%,且在120组任意样本的测试中,算法对5种典型单一故障模式的分辨率分别为100%、100%、97%、100%、100%,体现出较高的稳定性,与PSO-BP方法相比,分类效果更好。 4)建立的基于BAS-BP的神经网络模型可以在不接受训练的情况下对组合故障进行有效分辨,以T3×T4的组合故障识别为例,其识别准确率高达95.24%。1.3 BAS-BP神经网络模型建立
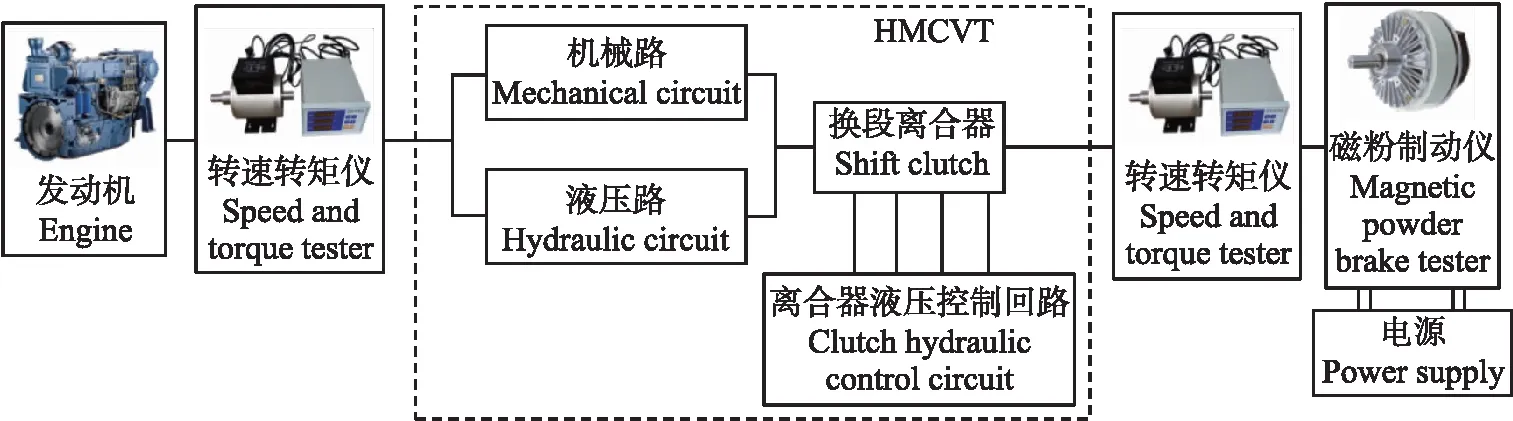
2 试验台及数据来源
2.1 HMCVT试验台

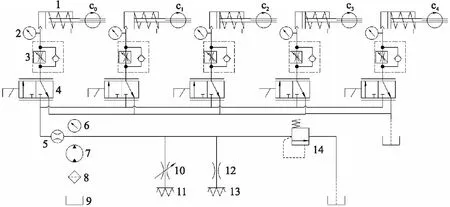
2.2 换段液压系统试验台

3 训练与测试样本集获取
3.1 故障模式类型及其模拟
3.2 特征属性计算
4 BAS-BP神经网络模型性能试验
4.1 BAS-BP神经网络模型结构参数确定
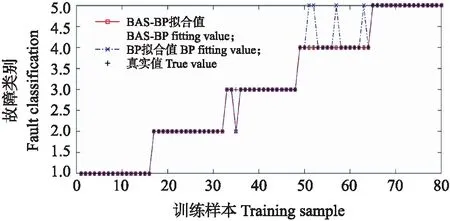
4.2 试验结果与分析

5 结论
