基于GWQPSO-SVM的水产养殖水总磷软测量系统设计与试验

周俊博,蒋冬,肖茂华*,朱虹,汪小旵,陈爽

(1.南京农业大学工学院,江苏 南京 210031;2.江苏省农机具开发应用中心,江苏 南京 210017;3.江苏双木测控技术有限公司,江苏 镇江 212300)

水产养殖对国民经济有重要影响,其水体环境安全直接决定水产品品质[1-2]。而水产养殖水体环境的维护离不开对其水质参数的监测与调控[3-4]。总磷是引起养殖水质富营养化及影响鱼类健康的关键水质参数[5],因此有必要开展水质总磷监测。国外水产养殖总磷监测技术较为成熟,例如,德国WTW公司研制的TresConP511总磷在线分析仪、OP510总磷分析模块等。但这些设备制造成本、运维成本普遍较高,难以在我国水产养殖中普及。

随着人工智能技术的成熟,旨在降低测量成本的机器学习软测量方法已被广泛应用于水质参数监测与预测中。梁萍[6]利用改进蚱蜢算法(improved grasshopper optimization algorithm,IGOA)优化的RBF(radial basis function)神经网络对A水库的总磷含量进行预测;范振[7]采用梯度提升决策树(gradient boosting decision tree,GBDT)算法对蟹塘养殖水体的总磷含量进行预测。但GBDT算法在训练过程中易出现过拟合现象,同为机器学习算法的支持向量机(SVM)具有结构简单、鲁棒性好及广义性强等诸多优势,因此有部分学者将SVM应用于水质监测与预测中。Haghiabi等[8]采用SVM模型对Tireh河的水质参数进行预测,并验证了模型的可行性。

SVM中核函数参数c和惩罚因子g是决定SVM性能的重要参数,但以往2个参数常常依靠人为选取,人的主观臆断会引起SVM过拟合和欠学习现象[9]。种群算法由于易实现、效果好等优点被广泛应用于参数寻优中,如,葛娇娇[10]采用粒子群(particle swarm optimization,PSO)优化最小二乘支持向量机(least squares-support vector machine,LS-SVM)的方法对呼兰河流域的水质参数进行监测,验证了种群优化算法在水质监测应用的可行性。虽然种群算法具有一定寻优效果,但其存在易陷入局部最优解、寻优精度较低等缺陷[11-12],因此单种群算法仍有较大的改进空间,胡洋洋[13]分别采用改进PSO、改进灰狼优化算法(grey wolf optimization,GWO)优化SVM的方法对珍珠贝循环水养殖水质进行预测,试验结果表明,相比于未改进的PSO、GWO算法,该方法的预测效果更佳。

基于以上现状,本文设计了基于灰狼量子粒子群-支持向量机的水产养殖水质监测系统。首先,确定系统的总体设计方案,开发水质监测程序;其次,设计GWQPSO算法,据此提出GWQPSO-SVM总磷软测量模型;最后,基于南京通威水产科技有限公司的养殖水塘水质数据对GWQPSO-SVM总磷软预测模型进行试验验证,旨在为水产养殖总磷浓度实时监测提供一种高精度、低成本的方案。

1 水质监测系统设计

1.1 系统总体设计方案

水质监测系统由传感器组[14-15]、STM32F103核心处理器、ESP8266WIFI无线通信模块、上位机(手机用户端)等组成,总体结构组成如图1所示。STM32F103核心处理器以对应I/O接口采集传感器的信号值,通过A/D转换后得到传感器采集的数据,随后采用ESP8266WIFI无线通信模块进行数据推送[16],通过TCP/IP协议与上位机建立稳定的数据连接进行数据传输[17]。上位机接收传感器组数据并显示,同时执行GWQPSO-SVM模型可实现对水质总磷的软测量。

图1 水质监测系统总体结构图Fig.1 General structure of water quality monitoring system

1.2 数据处理模块设计

1.2.1 硬件模块设计系统通过传感器组对水质数据进行采集。由于本文采用软测量方式确定水质总磷数据,需通过分析与总磷具有相关性的其他水质参数来确定系统传感器组参数选型。

总磷含量升高会导致水产养殖水体富营养化,以藻类为主的水生生物大量繁殖,分解产物大量增加,导致氨氮量增加,由此水质中的氨氮与总磷具有相关性[18];水体温度及溶解氧会影响水质微生物中聚磷菌的酶促反应速率,会引起水体总磷含量变化,由此水体温度及溶解氧与总磷具有一定的相关性[19-20],pH值的变化会影响水体藻类的繁殖能力,过高的pH值会对藻类的光合作用产生抑制作用,而藻类生长量的削减可引起水体总磷含量的降低,因此pH值与总磷也具有相关性[21]。基于此,本文选择水温传感器、pH传感器、溶解氧传感器、氨氮传感器作为本系统的传感器组,各传感器的参数信息如表1。

表1 传感器及其参数Table 1 Sensors and parameters

在实际检测水质数据采集中,采集终端会通过对应的传感器节点将调理信号传输至中央处理器处理,通过CPU计算后数据保存至下位机的存储器中,水质数据处理模块硬件布置方案如图2所示。

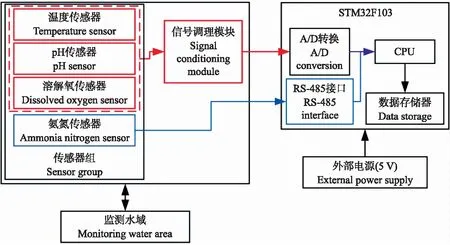
图2 水质数据处理模块硬件布置方案Fig.2 Hardware arrangement scheme of water quality data processing module

图3 数据采集节点软件设计流程Fig.3 Flow chart of data acquisition nodesoftware design

1.2.2 软件模块设计系统的数据采集节点软件部分通过Keil5软件编写,当下位机供电后,终端节点进行初始化,当终端节点成功初始化后,调用数据采集程序获取传感器数据并进行数据封装存储。为实现数据传输节点与上位机的通讯,本系统选用ESP8266WIFI模块,通过TCP/IP协议与上位机建立稳定的数据流连接进行信息交互,数据采集节点相关的软件设计流程如图3所示。

系统WIFI无线通信软件使用STA模式进行开发,基于此模式下,将WIFI无线通信模块连入对应网络,通过TCP/IP协议连接服务器从而实现数据的传输,WIFI无线通信模块软件设计流程如图4所示。

1.3 服务器交互端设计

本文选用MySQL作为数据库与服务器进行交互,同时为减小MySQL的查找压力,采用Redis提供缓存服务。首先,创建包含表现层(Controller)、业务层(Service)、持久层(Dao)的3层服务器架构,如图5所示;其次,通过API持续监控下位机无线通信的IP地址,在项目中创建Socket通道从下位机中持续获取传输的水质检测数据,并将接收到的数据更新到MySQL数据库中;最后以WePY框架和JavaScript的语法编写系统前端,采用JavaScript语法编程将对应的数据嵌入在前端页面中,在前端页面中使用WePY框架来完成请求发送与数据获取。

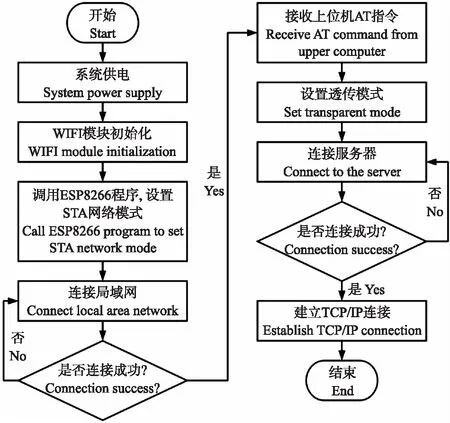
图4 WIFI无线通信模块软件设计流程Fig.4 Flow chart of software design WIFIwireless communication module

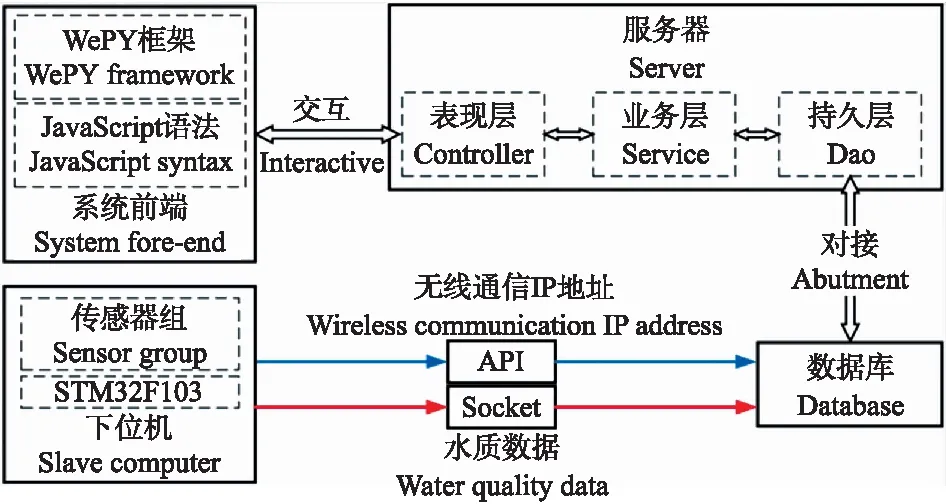
图5 服务器交互端设计流程Fig.5 Flow chart of server interactive design

系统前端的手机水质监测程序采用微信开发者工具进行开发。从图6可见,该程序主要由账号管理部分与水质监测部分组成,账号管理部分包括账号注册、账号登录以及修改密码功能,水质监测部分包括监测地点天气显示、各传感器数据实时显示、总磷数据显示以及水质预警功能。

图6 水质监测程序界面Fig.6 Interface of water quality monitoring procedure

2 基于GWQPSO-SVM的总磷软测量方法

2.1 支持向量机(SVM)

SVM是一种基于统计学习理论的机器学习算法,其原理为在进行样本分类时确定离2类样本距离最大的超平面[22-24]。SVM利用内积核函数代替向高维空间的非线性映射,避免了传统机器学习模型维数灾难和过拟合的问题,在处理复杂关系数据和数值预测等方面具有巨大优势。虽然水体温度、水体pH值、溶解氧含量、氨氮含量与总磷间存在一定的相关性,但5个指标间的具体关系较为复杂,因此选用SVM作为总磷软测量模型。

2.2 GWQPSO算法

SVM中核函数参数c和惩罚因子g对模型的泛性能有很大的影响[25-26]。种群由于具有优良的收敛性能和寻优精度被广泛应用于参数寻优。本文结合PSO算法和GWO算法2类种群算法,借此提出GWQPSO算法优化的SVM参数c和g。

个体速度更新公式为:

(1)

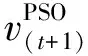
个体位置更新公式为:

(2)

GWO算法基本原理效仿自然界灰狼群的社会等级制度和狩猎策略的新型种群算法[28]。将狼群分为α、β、γ、δ种群,狼群δ中个体在狩猎过程中接受狼群α、β、γ中个体的支配。GWO算法的过程可分为包围、追捕、攻击3个阶段[29]。为方便表示,狼群中个体总数、总迭代次数、个体目前迭代次数的设置同PSO算法。

灰狼个体猎物包围方式为:

(3)

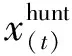
灰狼个体猎物追捕方式为:

(4)

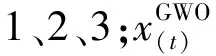
灰狼个体攻击猎物方式为:当|A|<1时,狼群认为该猎物为最优解,狼群开始攻击猎物,向最优解靠拢;当|A|≥1时,狼群远离猎物,狼群重新在全局寻找最优解。

PSO算法收敛速度快,但也存在易过早收敛、易陷入局部最优等缺点,而GWO算法具有较强的全局收敛能力[30-32]。由此,本文将2种算法融合:采用GWO算法更新群内个体位置,利用GWO算法中狼群社会等级制度增强群内个体交流,增强算法的寻优效率与全局寻优能力;通过PSO算法赋予群内个体速度,使其拥有局部搜索能力,提高个体寻优精度。同时,为克服个体速度位置连续变化引起的个体搜索范围有限的缺陷,采用QPSO算法的思想对PSO算法的位置更新方式进行改进,进而提高算法的寻优范围。基于此,本文提出一种GWQPSO算法。

GWQPSO算法个体速度公式为:

(5)

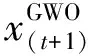
GWQPSO算法个体位置公式为:

(6)

式中:x(t+1)为GWQPSO算法更新后个体位置;pkb为第k个个体当前最优解。

GWQPSO-SVM模型算法流程如图7。

图7 GWQPSO-SVM模型算法流程Fig. 7 Flow chart of GWQPSO-SVM modelSVM:支持向量机Support vector machine;GWQPSO:灰狼量子粒子群Grey wolf quantum particle swarm optimization;GWO:灰狼优化算法Grey wolf optimization. 下同 The same below.

3 GWQPSO-SVM总磷软测量模型性能试验

3.1 试验方案

试验场地为南京通威水产科技有限公司的养殖水塘,为使GWQPSO-SVM模型能够满足水质监测的实际应用需求,需先采用已有含有总磷的水质数据进行模型训练。训练数据采用公司技术人员采集的2022年4月14日至30日期间总磷、水温、pH、溶解氧及氨氮历史水质数据80组。使用本文水质监测系统的下位机采集水温、pH、溶解氧及氨氮数据55组作为测试数据来软测量水体中的总磷含量,采样点位于养殖水塘中央,测试数据采集时间为2022年5月1日至12日,同时采用公司技术人员于同一时间节点内采集的总磷数据作为GWQPSO-SVM总磷软测量模型测量值的对照数据。

3.2 试验结果与分析

为验证本系统总磷软测量的效果,同时执行SVM模型、PSO-SVM(particle swarm optimization-support vector machine)模型、GWO-SVM(grey wolf optimization-support vector machine)模型、QPSO-SVM(quantum particle swarm optimization-support vector machine)模型、GWOPSO-SVM(grey wolf optimization particle swarm optimization-support vector machine)模型以及本文开发的GWQPSO-SVM模型进行总磷浓度软测量,图8为6种算法的测量结果。

为验证各模型的测量性能,选取绝对误差(absolute error,AE)、平均绝对值误差(mean absolute error,MAE)、平均绝对百分比误差(mean absolute percentage error,MAPE)、均方误差(mean square error,MSE)、均方根误差(root mean square error,RMSE)评价各模型的性能,结果见表2。

各指标计算方式如下:

(7)

式中:S为样本总数;ym为第m个样本的实际输出值;Ym为第m个样本的期望输出值。

图8 采用模型SVM(A)、PSO-SVM(B)、GWO-SVM(C)、QPSO-SVM(D)、GWOPSO-SVM(E)、>GWQPSO-SVM(F)测量水中总磷浓度Fig.8 The total phosphorus concentration in water measured by models of SVM(A),PSO-SVM(B),GWO-SVM(C),QPSO-SVM(D),GWOPSO-SVM(E),GWQPSO-SVM(F)PSO-SVM:粒子群算法-支持向量机Particle swarm optimization-support vector machine;GWO-SVM:粒子群算法-支持向量机Grey wolf optimization-support vector machine;QPSO-SVM:量子粒子群-支持向量机Quantum particle swarm optimization-support vector machine;GWOPSO-SVM:灰狼粒子群-支持向量机Grey wolf optimization particle swarm optimization-support vector machine. 下同 The same below.

表2 不同模型的性能Table 2 Performance of different algorithms

由表2可知,相较于SVM模型,PSO-SVM、GWO-SVM模型的5种误差均有小幅度降低,证明种群算法在优化SVM参数方面的可行性,但从图8-A、B、C中软测量值曲线可知,PSO-SVM、GWO-SVM模型的测量结果与SVM模型较为相近,整体数据值与实际值偏离较大,说明单种群优化算法的优化能力有待提高;QPSO-SVM模型的5种误差相较于SVM模型均大幅度下降,从图8-D可知,相较于PSO-SVM、GWO-SVM模型,QPSO-SVM模型的测量结果与实际值偏离较小,说明改进后种群算法性能更佳;相较于PSO-SVM、GWO-SVM、QPSO-SVM模型,GWOPSO-SVM模型的5种误差皆为最低,验证了复合种群优化算法优越于单种群优化算法的结论;相较于SVM模型,GWQPSO-SVM模型的5种误差分别下降65.70%、65.68%、61.85%、88.16%、65.63%,由表2及对比图8-E、F可知,相比于GWOPSO-SVM模型,GWQPSO-SVM模型的整体数据值更贴近实际值。相比于其他5种模型GWOPSO-SVM的运行时间最短,为3.156 2 s。因此,相较于其他5种模型,GWQPSO-SVM模型具有良好的预测能力及运行效率。

理论来说总磷是一种渐变的化学量,而图8中存在着接近0.4和0的2个数据点,不符合其他样本点总磷数据的渐变趋势。这是由于水质环境复杂多变,水质传感器会发生数据波动,图8中2个异常数据点极有可能为失真数据。由图8-F可知,除去2个异常数据点外,GWQPSO-SVM模型能准确预测其他总磷样本点数据的变化趋势,合理预测出总磷数值。因此本文提出的模型能够有效克服因偶然因素引起的数据波动。

图9 不同算法的适应度曲线Fig.9 Curve of different algorithms fitness

为验证GWQPSO算法的寻优能力,选用SVM训练过程中的MSE作为适应度,PSO、GWO、QPSO、GWOPSO、GWQPSO这5种算法的适应度曲线如图9所示,5种优化算法最优c、g解如表3。

从图9可知,相较于PSO算法,GWQPSO算法收敛时的迭代次数由74下降至9,下降了87.84%;最终收敛适应度由0.081 2下降至0.072 7,下降了10.47%。GWQPSO算法收敛性能为5种算法最佳,这是由于相比于PSO、GWO、QPSO算法,GWQPSO算法采用了GWO、PSO算法相结合的方式,通过GWO算法内等级制度加强群内个体信息交流能力的同时也通过PSO算法的速度更新方式提高个体局部寻优能力,相比于GWOPSO算法,GWQPSO采用了QPSO算法的位置更新方式,克服了群内个体连续变化引起的寻优空间有限的弊端,进一步扩大了个体的寻优范围。由表3可知,GWQPSO算法寻得的c、g最优解分别为0.113 5、2.529 0,结合图9的适应度曲线可知,GWQPSO算法最终收敛适应度为5种算法最低,说明其寻得的c、g最优解最靠近全局最优解。由此,相较于其他4种算法,GWQPSO算法具有良好的寻优能力。

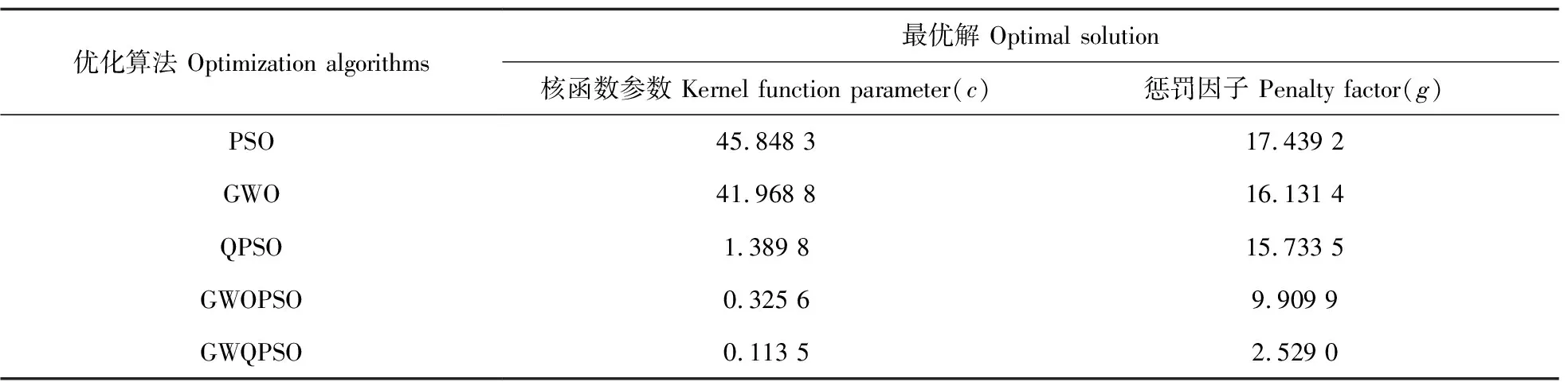
表3 不同算法的最优解Table 3 Optimal solutions of different algorithms

为避免算法随机性导致的试验偶然性,对6个模型再进行4次试验,同样选择AE、MAE、MAPE、MSE、RMSE这5个参数作为衡量模型性能的指标,4次试验结果如表4所示。由表4可知,在同等试验条件下,GWQPSO-SVM模型4次试验的5种误差平均值分别为2.348 0、0.042 7、0.280 2、0.003 6、0.060 2,相较于其他5种模型最低,同时单次试验的5种误差值均较低。综上,GWOPSO-SVM模型无论是在预测能力、寻优能力及模型稳定性方面都具有良好的性能。

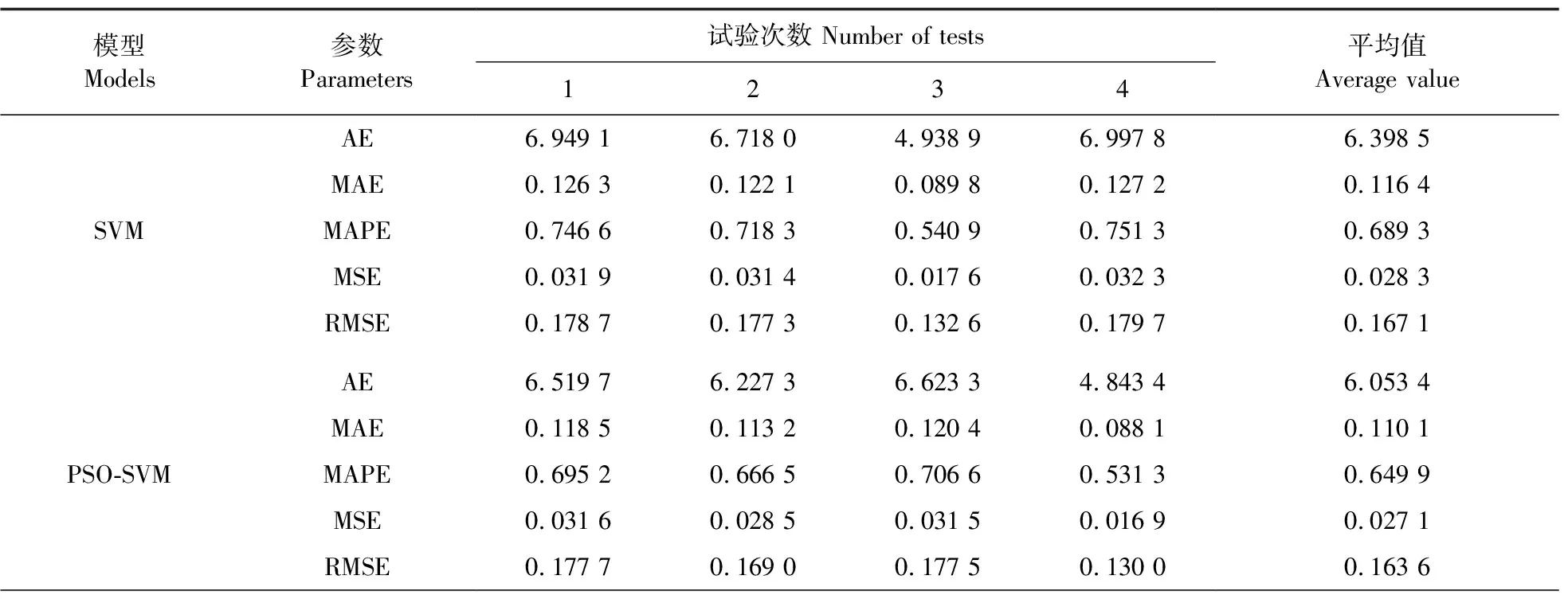
表4 多次试验结果Table 4 Multiple test results

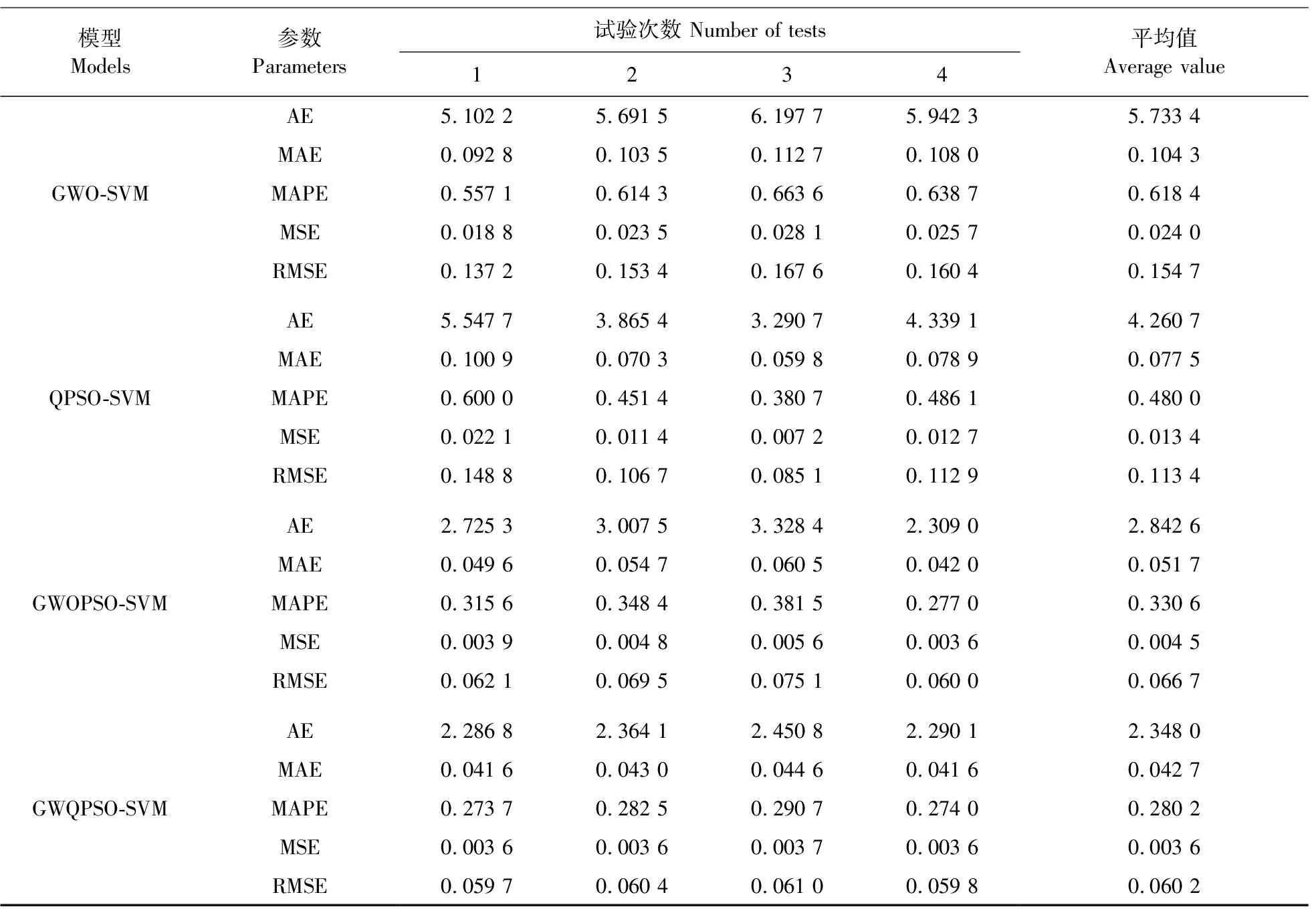
续表4 Table 4 continued

4 结论与讨论

本文针对水产养殖过程中的水质参数监测与预测问题,开展了基于GWQPSO-SVM的水产养殖水总磷软测量系统设计与试验工作,可实现高精度低成本水产养殖总磷测量。但本文的方法具有一定的局限性和改进空间,相关讨论如下:

1)受试验条件及时间的限制,仅采集了水产养殖场4月份的水质数据,时间跨度及数据规模较小。对于水产养殖场而言,水生生物(如海藻、水草、浮游生物等)对水体总磷含量影响较大,同时水生生物的生长状况因季节而异,而一个月内水生生物的生长状况稳定,水质数据的变量变化程度较小,因此本文提出的GWQPSO-SVM总磷软测量系统具有一定的季节性。在后续的研究中,可以通过全季水质数据训练模型,增大水质数据的时间跨度,进一步提高模型的普适性和实用性。

2)本文采用多种算法组合的方式提升优化算法的优化能力,相比于其他已有的组合算法(GWOPSO)具有一定的优越性。但由于采用SVM作为总磷软测量模型,SVM结构简单优化参数较少,因此本文设计的GWQPSO算法存在普适性的问题。在后续研究中应将优化算法与更多机器学习模型融合,同时根据不同机器学习模型的特性制定合适的改进策略,以增强优化算法普适性。