基于解析法的农机轴承转子系统润滑特性分析*

苏来博 ， 李 冰 ， 徐武彬 ， 高宇星 ， 李 铮

（1.广西科技大学机械与汽车工程学院，广西 柳州 545006；2.广西土方机械协同创新中心，广西 柳州 545006）

0 引言

随着现代农业机械的发展，农机设备正向着高负载、高速度、高精度等方面发展，这对设备的整机性能提出了更高的要求。因此，对农机的滑动轴承转子系统的承载能力、运行稳定性以及摩擦损耗等特性进行研究尤为重要[1-5]。

王书茂等[6]基于数值解油膜力针对农机转子特点提出的3级转速多平面矫正法，既简化了挠性转子复杂的动平衡步骤，又提高了转子实际工况的动平衡精度。袁雪鹏等[7]基于数值法研究了制造误差对农机转子系统动力学的影响，但数值法迭代速度慢，使用不够便捷。Jiao等[8]基于数据库法对不平衡转子系统进行了非线性动力学分析，但该方法需不定期更新数据库，普遍性较差。黑棣等[9]基于无限长农机轴承假设研究了柔性转子系统的非线性动力学行为，并利用改进后的Wilson-θ法研究了系统的非线性稳态特性。马晓栋[10]基于无限短农机轴承研究了油膜温度变化对临界转速下系统发生涡动和振荡时对特性的影响。综合上述研究结果发现，无限长、无限短轴承模型不符合实际情况，误差偏大。

因此，基于更加符合实际的有限长农机轴承模型进行润滑特性解析分析具有重要意义，不仅加快了运算速度，也保证了精度。文章将对解析油膜力下的农机轴承运动特性进行分析，为提高转子承载能力、系统稳定性及降低摩擦损耗等方面提供参考。

1 农机转子系统解析油膜力推算

1.1 轴承物理模型及油膜压力分布方程

轴承周向截面图如图1（a）所示，轴承轴向平面视图如图1（b）所示。其中，O为轴瓦中心，Oj为轴颈中心，Rj为轴颈半径，Φ0为位置角，θ为圆周方向坐标，ω为轴颈自转角速度，e为轴颈相对于轴瓦的偏心位移，h为液膜厚度，c为轴承径向间隙，L为轴承宽度，Dj为轴颈直径。

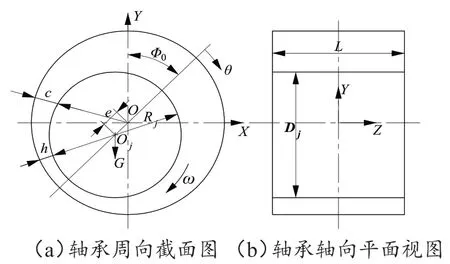
图1 有限长农机滑动轴承动力学模型

假设润滑流体粘度不变，且轴瓦与轴颈间腔体体积固定，轴承流体润滑的Reynolds方程可表示为：

对式（1）进行无量纲化，引入以下无量纲参数：

式中，ps为无量纲油膜压力，H为无量纲油膜厚度，ε为偏心率，λ为无量纲轴向坐标，τ为无量纲时间，ε'为轴颈中心扰动速度，θ'为轴颈周向变化速率。

将式（2）代入雷诺方程式（1），得到无量纲雷诺方程：

无量纲油膜厚度为：

将式（4）代入式（3）并进行推导得到式（5）：

1.2 解析解油膜压力求解

式（5）是关于三角函数的方程式，假设油膜压力分布函数可以拆分为：

式中，pl(θ,ξ)为解析特解，ph(θ,ξ)为解析通解。

通过分离变量可得特解：

以乘法形式分离通解：

将式（6）至式（8）代入式（5）整理得：

由于油膜压力特解满足Reynolds方程，故有：

显然，式（10）是关于变量θ、ξ的函数，通过分离变量法可将其拆分为两个二阶非齐次微分方程：

对式（12）积分可得：

由于该研究将与在Reynolds边界条件下运用有限差分法得到的结果进行比对验证，故该研究为了实现条件统一，将使用Reynolds边界条件。

轴承周向边界条件：

轴向两端边界条件：

设S=0，由已知条件可知，当ξ=λ=±1时，g(±1)=0，故式（13）中的系数为c1=c2=0。设一阶函数Z(θ)为：

则式（11）可表示为：

对式（17）一阶非齐次线性微分方程求解：

对式（18）进行不定积分：

运用Sommerfeld积分变换式求解式（19）：

由周向边界条件可知：θ=θ0=0，φ(θ0)=0，θ=θ1，由条件θ=θ=0，φ(θ)=0，得00到c4：

由条件θ=θ1，φ(θ1)=0，得到c3：

由于θ与α是单映射关系，通过线性插值法求解α1。经过以上推导可得到油膜压力特解pl(θ,ξ)。

油膜压力通解求解：将式（10）代入式（9）的非齐次方程中，可以得到以下方程式。

通过分离变量法可得：

将式（25）拆分可以得到：

设I=-k2，则求解式（26）可得：

把大气压设为0，根据Reynolds边界条件，轴承在两端的压力为0，所以在轴承两端的油膜压力存在以下关系：

通过式（29）可得到轴承两端轴向油膜压力通解：

因此：

轴向油膜压力分布函数求解：根据式（30）边界条件，式（28）中的常数如下式：

将式（32）代入式（28）可得：

将式（31）代入式（24）可得：

与式（11）联立，可得：

通解的表达式为式（36）。

将式（20）与式（36）代入式（6）得油膜压力表达式，即式（37）。

2 算例分析

2.1 油膜压力特解和通解算例

图2（a）、图2（b）分别为位置角Φ0=30°，长径比L/Dj=1，偏心率ε=0.3，x'=y'=0，径向间隙c=0.381 mm，角速度ω=398 rad/s时的轴承无量纲油膜压力特解分布图和通解分布图；轴承基本参数如表1所示。

表1 轴承基本参数

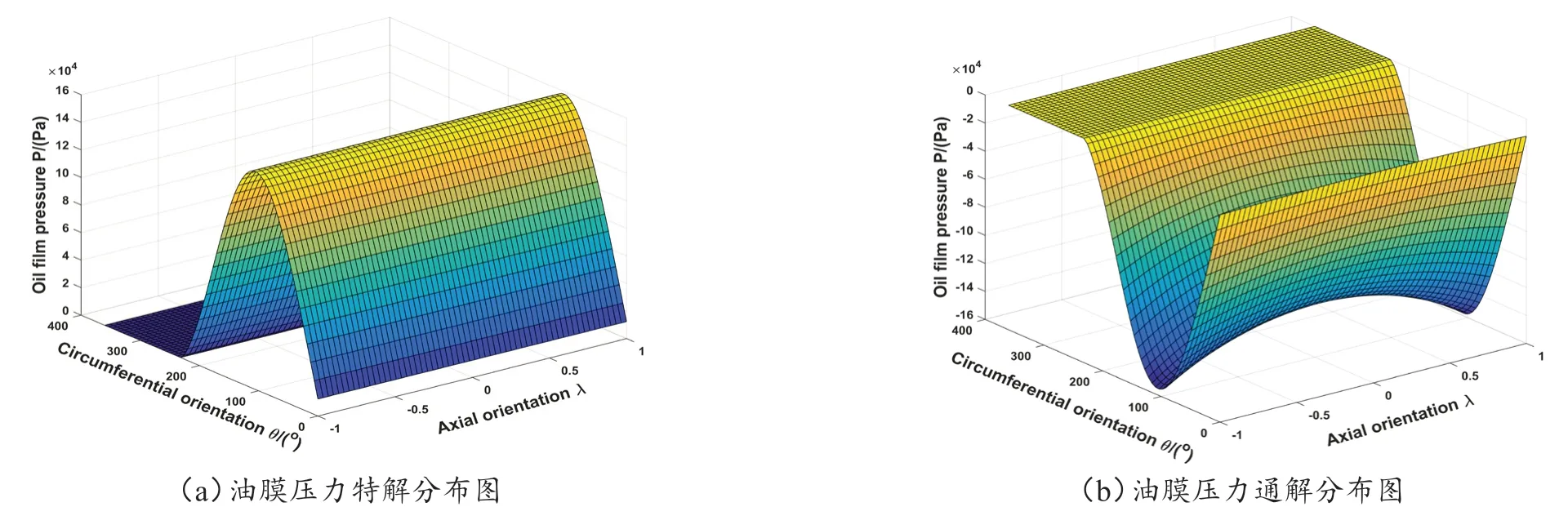
图2 油膜压力特解pl(θ,z)和通解ph(θ,z)分布图

由图2（a）可以看出，油膜压力特解在轴向上是不变的，在位置角为180°时达到最大峰值。由图2（b）可以看出，油膜压力通解在λ=0处呈对称分布，越往轴承两侧压力越小。

2.2 拟合油膜压力特解和通解

位置角Φ0=30°，长径比L/Dj=1，偏心率ε=0.3，x'=y'=0，径向间隙c=0.381 mm，角速度ω=398 rad/s时，全圆瓦轴承无量纲油膜压力分布如图3所示。

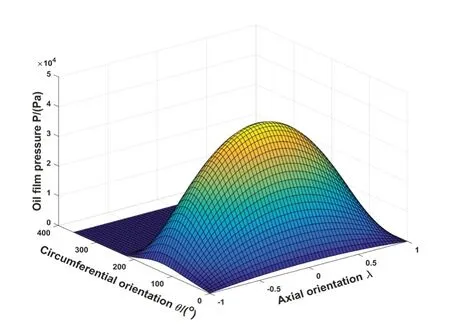
图3 油膜压力p(θ,z)沿周向和轴向坐标上的三维分布图

通过图3可以看出，周向最大油膜压力在θ=90°处，越靠近轴承两端油膜压力越趋于0，且油膜压力梯度在轴承中心处最大。

3 农机转子系统运行特性分析

3.1 转子系统承载特性

Sommerfeld数是用来描述转子系统承载特性的重要参数。当水平安装的系统运行稳定时，油膜压力水平分量Fx=0，通过公式（38）可以得到Sommerfeld数。

式中，μ为润滑油粘度；n为转子转速；L为轴承宽度；Dj为轴颈直径；F为轴承载荷；Rj为轴颈半径。

有限长、无限短、无限长三种农机轴承模型基于解析解油膜力的Sommerfeld数随偏心率变化的对比图如图4所示。可以看出，同等偏心率条件下，无限长轴承模型承载能力最强，其次是有限长轴承模型、无限短轴承模型。随着偏心率的增大，有限长轴承模型的承载能力增大，并且与无限短轴承模型变化的趋势和速率相近。

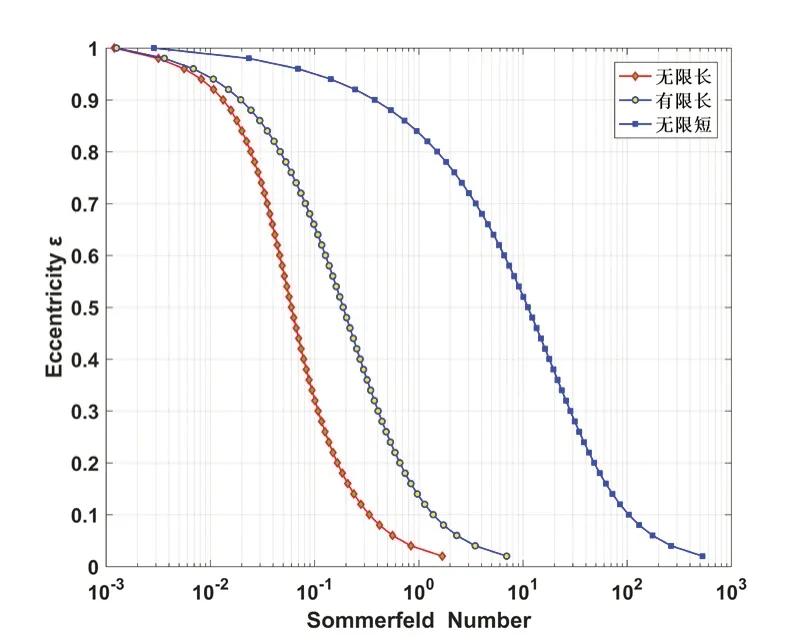
图4 不同农机轴承模型Sommerfeld数与偏心率关系对比

3.2 能量损失特性

滑动轴承转子系统的润滑方式为油润滑，在转子运行过程中，轴瓦和轴颈之间充满油液，所以轴颈和油膜会产生摩擦，具有一定的摩擦功率损耗。滑动轴承转子系统的摩擦损耗对系统的稳定运行和轴承温度的升高有很大的影响。摩擦功率损失计算表达式为：

式中，Ff为轴承摩擦力，Ut为轴颈切向转速，Rj为轴颈半径；L为轴承宽度；ω为转子角速度。

能量损失曲线对比图如图5所示，在偏心率相同的情况下，长径比越大，系统能量损失越大；能量损失随着偏心率的增加而减小。无限短轴承的能量损失几乎为0，这与轴承系统工作情况严重不符，所以不采纳该模型；无限长轴承在整个偏心率范围内能量损失过大，尤其是当偏心率小于0.3时，能量损失急剧上升，所以该轴承模型的润滑特性理论不能应用于实际工程。有限长轴承能量损失变化一直维持在正常水平并趋于稳定，偏心率越小，能量损失越大，故有限长轴承模型的解析润滑特性更加符合实际。

图5 不同农机轴承模型的能量损失特性对比

4 结论

通过Sommerfeld变换、分离变量法以及雷诺边界条件得到了有限长农机轴承的非线性油膜力。并以无限短、无限长、有限长农机轴承模型为研究对象，分析了其在解析油膜力的基础上农机系统的承载特性和能量损失情况。结果表明：同等偏心率条件下，无限长轴承模型承载能力最强，其次是有限长、无限短轴承模型。Sommerfeld数在偏心率在0.3~0.7之间时变化率最低，承载能力稳定。长径比越大，系统能量损失越大；偏心率在0.5~0.7之间时三种模型能量损耗比较稳定，偏心率区间转子运行稳定。通过对比发现，无限长、无限短轴承模型运行特性的误差较大，故不能采用；有限长农机轴承模型解析油膜力更加贴合实际，计算速度快，准确性高，可以为农机转子系统在实际应用中的故障检测提供可靠的理论支持。